数据结构与算法-- 二叉树中和为某一值的路径

二叉树中和为某一值的路径

题目：输入一颗二叉树和一个整数，打印出二叉树中节点值的和为给定值的所有路径。从树的根节点开始往下一只到叶子节点所经过的节点形成一条路径。
我们用二叉树节点的定义沿用之前文章中二叉查找树实现原理定义。如下：

public class BinaryNode implements Comparable {private Object element;private BinaryNode left;private BinaryNode right;private int count;

案例：输入如下图中二叉树和整数22，打印出两条路径，第一条包含节点10， 12，第二条包含10,5，7

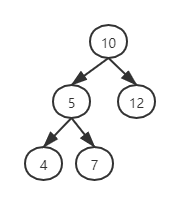
在这里插入图片描述

二叉树的节点定义中，我们是无法得到树的路径这个概念值的，应为二叉树中并没有介绍树的路径的数据结构，因此对于大多数人而言，这个是一个新的理论模型，也就很难一下找到思路，我们从一个案例入手更加简单，还是用上面的案例：
由于路径就是根节点出发到叶子节点，也就是说路径总是以根节点为起点，因此是先根遍历，也就是我们可以用二叉树的前序遍历，根，左，右的遍历方式，在我之前的文章数据结构与算法–二叉树实现原理中详细介绍了三种遍历方式并附带源码，我们以前序遍历为思路解这个问题。
按前序遍历范问上图，10,5，4,7，12 是前序遍历的顺序，我们可以从二叉树结构中看到，没有指向父节点的指针，因此范问5 的时候并不知道10 节点的路径和值，因此我们需要把上一个节点经过的路径保存下来，每次范问一个节点都将当前节点的路径添加到下一个节点的路径中，因此到达5 时候，因存 10，5接着到大4，总和为9 ！= 22.因此返回5节点，到达7 ，和为 10+5+7 = 22 符合提议，接着返回10 ，访问12,10+12 = 22 符合题意，因此有两组解
按如上分析有如下步骤：
- 安前序遍历递归实现二叉树的遍历
- 范问每个子节点之前将本节点走过的路径path和路径和count传递给需要范问的子节点
- 字节点范问之前将父节点路径path添加上自己的路径 path+element，路径和添加自己的节点权重 path+weight
- 如果范问节点没有子节点，则比较路径和count 是否和目标值一致，一致则正解。
- 如下实现，此处构造二叉树的方法沿用之前文章：数据结构与算法–二叉查找树实现原理中方法

/*** 二叉树中查找和为n 的路径** @author liaojiamin* @Date:Created in 10:51 2021/5/17*/
public class FindPathInBinary {public static boolean findPath(BinaryNode binaryNode, Integer target) {List<Integer> list = new ArrayList<>();list.add(Integer.valueOf(binaryNode.getElement().toString()));Integer count = Integer.valueOf(binaryNode.getElement().toString());return findPath(binaryNode, list, count, target);}public static boolean findPath(BinaryNode binaryNode, List<Integer> beforePath, Integer beforeCount, Integer target) {if (binaryNode.getLeft() == null && binaryNode.getRight() == null) {printPath(beforePath);System.out.println("beforeCount：" + beforeCount);if(beforeCount == target){System.out.print("存在路径：");printPath(beforePath);System.out.println();}return false;}if (binaryNode.getLeft() != null) {BinaryNode left = binaryNode.getLeft();Integer count = beforeCount + Integer.valueOf(left.getElement().toString());List<Integer> list = new ArrayList<>();list.addAll(beforePath);list.add(Integer.valueOf(left.getElement().toString()));findPath(binaryNode.getLeft(), list, count, target);}if(binaryNode.getRight() != null){BinaryNode right = binaryNode.getRight();Integer count =  beforeCount + Integer.valueOf(right.getElement().toString());List<Integer> list = new ArrayList<>();list.addAll(beforePath);list.add(Integer.valueOf(right.getElement().toString()));findPath(binaryNode.getRight(), list, count, target);}return false;}public static void printPath(List<Integer> objectList) {for (Object o : objectList) {System.out.print(o);System.out.print(",");}}public static void main(String[] args) {
//        Integer arr[] = new Integer[]{44,94,92,23,42,13,7,76,70,40,78,28,78,36,14,53,10,91,36,15};Integer arr[] = new Integer[]{10,5,4,7,12};BinaryNode node = new BinaryNode(null, null, null);BinarySearchTree searchTree = new BinarySearchTree();for (int i = 0; i < arr.length; i++) {int num = arr[i];node = searchTree.insert(num, node);System.out.print(num+",");}System.out.println();System.out.println();findPath(node, 22);}}