并查集概念

并查集单看名字大家也能猜到这个算法的作用，是用来对集合进行合并和查找操作

并查集是一种树型的数据结构，用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。——来自百度百科

就是将原本不一样的集合，但是由于某种关系有了联系，把他合并成同一个集合，就是实现一个这样的功能。

基本操作

并查集是一种非常简单的数据结构，（我是说它的算法实现简单）它主要涉及两个基本操作，分别为：
A．合并： 合并两个不相交集合
B．查找： 去判断两个元素是否属于同一个集合
接下来，我会用并查集的图形解释来看下如何实现这两个基本操作。
1.可以看到这里有六个小球，他们代表六个不一样的元素，用数组来表示他们，给他们附上值，来代表不一样的集合

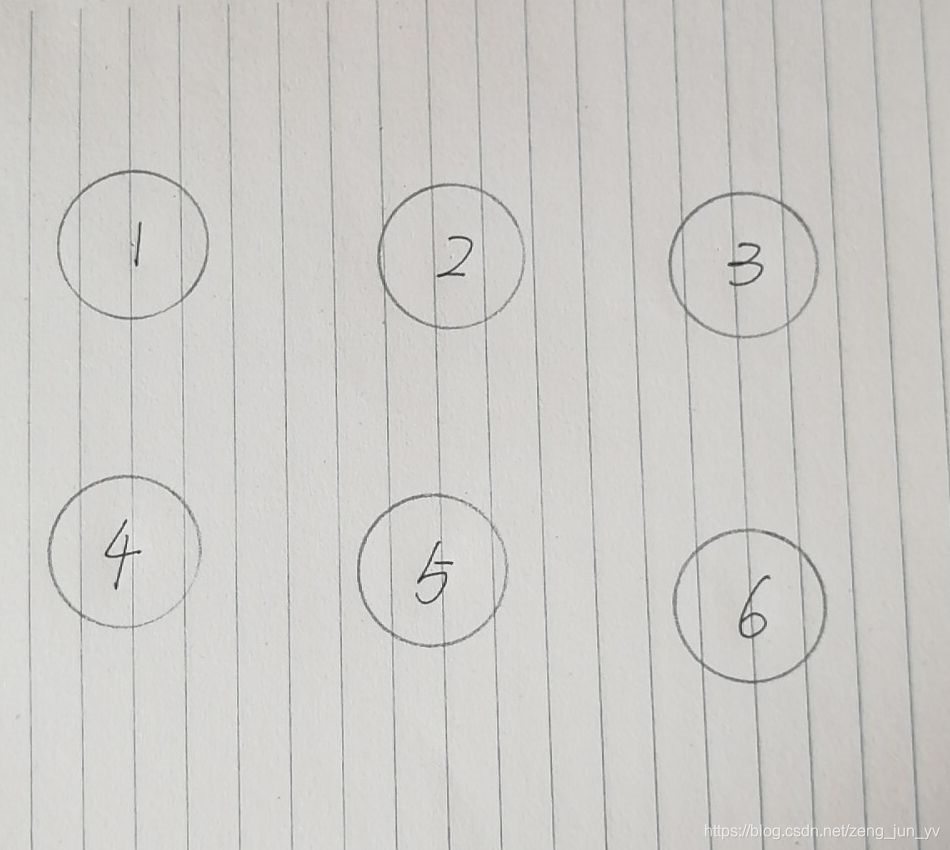
2.现在我来给他们一些联系，然后可以根据联系进行集合的一个合并，随机得到一个树状结构

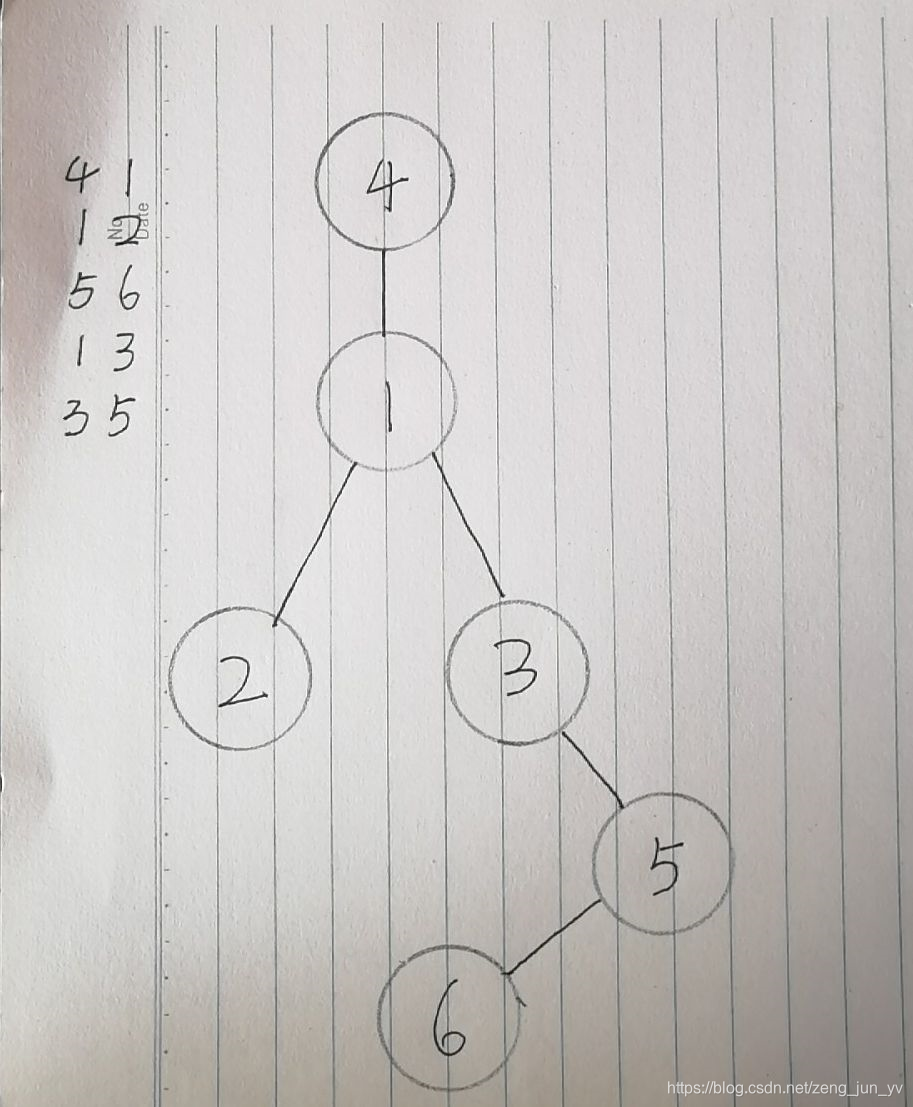
只要是能通过关系串联起来的，不管是直接联系还是间接联系，元素通过两两之间的关系串联起来，把他们都归到同一个集合。那么如何判断两个元素是否属于一个集合呢？

我们可以在每个集合内确定一个祖宗节点，你们可以认为是一个特殊点，作为参照。这样，两个集合只要互相确认自己的祖宗节点是不是同一个，就可以确定关系了。

但是还有问题啊，目前我们只知道直接的联系，那么我们就需要对集合进行操作，形成树状结构，祖宗节点就是根节点，下面分别是二级、三级…。每个人只要记住自己的上级是谁就行了。那么判断是否属于同一个集合，只要一层层向上查找，直到最高层，就可以在短时间内确定了。由于我们关心的只是两个元素是否在同一个集合的，至于他们是如何通过关系相关联的，以及每个圈子内部的结构是怎样的，甚至祖宗节点是谁，都不重要了，就可以随机确定上下级关系
3.我们最终经过处理，实现的是如图所示

接下来是对代码实现的一个讲解

一般来说，一个并查集代码实现对应三个重要步骤：初始化+查找根结点函数+合并集合函数

【初始化】

这个集合的类别pre（其实就是一个指针，用来指示这个集合属于那一类，合并过后的集合，他们的pre指向的最终值一定是相同的）
初始化的时候，每一个集合的pre都是这个集合自己的标号。没有跟它同类的集合，那么这个集合的源头只能是自己了。

int pre[max];   //集合index的类别，或者用parent表示
//初始化集合
void init()
{    for(int i=1;i<=n;i++)pre[i]=i;   //一个集合的pre都是这个集合自己的标号。没有跟它同类的集合，那么这个集合的源头只能是自己了。 
}

【查找函数】

就是找到pre指针的源头，可以把函数命名为find，如果集合的pre等于集合的编号（即还没有被合并或者没有同类），那么自然返回自身编号。 如果不同（即经过合并操作后指针指向了源头（合并后选出的rank高的集合））那么就可以调用递归函数，如下面的代码：

//查找集合i（一个元素是一个集合）的源头（递归实现）
int Find(int i)
{//如果集合i的父亲是自己，说明自己就是源头，返回自己的标号if(pre[i]==i)return pre[i];//否则查找集合i的父亲的源头return  Find(pre[i]);       
}

递归，这个已经讲过很多次，这里就不再多讲，大家可以结合浏览器的后退功能，如果你想追溯源头，你就一直回溯，就能找到。

【合并】

将两个元素所在的集合合并为一个集合。
通常来说，合并之前，应先判断两个元素是否属于同一集合，这可用上面的"查找"操作实现。那么我们如何合并两个不相交集合（Union(x,y)）
合并操作很简单：先设置一个数组pre[x]，表示x的“父亲”的编号。那么，合并两个不相交集合的方法就是，找到其中一个集合祖宗节点，将另外一个集合的祖宗节点的父亲指向它。

int gets(int a,int b){int x=Find(a);int y=Find(b);if(x!=y)pre[y]=x;}

算法描述总结

关键特征：
①用集合中的某个元素来代表这个集合~~，该元素称为集合的代表元；~~
②构成了一个以代表元素为根的树形结构；
③对于每一个元素 pre[x]指向x在树形结构上的父亲节点。如果x是根节点，则令pre[x] = x；
④对于查找操作，假设需要确定x所在的的集合，也就是确定集合的代表元。可以沿着pre[x]不断在树形结构中向上移动，直到到达根节点。
判断两个元素是否属于同一集合，只需要看他们的代表元是否相同即可。
用途：
1、维护无向图的连通性。支持判断两个点是否在同一连通块内，和判断增加一条边是否会产生环。
2、用在求解最小生成树的Kruskal算法里。
如果还有哪里我讲的不清楚，或是有疑问，欢迎私聊我，我会为你们解答。

贴上其他博客讲解并查集的1 2 3 4