目录
- 符号
- 整除/同余理论常见符号
- 数论函数常见符号
- 其他常见符号
- 位运算
- 与、或、异或
- 取反
- 左移和右移
- 复合赋值位运算符
- 关于优先级
- 位运算的应用
- 有关 2 的幂的应用
- 取绝对值
- 取两个数的最大/最小值
- 操作一个数的二进制位
- 模拟集合操作
- 快速幂
- 模意义下大整数乘法
- 快速乘
- 高精度快速幂
- 欧拉降幂
- 求解因数和
- 节省时间的素数筛
- 欧拉筛
- 卢卡斯定理
- 逆元
- 求逆元的三种方法
- (1)扩展欧几里得法
- (2)费马小定理
- (3)欧拉函数法
- (4)不互质求逆元
- 欧拉函数法(求阶乘逆元)
- 进位制
- 矩阵快速幂
- (1)矩阵推导
- 莫比乌斯反演
- 组合数学
- 斐波那契数列
- 博弈论
- 尼姆游戏 Nim Game
- 巴什博弈 Bash Game
- 威佐夫博弈 Wythoff Game
- 斐波那契博弈(一)
- 斐波那契博弈(二)
- SG
- Anti-Nim游戏
- 尼姆博弈
- (1)第一个类型
- (2)第二个类型
- (3)第三个类型
- (4)第四种类型
- 第五个类型:尼姆博弈求可行方案数目
- Anti-SG游戏
- Multi - SG游戏
- 打表
- AC:
- 数学问题的解题技巧:
- 弹性碰撞
- 折半枚举
- 拓展欧几里得
- 唯一分解定理
- 开关问题:
- 尺取法
- 约瑟夫环
- 阶乘
- 求阶乘的的位数
- 求阶乘最后非零数
- 数论相关公式
- 欧拉定理
- 费马定理
- Polya定理
- 欧拉函数 φ(n)
- 2n2^{n}2n 位数
- 默慈金数 HVD 问题
符号
整除/同余理论常见符号
整除符号:x∣yx\mid yx∣y,表示xxx 整除yyy ,即 xxx是 yyy 的因数。
取模符号:xxx modmodmod yyy,表示xxx 除以yyy 得到的余数。
互质符号:x⊥yx\perp yx⊥y,表示 xxx,yyy 互质。
最大公约数:gcd(x,y)gcd(x,y)gcd(x,y),在无混淆意义的时侯可以写作(x,y)(x,y)(x,y) 。
最小公倍数:lcm(x,y)lcm(x,y)lcm(x,y),在无混淆意义的时侯可以写作[x,y]\left [ x,y \right ][x,y] 。
数论函数常见符号
求和符号: ∑\sum∑符号,表示满足特定条件的数的和。举几个例子:
-
∑i=1n\sum^{n}_{i=1}∑i=1n 表示1+2+...+n1+2+...+n1+2+...+n 的和。其中 iii 是一个变量,在求和符号的意义下 iii通常是 正整数或者非负整数(除非特殊说明)。这个式子的含义可以理解为, 从 1 循环到nnn ,所有 iii的和。这个式子用代码的形式很容易表达。当然,学过简单的组合数学的同学都知道∑i=1n=n(n+1)2\sum^{n}_{i=1}=\frac{n(n+1)}{2}∑i=1n=2n(n+1) 。
-
∑S⊆T∣S∣\sum_{S\subseteq T}|S|∑S⊆T∣S∣ 表示所有被 TTT包含的集合的大小的和。
-
∑p≤n,p⊥n\sum_{p\leq n,p\perp n}∑p≤n,p⊥n 1表示的是nnn 以内有多少个与 nnn互质的数,即φ(n)\varphi(n)φ(n) , φ\varphiφ是欧拉函数。
求积符号: ∏\prod∏符号,表示满足特定条件的数的积。举几个例子: -
∏i=1n\prod^{n}_{i=1}∏i=1n 表示nnn 的阶乘,即 n!n!n!。
-
∏i=1nai\prod^{n}_{i=1}a_{i}∏i=1nai 表示a1∗a2∗a3∗...∗ana_{1}*a_{2}*a_{3}*...*a_{n}a1∗a2∗a3∗...∗an。
-
∏x∣dx\prod_{x|d}x∏x∣dx 表示 ddd的所有因数的乘积。
在行间公式中,求和符号与求积符号的上下条件会放到符号的上面和下面,这一点要注意。
其他常见符号
阶乘符号 !!!, n!n!n!表示1∗2∗3∗...∗n1*2*3*...*n1∗2∗3∗...∗n 。特别地,0!=10!=10!=1。
向下取整符号⌊x⌋\left \lfloor x \right \rfloor⌊x⌋:,表示小于等于 xxx 的最大的整数。常用于分数,比如分数的向下取整⌊xy⌋\left \lfloor \frac{x}{y} \right \rfloor⌊yx⌋ 。
向上取整符号⌈x⌉\left \lceil x \right \rceil⌈x⌉:,与向下取整符号相对,表示大于等于 xxx的最小的整数。
位运算
位运算就是基于整数的二进制表示进行的运算。由于计算机内部就是以二进制来存储数据,位运算是相当快的。
基本的位运算共6 种,分别为按位与、按位或、按位异或、按位取反、左移和右移。
为了方便叙述,下文中省略“按位”。
与、或、异或
这三者都是两数间的运算,因此在这里一起讲解。
它们都是将两个整数作为二进制数,对二进制表示中的每一位逐一运算。
| 运算 | 运算符 | 数学符号表示 | 解释 |
|---|---|---|---|
| 与 | δ\deltaδ | & 、and | 只有两个对应位都为 1 时才为 1 |
| 或 | ∣\mid∣ | ∣\mid∣、or | 只要两个对应位中有一个1 时就为1 |
| 异或 | ^ | ⨁、xor | 只有两个对应位不同时才为 1 |
注意区分逻辑与(对应的数学符号为 ∧)和按位与、逻辑或(∨)和按位或的区别。
异或运算的逆运算是它本身,也就是说两次异或同一个数最后结果不变,即 a⨁b⨁b=aa⨁b⨁b=aa⨁b⨁b=a 。
举例:
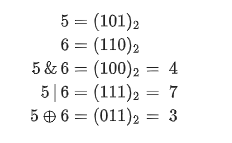
取反
取反是对一个数 num 进行的位运算,即单目运算。
取反暂无默认的数学符号表示,其对应的运算符为 ~。它的作用是把 num 的二进制补码中的 0和 1 全部取反( 0变为1 ,1 变为 0)。有符号整数的符号位在 ~ 运算中同样会取反。
补码:在二进制表示下,正数和0 的补码为其本身,负数的补码是将其对应正数按位取反后加一。
举例(有符号整数):

左移和右移
num << i 表示将 num 的二进制表示向左移动 i位所得的值。
num >> i 表示将num 的二进制表示向右移动i 位所得的值。
举例:

移位运算中如果出现如下情况,则其行为未定义:
- 右操作数(即移位数)为负值;
- 右操作数大于等于左操作数的位数;
例如,对于 int 类型的变量 a , a<<-1 和 a<<32 都是未定义的。
对于左移操作,需要确保移位后的结果能被原数的类型容纳,否则行为也是未定义的。对一个负数执行左移操作也未定义。
对于右移操作,右侧多余的位将会被舍弃,而左侧较为复杂:对于无符号数,会在左侧补 ;而对于有符号数,则会用最高位的数(其实就是符号位,非负数为 ,负数为 )补齐。
复合赋值位运算符
和 += , -= 等运算符类似,位运算也有复合赋值运算符: &= , |= , ^= , <<= , >>= 。(取反是单目运算,所以没有。)
关于优先级
位运算的优先级低于算术运算符(除了取反),而按位与、按位或及异或低于比较运算符,所以使用时需多加注意,在必要时添加括号。
位运算的应用
位运算一般有三种作用:
- 高效地进行某些运算,代替其它低效的方式。
- 表示集合。(常用于 状压 DP 。)
- 题目本来就要求进行位运算。
需要注意的是,用位运算代替其它运算方式(即第一种应用)在很多时候并不能带来太大的优化,反而会使代码变得复杂,使用时需要斟酌。(但像“乘 2 的非负整数次幂”和“除以 2 的非负整数次幂”就最好使用位运算,因为此时使用位运算可以优化复杂度。)
有关 2 的幂的应用
由于位运算针对的是变量的二进制位,因此可以推广出许多与 2 的整数次幂有关的应用。
- 将一个数乘(除) 2 的非负整数次幂:
int mulPowerOfTwo(int n, int m) { // 计算 n*(2^m)return n << m;
}
int divPowerOfTwo(int n, int m) { // 计算 n/(2^m)return n >> m;
}
Warning
我们平常写的除法是向 取整,而这里的右移是向下取整(注意这里的区别),即当数大于等于 时两种方法等价,当数小于 时会有区别,如: -1 / 2 的值为 ,而 -1 >> 1 的值为 。
判断一个数是不是2 的非负整数次幂:
bool isPowerOfTwo(int n) {return n > 0 && (n & (n - 1)) == 0;
}
对2 的非负整数次幂取模:
int modPowerOfTwo(int x, int mod) { return x & (mod - 1);
}
取绝对值
在某些机器上,效率比 n > 0 ? n : -n 高。
int Abs(int n) {return (n ^ (n >> 31)) - (n >> 31);/* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1)需要计算 n 和 -1 的补码,然后进行异或运算,结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */
}
取两个数的最大/最小值
在某些机器上,效率比 a > b ? a : b 高。
/ 如果 a>=b,(a-b)>>31 为 0,否则为 -1
int max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }
int min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); }
判断两非零数符号是否相同
bool isSameSign(int x, int y) { // 有 0 的情况例外return (x ^ y) >= 0;
}
操作一个数的二进制位
获取一个数二进制的某一位:
// 获取 a 的第 b 位,最低位编号为 0
int getBit(int a, int b) { return (a >> b) & 1;
}
将一个数二进制的某一位设置为 0:
// 将 a 的第 b 位设置为 0 ,最低位编号为 0
int unsetBit(int a, int b) { return a & ~(1 << b);
}
将一个数二进制的某一位设置为1 :
// 将 a 的第 b 位设置为 1 ,最低位编号为 0
int setBit(int a, int b) { return a | (1 << b);
}
将一个数二进制的某一位取反:
// 将 a 的第 b 位取反 ,最低位编号为 0
int flapBit(int a, int b) { return a ^ (1 << b);
}
这些操作相当于将一个 位32整型变量当作一个长度为32 的布尔数组。
模拟集合操作
一个数的二进制表示可以看作是一个集合( 表示不在集合中, 表W示在集合中)。比如集合 {1, 3, 4, 8} ,可以表示成(100011010)2(100011010)_{2}(100011010)2 。而对应的位运算也就可以看作是对集合进行的操作。
| 操作 | 集合表示 | 位运算语句 |
|---|---|---|
| 交集 | a∩ba∩ba∩b | a & b |
| 并集 | a∪ba∪ba∪b | a∣ba∣ba∣b |
| 补集 | aˉ\bar{a}aˉ | ~a (全集为二进制都是 1) |
| 差集 | a\b | a & (~b) |
| 对称差 | a△ba△ba△b | a ^ b |
子集遍历:
// 遍历 u 的非空子集
for (int s = u; s; s = (s - 1) & u) {// s 是 u 的一个非空子集
}
快速幂
(1)Pseudoprime numbers POJ - 3641(快速幂+判素数)
(2)Colossal Fibonacci Numbers! UVA - 11582(斐波那契求模)+快速幂+周期规律
模意义下大整数乘法
举例:计算a∗ba*ba∗b mod m,a,b<=m<=1019m,a,b<=m<=10^{19}m,a,b<=m<=1019 。
与二进制取幂的思想一样,这次我们将其中的一个乘数表示为若干个 2 的整数次幂的和的形式。因为在对一个数做乘 2 并取模的运算的时侯,我们可以转化为加减操作防止溢出。这样仍可以在 O(log2m)O(log_{2}m)O(log2m) 的时内解决问题。递归方法如下:

快速乘
但是 O(log2m)O(log_{2}m)O(log2m) 的“龟速乘”还是太慢了,这在很多对常数要求比较高的算法比如 Miller_Rabin 和 Pollard-Rho 中,就显得不够用了。所以我们要介绍一种可以处理模数在 long long 范围内、不需要使用黑科技 __int128 的、复杂度为O()1 的“快速乘”。
我们发现:
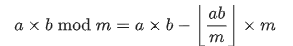
我们巧妙运用 unsigned long long 的自然溢出:

于是在算出⌊abm⌋\left \lfloor \frac{ab}{m} \right \rfloor⌊mab⌋ 后,两边的乘法和中间的减法部分都可以使用 unsigned long long 直接计算,现在我们只需要解决如何计算⌊abm⌋\left \lfloor \frac{ab}{m} \right \rfloor⌊mab⌋ 。
我们考虑先使用 long double 算出 ap\frac{a}{p}pa 再乘上b 。
既然使用了 long double,就无疑会有进度误差。极端情况就是第一个有效数字在小数点后一位。因为 sizeof(long double)=16,即 long double 的进度是 64 位有效数字。所以 ap\frac{a}{p}pa 从第 65 位开始出错,误差范围为(−2−64,264-2^{-64},2^{64}−2−64,264) 。乘上b 这个 64位整数,误差范围为 (-0.5,0.5),再加上0.5 误差范围为(0,1) ,取整后误差范围位 {0,1}。于是乘上 -m 后,误差范围变成 (0,-m),我们需要判断这两种情况。
因为 m在 long long 范围内,所以如果计算结果 r 在 [0,m) 时,直接返回r ,否则返回 r+m,当然你也可以直接返回 (r+m)mod m。
代码实现如下:
long long binmul(long long a, long long b, long long m) {unsigned long long c =(unsigned long long)a * b - (unsigned)((long double)a / m * b + 0.5L) * m;if (c < m) return c;return c + m;
}
高精度快速幂
题目大意:从文件中输入P(1000<P<3100000),计算2p−12^{p}-12p−1 的最后 100 位数字(用十进制高精度数表示),不足 100 位时高位补 0。
#include <bits/stdc++.h>
using namespace std;
int a[505], b[505], t[505], i, j;
int mult(int x[], int y[]) // 高精度乘法
{memset(t, 0, sizeof(t));for (i = 1; i <= x[0]; i++) {for (j = 1; j <= y[0]; j++) {if (i + j - 1 > 100) continue;t[i + j - 1] += x[i] * y[j];t[i + j] += t[i + j - 1] / 10;t[i + j - 1] %= 10;t[0] = i + j;}}memcpy(b, t, sizeof(b));
}
void ksm(int p) // 快速幂
{if (p == 1) {memcpy(b, a, sizeof(b));return;}ksm(p / 2);mult(b, b);if (p % 2 == 1) mult(b, a);
}
int main() {int p;scanf("%d", &p);a[0] = 1;a[1] = 2;b[0] = 1;b[1] = 1;ksm(p);for (i = 100; i >= 1; i--) {if (i == 1) {printf("%d\n", b[i] - 1);} elseprintf("%d", b[i]);}
}
欧拉降幂
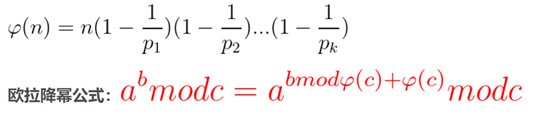
求解因数和
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int N=5e5+10;int ans[N];
void init(){for(int i=1; i<N; ++i) ans[i]=1;for(int i=2; i<N; ++i){for(int j=1; j<=N/i; ++j){ans[i*j]+=i;}}
}int main()
{init();int q; scanf("%d",&q);while(q--){int n; scanf("%d",&n);printf("%d\n",ans[n]);}return 0;
}
节省时间的素数筛
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<queue>
#include<bitset>
#include<iostream>
#include<vector>
#include<map>
#include<stdlib.h>
#include<string>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define PI acos(-1.0)
#define eps 1e-8
const int N=100000005;
const int M=5800000;
const ll mod=1ll<<32;
bitset<N> bt;
int k,t,n;
unsigned int tag[M];//不能用long long要不然会爆内存
unsigned int sum[M];
void su()
{k=1;for(int i=2;i<N;i++){if(bt[i]==0)tag[k++]=i;for(int j=1;j<k&&i*tag[j]<N;j++){bt[i*tag[j]]=1;if(i%tag[j]==0)break;}}sum[0]=1;for(int i=1;i<k;i++)//前缀和,要不然会超时sum[i]=tag[i]*sum[i-1];
}
ll Pow(int a,int b)//快速幂
{ll ans=1;while(b){if(b%2==1)ans=ans*a%mod;a=a*a%mod;b=b/2;}return ans;
}
int main()
{su();int kk=1;scanf("%d",&t);while(t--){scanf("%d",&n);int h=upper_bound(tag+1,tag+k,n)-tag-1;//查找大于n的第一个素数的位置ll S=sum[h]%mod;for(int i=1;i<k&&tag[i]*tag[i]<=n;i++){int p=n,w=0;while(p/tag[i])p=p/tag[i],w++;//找个此素数的最大次方值S=S*Pow(tag[i],--w)%mod;}printf("Case %d: %lld\n",kk++,S);}
}
欧拉筛
void Phi()
{phi[1]=1;for (int i=2; i<4000005; i++)if (!phi[i])for (int j=i; j<4000005; j+=i){if (!phi[j])phi[j]=j;phi[j]=phi[j]/i*(i-1);}
}
调和级数

公式:f(n)=ln(n)+C+1/(2*n), 公式中C≈0.57721566490153286060651209;但是使用的时候n不能过小, 10000以上的数就可以用这个公式,剩下的就是打表,10000以内的数打表应该非常容易。
卢卡斯定理
求CmnmodC_{m}^{n}modCmnmod ppp 的值;
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mulit(ll a,ll b,ll m)
{ll ans=0;while(b){if(b&1)ans=(ans+a)%m;a=(a<<1)%m;b>>=1;}return ans;
}
ll quick_mod(ll a,ll b,ll m)
{ll ans=1;while(b){if(b&1)ans=mulit(ans,a,m);a=mulit(a,a,m);b>>=1;}return ans;
}
ll comp(ll a,ll b,ll m)
{if(a<b)return 0;if(a==b)return 1;if(b>a-b)b=a-b;ll ans=1,ca=1,cb=1;for(int i=0; i<b; i++){ca=ca*(a-i)%m;cb=cb*(b-i)%m;}ans=ca*quick_mod(cb,m-2,m)%m;return ans;
}
ll lucas(ll a,ll b,ll m)
{ll ans=1;while(a&&b){ans=(ans*comp(a%m,b%m,m))%m;a/=m,b/=m;}return ans;
}
int main()
{ll n,m,p;int t;cin>>t;while(t--){cin>>n>>m>>p;cout<<lucas(a,b,m)<<endl;}return 0;
}
逆元
(1)Divide and Sum CodeForces - 1445D(排列组合+逆元)
(2)A/B HDU - 1576 (逆元或拓展欧几里得或数学公式)多解法求大数结果
求逆元的三种方法
(1)扩展欧几里得法
限制条件:a和mod互质才能用
void exgcd(LL a,LL b,LL &d,LL &x,LL &y)//扩展欧几里得算法
{if(b==0)d=a,x=1,y=0;else {exgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
LL getInv(int a,int mod)//求a在mod下的逆元,不存在逆元返回-1
{LL x,y,d;exgcd(a,mod,d,x,y);//d表示最大公因数return d==1?(x%mod+mod)%mod:-1;
}
(2)费马小定理
限制条件:mod必须为质数
void exgcd(LL a,LL b,LL &d,LL &x,LL &y)//扩展欧几里得算法
{if(b==0)d=a,x=1,y=0;else {exgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
LL getInv(int a,int mod)//求a在mod下的逆元,不存在逆元返回-1
{LL x,y,d;exgcd(a,mod,d,x,y);//d表示最大公因数return d==1?(x%mod+mod)%mod:-1;
}
(3)欧拉函数法
a 和 m 互质,快速幂取模
long long powM(long long a, long long b, long long m)
{long long tmp = 1;if (b == 0) {return 1;}if (b == 1){return a % m;}tmp = powM(a, b >> 1, m);tmp = tmp * tmp % m;if (b & 1){tmp = tmp * a % m;}return tmp;
}long long inv(long long a, long long m)
{return powM(a, m - 2, m);
}
(4)不互质求逆元
题意:输入n,k ,令m=(2008n2008^{n}2008n的因子和)mod k,输出 (2008m2008^{m}2008m)mod k。
思路:本题中,先求出m,即约数和,2008可以被分解为 23∗2512^{3}*25123∗251 ,250作为分母被除然后对k取模,但是K不一定是素数,即不一定与250互素,所以不能求逆元。我们应用公式x/d%m = x%(dm)/d 来求:所以在使用快速幂时 应对 dm来取模,而不是m。
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef long long ll;
ll pow(ll x,ll y,ll mod)
{x=x%mod;ll sum=1;while(y>0){if(y%2!=0)sum=(sum*x)%mod;x=x*x%mod;y=y/2;}return sum%mod;
}
int main()
{int n,m;while(~scanf("%d%d",&n,&m)&&(n||m)){ll a=(pow(2,3*n+1,m*250)-1)%(250*m);ll b=(pow(251,n+1,m*250)-1)%(250*m);ll k=a*b%(250*m)/250;printf("%lld\n",pow(2008,k,m));}
}
欧拉函数法(求阶乘逆元)
typedef long long ll;const ll MOD = 1e9 + 7; // 必须为质数才管用
const ll MAXN = 1e5 + 3;ll fac[MAXN]; // 阶乘
ll inv[MAXN]; // 阶乘的逆元ll QPow(ll x, ll n)
{ll ret = 1;ll tmp = x % MOD;while (n){if (n & 1){ret = (ret * tmp) % MOD;}tmp = tmp * tmp % MOD;n >>= 1;}return ret;
}void init()
{fac[0] = 1;for (int i = 1; i < MAXN; i++){fac[i] = fac[i - 1] * i % MOD;}inv[MAXN - 1] = QPow(fac[MAXN - 1], MOD - 2);for (int i = MAXN - 2; i >= 0; i--){inv[i] = inv[i + 1] * (i + 1) % MOD;}
}
进位制
八进制数以 oxx(其中 o 为八进制的前缀,xx 代表八进制数)的形式来表示。
十六进制数以 0xdbf(其中 0x 为十六进制数的前缀)的形式来表示。
十进制转二进制/八进制/十六进制¶
这里以二进制为例来演示,其他进制的原理与其类似。
整数部分,把十进制数不断执行除 2 操作,直至商数为 0。读余数从下读到上,即是二进制的整数部分数字。小数部分,则用其乘 2,取其整数部分的结果,再用计算后的小数部分依此重复计算,算到小数部分全为 0 为止,之后从上到下,读所有计算后整数部分的数字,即为二进制的小数部分数字。
将33.25转化为二进制数
整数部分:
33/2=16 ......1
16/2=8 ......0
8/2=4 ......0
4/2=2 ......0
2/2=1 ......0
1/2=0 ......1
小数部分:
0.25*2=0.5 0
0.5*2=1 1

矩阵快速幂
(1)矩阵推导
【1】数列f[n]=f[n−1]+f[n−2],f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n−2],f[n−1],s[n−2]】∗A=【f[n−1],f[n],s[n−1]】=【f[n−1],f[n−1]+f[n−2],s[n−2]+f[n−1]】f[n]=f[n-1]+f[n-2],f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n-2],f[n-1],s[n-2]】* A = 【f[n-1],f[n],s[n-1]】=【f[n-1],f[n-1]+f[n-2],s[n-2]+f[n-1]】f[n]=f[n−1]+f[n−2],f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n−2],f[n−1],s[n−2]】∗A=【f[n−1],f[n],s[n−1]】=【f[n−1],f[n−1]+f[n−2],s[n−2]+f[n−1]】
得到这个3×3的矩阵A是:
0 1 0
1 1 1
0 0 1
【2】数列f[n]=f[n−1]+f[n−2]+n+1,f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n−2],f[n−1],s[n−2],n,1】∗A=【f[n−1],f[n],s[n−1],n+1,1】=【f[n−1],f[n−1]+f[n−2]+n+1,s[n−2]+f[n−1],n+1,1】f[n]=f[n-1]+f[n-2]+n+1,f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n-2],f[n-1],s[n-2],n,1】* A =【f[n-1],f[n],s[n-1],n+1,1】=【f[n-1], f[n-1]+f[n-2]+n+1,s[n-2]+f[n-1],n+1,1】f[n]=f[n−1]+f[n−2]+n+1,f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).即:【f[n−2],f[n−1],s[n−2],n,1】∗A=【f[n−1],f[n],s[n−1],n+1,1】=【f[n−1],f[n−1]+f[n−2]+n+1,s[n−2]+f[n−1],n+1,1】
构造出A为:
0 1 0 0 0
1 1 1 0 0
0 0 1 0 0
0 1 0 1 0
0 1 0 1 1
故:【f(1),f(2),s(1),3,1】∗A(n−1)=【f(n),f(n+1),s(n),n+2,1】一般地,如果有f[n]=p∗f[n−1]+q∗f[n−2]+r∗n+s【f(1),f(2),s(1),3,1】* A^(n-1) = 【f(n),f(n+1),s(n),n+2,1】 一般地,如果有f[n]=p*f[n-1]+q*f[n-2]+r*n+s【f(1),f(2),s(1),3,1】∗A(n−1)=【f(n),f(n+1),s(n),n+2,1】一般地,如果有f[n]=p∗f[n−1]+q∗f[n−2]+r∗n+s
可以构造矩阵A为:
0 q 0 0 0
1 p 1 0 0
0 0 1 0 0
0 r 0 1 0
0 s 0 1 1
例如:A(0)=1,A(1)=1,A(N)=X∗A(N−1)+Y∗A(N−2)(N>=2);给定三个值N,X,Y求S(N):S(N)=A(0)2+A(1)2+……+A(n)2。考虑1∗4的矩阵【s[n−2],a[n−1]2,a[n−2]2,a[n−1]∗a[n−2]】我们需要找到一个4×4的矩阵A,使得它乘以A得到1×4的矩阵【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】即:【s[n−2],a[n−1]2,a[n−2]2,a[n−1]∗a[n−2]】∗A=【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】=【s[n−2]+a[n−1]2,x2∗a[n−1]2+y2∗a[n−2]2+2∗x∗y∗a[n−1]∗a[n−2],a[n−1]2,x∗a[n−1]2+y∗a[n−2]a[n−1]】A(0) = 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2);给定三个值N,X,Y求S(N):S(N) = A(0)2 +A(1)2+……+A(n)2。 考虑1*4 的矩阵【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】 我们需要找到一个4×4的矩阵A,使得它乘以A得到1×4的矩阵 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】 即:【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】* A = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】= 【s[n-2]+a[n-1]^2 , x^2 * a[n-1]^2 + y^2 * a[n-2]^2 + 2*x*y*a[n-1]*a[n-2] ,a[n-1]^2 , x*a[n-1]^2 + y*a[n-2]a[n-1]】A(0)=1,A(1)=1,A(N)=X∗A(N−1)+Y∗A(N−2)(N>=2);给定三个值N,X,Y求S(N):S(N)=A(0)2+A(1)2+……+A(n)2。考虑1∗4的矩阵【s[n−2],a[n−1]2,a[n−2]2,a[n−1]∗a[n−2]】我们需要找到一个4×4的矩阵A,使得它乘以A得到1×4的矩阵【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】即:【s[n−2],a[n−1]2,a[n−2]2,a[n−1]∗a[n−2]】∗A=【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】=【s[n−2]+a[n−1]2,x2∗a[n−1]2+y2∗a[n−2]2+2∗x∗y∗a[n−1]∗a[n−2],a[n−1]2,x∗a[n−1]2+y∗a[n−2]a[n−1]】
可以构造矩阵A为:
1 0 0 0
1 x^2 1 x
0 y^2 0 0
0 2xy 0 y
故:【S[0],a[1]2,a[0]2,a[1]∗a[0]∗A(n−1)=【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】所以:【S[0],a[1]2,a[0]2,a[1]∗a[0]∗A(n)=【s[n],a[n+1]2,a[n]2,a[n+1]∗a[n]】若A=(B∗C)则AT=(B∗C)T=CT∗BT【S[0],a[1]^{2},a[0]^2,a[1]*a[0] * A^(n-1) = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】 所以:【S[0],a[1]^2,a[0]^2,a[1]*a[0] * A^(n) = 【s[n],a[n+1]^2,a[n]^2,a[n+1]*a[n]】 若A = (B * C ) 则AT = ( B * C )T = CT * BT【S[0],a[1]2,a[0]2,a[1]∗a[0]∗A(n−1)=【s[n−1],a[n]2,a[n−1]2,a[n]∗a[n−1]】所以:【S[0],a[1]2,a[0]2,a[1]∗a[0]∗A(n)=【s[n],a[n+1]2,a[n]2,a[n+1]∗a[n]】若A=(B∗C)则AT=(B∗C)T=CT∗BT
故
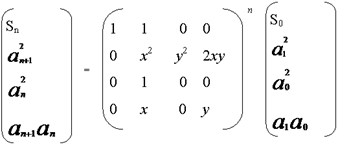
(2)矩阵模板
求斐波那契的前n项和对mod求余
打表可推导出s[n]=s[n-1]+s[n-2]+1;
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4;
ll base[N][N];
ll tmp[N][N];
ll n,mod;
void Init()//初始化构造的矩阵
{base[1][1]=0;base[1][2]=1;base[1][3]=0;base[2][1]=1;base[2][2]=1;base[2][3]=0;base[3][1]=0;base[3][2]=1;base[3][3]=1;
}
void mult(ll x[N][N],ll y[N][N])//矩阵相乘
{ll tmp[N][N];for(int i=1;i<N;i++)for(int j=1;j<N;j++){tmp[i][j]=0;for(int k=1;k<N;k++)tmp[i][j]=(tmp[i][j]+x[i][k]*y[k][j])%mod;}memcpy(x,tmp,sizeof(tmp));//复制函数
}
ll fpow(ll b)//矩阵快速幂
{ll ans[N][N];memcpy(ans,base,sizeof(base));while(b){if(b&1)mult(ans,base);mult(base,base);b/=2;}return (1*ans[1][2]+2*ans[2][2]+1*ans[3][2])%mod;
}
int main()
{Init();cin>>n>>mod;if(n==1)printf("1\n");else if(n==2)printf("%lld\n",n%mod);else printf("%lld\n",fpow(n-3));
}
莫比乌斯反演
莫比乌斯反演是数论中的重要内容。对于一些函数f(n)f(n)f(n) ,如果很难直接求出它的值,而容易求出其倍数和或约数和g(n)g(n)g(n),那么可以通过莫比乌斯反演简化运算,求得 f(n)f(n)f(n)的值。
莫比乌斯反演/容斥 +2020ICPC 江西省大学生程序设计竞赛 A Simple Math Problem
组合数学
(1)Divide and Sum CodeForces - 1445D(排列组合+逆元)
(2)全排列
(3)I - Interesting Permutation Gym - 102394I(排列组合)
斐波那契数列
博弈论
尼姆游戏 Nim Game
题目大意:给定 N NN 堆物品,第i堆物品有Ai个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人都采取最优策略,问先手是否必胜。
解题思路:必败状态:a1 ^ a2^ …^an=0 必胜状态:a1 ^ a2 ^ …^an=k (k!=0) 先手取走若干石子后,就转必胜状态为必败状态
若a1 ^ a2 ^ … ^ an!=0,一定存在某个合法的移动:将 ai 改变成ai’ 后满足a1 ^ a2 ^ … ^ ai ‘^ … ^ an=0
巴什博弈 Bash Game
题目大意:本游戏是一个二人游戏;有一堆石子 一共有n个;两人轮流进行;每走一步可以取走1…m个石子;最先取光石子的一方为胜;
分析:若n%(m+1)==0,则一定后手赢,因为不管先手拿多少个x(小于等于m,大于等于1),后手只要拿(m+1)-x 就好了…
变形:条件不变,改为最后取光的人输。
结论:如果条件是最后取光者失败,那么当先手面临的局势是(n-1)%(m+1)==0时,先手必败。
威佐夫博弈 Wythoff Game
题目大意:有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。
分析:两堆石子为x和y(若x<y) 先手必败状态(奇异局势):当且仅当(y−x)∗(sqrt(5)+1)/2==x时;
问题模型:有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
int main()
{int a,b;while(~scanf("%d%d",&a,&b)){if(a>b)swap(a,b);int ans=floor((b-a)*(sqrt(5)+1)/2); //判断是否是奇异局势if(a==ans)printf("second win\n");elseprintf("first win\n");}return 0;
}
斐波那契博弈(一)
题目大意:这是一个二人游戏;一共有3堆石子,数量分别是m, n, p个;
两人轮流走;每走一步可以选择任意一堆石子,然后取走f个;f只能是菲波那契数列中的元素(即每次只能取1,2,3,5,8…等数量);最先取光所有石子的人为胜者;
分析:SG(x)=mex(SG(所有通过x能达到的”局势“)),那么对于n堆石子的取石子游戏,
若SG(1)SG(2)……^SG(n)==0,则先手必败,否则先手必胜。
这一题的各个状态的SG值是:因为每次可以取走斐波那契数列里的数的石子数,那么对于任意状态i,i-Fibonacci[j]都是可以取到的,故我们需要预处理出Fibonacci数列,然后通过枚举的方法,把i-Fibonacci[j]的SG值全部标记,扫一遍,找到最小的非负整数即为i的SG值
const int N=1e3+10;
int f[20];///斐波那契数列 到16就超过1000了~ m,n,p(1<=m,n,p<=1000)
int sg[N],vis[N];///vis数组记录所有出现过的非负整数
int m,n,p;
int getsg(int x) { ///求sg值f[0]=1,f[1]=1;for(int i=2; i<=20; i++)f[i]=f[i-1]+f[i-2];for(int i=1; i<=1000; i++) {mem(vis,0);for(int j=0; f[j]<=i; j++)vis[sg[i-f[j]]]=1;for(int j=0; j<=1000; j++) { ///求得最小非负整数if(vis[j]==0) {sg[i]=j;break;}}}
}
int main() {getsg(N);int n,m,p;while(~scanf("%d%d%d",&n,&m,&p)) {if(!n&&!m&&!p)break;int ans=sg[n]^sg[m]^sg[p];if(ans)printf("Fibo\n");else printf("Nacci\n");}return 0;
}
斐波那契博弈(二)
题目大意:有一堆个数为n(n>=2)的石子,游戏双方轮流取石子;
先手不能在第一次把所有的石子取完,至少取1颗;
之后每次可以取的石子数至少为1,至多为对手刚取的石子数的2倍。取走最后一个石子的人为赢家,求必败态。
结论:任何正整数可以表示为若干个不连续的Fibonacci数之和,当n为Fibonacci数的时候,必败。f[i]:1,2,3,5,8,13,21,34,55,89…
解决思路:当n为Fibonacci数时,先手必败。即存在先手的必败态当且仅当石头个数为Fibonacci数。
#include<iostream>
using namespace std;
int main()
{long long n,temp,a,b;int mark;while(cin>>n){a=2; b=3; mark=0;while(a<=n){if(a==n||b==n)mark=1;else{temp=a+b; a=b; b=temp; //模拟斐波那契序列}}if(mark)cout<<"Second win"<<endl;else if(!mark)cout<<"First win"<<endl;}return 0;
}
SG
(Sprague−Grundy)定理:所有一般胜利下的公平组合游戏都能转化成尼姆数表达的尼姆堆博弈,一个博弈的尼姆值定义为这个博弈的等价尼姆数;
对于当前游戏 X,它可以拆分成若干个子游戏 x 1 , x 2 , . . . , xn 那么 SG ( X ) = SG(x1) ⊕ SG(x2) ⊕ . . . ⊕ SG (xn)
分析:对于由 n个有向图游戏组成的组合游戏 设它们的起点分别为 s 1 , s 2 , . . . , s n
好多个起点,有好多个博弈图,也就是有好多个;
则当且仅当SG(s1)⊕SG(s2)⊕…⊕SG(sn) =0时,这个游戏为先手必胜 。
Anti-Nim游戏
大意:有 n 堆石子,两个人可以从任意一堆石子中拿任意多个石子(不能不拿),拿走最后一个石子的人失败。问谁会胜利
分析:先手必胜当且仅当:
∀ 所有堆的石子数都为 1且游戏的SG值为 0。
∃ 有些堆的石子数大于 1且游戏的SG值不为 0 。
题目大意:桌子上有n堆石子,小约翰和他的哥哥轮流取石子,每个人取的时候,可以随意选择一堆石子,在这堆石子中取走任意多的石子,但不能一粒石子也不取,我们规定取到最后一粒石子的人算输。
const int N = 2e5 + 7;
int n, m, t, k;
int a[N];
int main() {scanf("%d", &t);while(t -- ) {scanf("%d", &n);int sg = 0;bool flag = 0;for(int i = 1; i <= n; ++ i) {scanf("%d", &a[i]);sg ^= a[i];if(a[i] > 1)flag = 1;}if((flag == 0 && sg == 0) || (flag == 1 && sg != 0)) {puts("John");} else puts("Brother");}return 0;
}
尼姆博弈
尼姆博弈:有任意堆物品,每堆物品的个数是任意的,双方轮流从中取物品,每一次只能从一堆物品中取部分或全部物品,最少取一件,取到最后一件物品的人获胜。
#include <cstdio>
#include <cmath>
#include <iostream>
using namespace std;
int main()
{ int n,ans,temp; while(cin>>n) { temp=0; for(int i=0;i<n;i++) { cin>>ans; temp^=ans; } if(temp==0) cout<<"后手必胜"<<endl; else cout<<"先手必胜"<<endl; } return 0;
}
(1)第一个类型
就是让其判断胜利的人,对n堆石子求异或和,根据当Nim和!= 0时,先手胜利,否则失败就能判断出来。
(2)第二个类型
先取完者判输,统计一下所有数一下大于1的个数,并将所有数字异或一遍,若大于1的个数为0&&异或和为0||大于1的个数大于0&&异或和不为零,则先手胜,否则后手胜。
#include<cstdio>
int main()
{int t,m,n;scanf("%d",&t);while(t--){int ans=0,c=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&m);if(m>1) c++;//统计富裕堆个数ans^=m;}if((!ans && c<2) || (ans && c)) printf("先手胜\n");else printf("后手胜\n");}return 0;
}
(3)第三个类型
限制最多取的个数,例如第i堆石子共有m个,最多取r个,先对m=m%(r+1);然后在进行异或求和。再根据异或和判断输赢。
(4)第四种类型
先手的人想赢,第一步有多少种选择。当先手必输时,很显然是0。如果先手赢,那么先手必须努力创造奇异局势,即让其剩余的石子量异或和为0,上面已经讲了当面对非奇异局势是如何转化成奇异局势。当nim游戏的某个位置:(x1,x2,x3),当且仅当其各部分的nim - sum = 0(即x1(+)x2(+)x3 = 0(也就是各部分的异或为0)) 当前位置为必败点,这对于多个堆的情况同样适用。我们首先求出所有堆异或后的值sum,再用这个值去对每一个堆进行异或,令res = x1(+)sum(sum为所有堆的异或和)。如果res < x1的话,当前玩家就从x1中取走(x1-res)个,使x1乘下res这样必然导致所有的堆的异或值为0,也就是必败点(达到奇异局势),这就是一种方案。遍历每一个堆,进行上面的断判就可以得到总的方案数。
res = x1(+)sum;其实就是除了x1之外的n-1堆异或和,a(+)b(+)c=sum;sum(+)c=a(+)b(+)c(+)c=a(+)b;
第五个类型:尼姆博弈求可行方案数目
#include<iostream>
#include<string.h>
using namespace std;
int main()
{int n,p[111];while(~scanf("%d",&n)&&n){int sum=0;for(int i=0;i<n;i++){scanf("%d",&p[i]);sum^=p[i];}if(!sum)//奇异局势{printf("0\n");continue;}else{int cnt=0;for(int i=0;i<n;i++){if((sum^p[i])<p[i])//此方案下取p[i]-sum^p[i]张形成奇异局势cnt++;}printf("%d\n",cnt);}}return 0;
}
Anti-SG游戏
定义 SJ 定理:对于任意一个 Anti - SG 游戏,如果我们规定:当局面中所有的单一游
戏的SG值为 0 时,游戏结束,
分析:则先手必胜当且仅当:
游戏的 SG 函数值不为 0 且游戏中某个单一游戏的 SG 函数值大于 1。
游戏的SG函数值为 0 且游戏中没有任意一个单一游戏的SG函数值大于 1 。
Multi - SG游戏
定义:游戏规定,在符合拓扑原则的前提下,一个单一游戏的后继可以为 多个单一游戏 。
Multi-SG其他规则与SG游戏相同。
每次操作能将一个当前的单一游戏分为多个单一游戏,也就是将当前这个堆石子分为多堆石子的特殊游戏。
对于一个状态来说,不同的划分方法会产生多个不同的后继,而在一个后继中可能含有多个独立的游戏
一个后继状态的SG值即为后继状态中所有独立游戏的异或和
该状态的 SG 函数值即为后继状态的 SG 函数值中未出现过的最小值
题意:给定n堆石子,两人轮流操作,每次选一堆石子,取任意石子或则将石子分成两个更小的堆(非0),取得最后一个石子的为胜。

打表
const int N = 50007, M = 507;
const int INF = 0x3f3f3f3f;
int sg[N];
bool vis[M + 7];
int main() {sg[0] = 0, sg[1] = 1;for (int i = 2; i < M; ++ i) {memset(vis, 0, sizeof(vis));//操作一,至少取一个for (int j = 1; j <= i; ++ j)vis[sg[i - j]] = 1;//操作二,分成两堆,不为空for (int j = 1; j < i; ++ j)vis[sg[j] ^ sg[i - j]] = 1;int j = 0;while (vis[j]) j ++ ;sg[i] = j;}for (int i = 1; i <= M; ++ i)printf("sg[%d] : %d\n", i, sg[i]);return 0;
}
AC:
int n, a[N], sg[N];
int main() {int t;scanf("%d", &t);while(t -- ) {int ans = 0;scanf("%d", &n);for(int i = 1; i <= n; ++ i)scanf("%d", &a[i]);for(int i = 1; i <= n; ++ i) {if(a[i] % 4 == 0) sg[i] = a[i] - 1;else if(a[i] % 4 == 3) sg[i] = a[i] + 1;else sg[i] = a[i];ans ^= sg[i];}if(ans == 0) puts("Bob");else puts("Alice");}return 0;
}
题目大意:游戏中有 n堆石子,每次行动可以选择:取走某堆的任意数量的石子(不可不取)。将石子拆分成三堆(三堆都不可为空)。最后取走为胜,问先手胜还是后手。
//操作二,分成三堆不为空
for (int j = 1; j <= i; ++ j)for (int k = j; k <= i; ++ k)if ((j + k) < i)vis[sg[k] ^ sg[j] ^ sg[i - j - k]] = 1;
数学问题的解题技巧:
弹性碰撞
Linear world POJ - 2674(弹性碰撞+技巧)
折半枚举
Subset POJ - 3977(折半枚举+二分+二进制枚举)
拓展欧几里得
(1)题目 1886: [蓝桥杯][2017年第八届真题]包子凑数(欧几里得+完全背包)
(2)LightOJ-1220 Mysterious Bacteria (素数打表+欧几里得算法+唯一分解定理)给出x,求x=a^p,最大的指数
(3)A/B HDU - 1576 (逆元或拓展欧几里得或数学公式)多解法求大数结果
基本算法:对于不完全为 0的非负整数 a,b,gcd(a,b)表示a,b的最大公约数,必然存在整数对x,y,使得 gcd(a,b)=ax+by。,具体用处在于:
求解不定方程;
求解模线性方程(线性同余方程);
求解模的逆元;
这里给出一个求解不定方程组解的测试程序:
题目:给出a,b,d,求解x,y;
#include <stdio.h>
int exgcd(int a,int b,int &x,int &y){if(b == 0){x = 1;y = 0;return a;}int d = exgcd(b,a%b,x,y); //d 就是gcd(a,b)int t = x;x = y;y = t-(a/b)*y;return d;
}
bool linear_equation(int a,int b,int c,int &x,int &y){int d = exgcd(a,b,x,y); //d是gcd(a,b)//求出a*x+b*y = gcd(a,b)的一组解printf("%d*x + %d*y = %d(gcd(a,b))的一些解是\n",a,b,d);printf("%d %d\n",x,y); //第一组for(int t = 2; t < 10; t++){ //输出 a*x + b*y = gcd(a,b)的其他一些解int x1 = x + b/d*t;int y1 = y - a/d*t;printf("%d %d\n",x1,y1); //其余组}printf("\n\n"); //第一组if(c%d) return false;int k = c/d; //上述解乘以 c/gcd(a,b)就是 a*x +b*y = c的解x *= k; y *= k; //求得的只是其中一组解return true;
}int main(){int a = 6,b = 15,c = 9; //求解 6*x + 15*y = 9的解int x,y;int d = exgcd(a,b,x,y);if(!linear_equation(a,b,c,x,y))printf("无解\n");printf("%d*x + %d*y = %d的一些解是\n",a,b,c);printf("%d %d\n",x,y); //第一组for(int t = 2; t < 10; t++){ //输出其他的一些解int x1 = x + b/d*t;int y1 = y - a/d*t;printf("%d %d\n",x1,y1); //其余组}return 0;
}
唯一分解定理
(1)Aladdin and the Flying Carpet (素数打表+正整数的唯一分解定理,找因数对)
(2)GCD and LCM HDU - 4497(素数打表+唯一分解定理)求多少种情况
开关问题:
(1)D. 关灯问题(规律或二分)
(2)The Water Bowls POJ - 3185(开关问题+暴力)
(3)Fliptile POJ - 3279 (翻转)(二进制+对第一行暴力遍历翻转的位置)
尺取法
(1)Sum of Consecutive Prime Numbers POJ - 2739(线性欧拉筛+尺取法)
(2)Bound Found POJ - 2566(尺取法+前缀和创造区间变化趋势)
约瑟夫环
And Then There Was One POJ - 3517(变形约瑟夫环+规律)
阶乘
求阶乘的的位数
N的阶乘的长度(斯特林公式)
求阶乘最后非零数
Last non-zero Digit in N! HDU - 1066
数论相关公式
欧拉定理
对于互质的整数a和n,有aφ(n)≡1(moda^{φ(n)} ≡ 1(modaφ(n)≡1(mod n)n)n)
费马定理
a是不能被质数p整除的正整数,有a(p−1)≡1(moda^{(p-1)} ≡ 1(moda(p−1)≡1(mod p)p)p)
Polya定理
设G是p个对象的一个置换群,用k种颜色去染这p个对象,若一种染色方案在群G的作用下变为一种方案,则这两个方案当作是同一种方案,这样的不同染色方案数为:
L=1/∣G∣x∑(kC(f)),f∈GL = 1 / |G| x ∑(k^{C(f)}), f ∈ GL=1/∣G∣x∑(kC(f)),f∈G
C(f)为循环节,|G|表示群的置换方法数。
对于n个位置的手镯,有n种旋转置换和n种翻转置换。
对于旋转置换:
C(f[i]) = gcd(n, i),i表示旋转i颗宝石以后,i = 0时,gcd(n, 0) = n;
对于翻转置换:
如果n为偶数:则有n / 2个置换C(f) = n / 2,有n / 2个置换C(f) = n / 2 + 1;如果n为奇数:则有n个置换C(f) = n / 2 + 1。
欧拉函数 φ(n)
φ(n)积性函数,对于一个质数p和正整数k,有
φ(pk)=pk−p(k−1)=(p−1)p(k−1)=pk(1−1/p)φ(p^{k}) = p^{k} - p^{(k-1)} = (p - 1)p^{(k - 1) }= p^{k}(1 - 1 / p)φ(pk)=pk−p(k−1)=(p−1)p(k−1)=pk(1−1/p)
当n > 1时,1 … n中与n互质的整数和为nφ(n) / 2。
2n2^{n}2n 位数
len=(int)(n∗long10(2))+1,(2n−1同样适用)len=(int)(n∗long10(2))+1,(2^{n}−1同样适用)len=(int)(n∗long10(2))+1,(2n−1同样适用)
默慈金数 HVD 问题
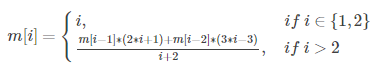
![[JavaWeb-JavaScript]JavaScript注释数据类型](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript注释数据类型)
)

![[JavaWeb-JavaScript]JavaScript变量](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript变量)
)


![[JavaWeb-JavaScript]JavaScript运算符](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript运算符)

)
![[JavaWeb-JavaScript]JavaScript特殊语法](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript特殊语法)

)
![[JavaWeb-JavaScript]JavaScript流程控制语句](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript流程控制语句)

![[JavaWeb-HTML]HTML概念介绍和快速入门](http://pic.xiahunao.cn/[JavaWeb-HTML]HTML概念介绍和快速入门)

![[JavaWeb-JavaScript]JavaScript_Function函数(方法)对象](http://pic.xiahunao.cn/[JavaWeb-JavaScript]JavaScript_Function函数(方法)对象)

