题目：

给出一个 nn 行 mm 列的矩阵，矩阵的每个位置有一个非负整数 a[i][j]，有 qq 次询问，每次询问求一个左上角为 (a,b)，右下角为 (c,d) 的子矩阵的所有数之和。

输入格式

第一行两个整数 n,m，表示矩阵的行和列的大小。

接下来 nn 行每行 m 个整数，为矩阵内容。

接下来一行为一个整数 q ，表示询问次数。

接下来 q 行每行 44 个整数 a,b,c,d，含义见题面。

输出格式

共 q 行，第 i 行为第 i个询问的答案。

数据范围
$n\times m\le 100,000，a[i][j]\le 1000，q\le 100,000，1\le a\le c\le n，1\le b\le d\le m。$

输出时每行末尾的多余空格，不影响答案正确性

要求使用「文件输入输出」的方式解题，输入文件为 sum.in，输出文件为 sum.out

样例输入

3 5
1 2 3 4 5
3 2 1 4 7
2 4 2 1 2
3
1 1 3 5
2 2 3 3
1 1 3 3

样例输出

43
9
20

分析：

1、先打表计算二维前缀和，再进行之后每次的查询。
2、需要使用数据结构vector存储数据。因为$n\times m\le 100,000$,要是开二维数组会爆，所以用vector容器存数据。

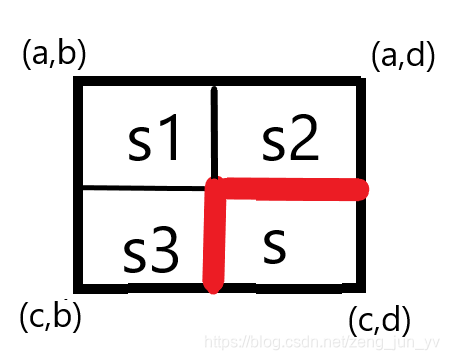
如图所示，假设要求S的话，可以用最大的矩形和减去S1+S2，再减去S1+S3，最后再加上S1即可。

AC代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
const int M=1e5+10;
const int inf=0x3f3f3f3f;
int n,m,k;
vector<int>mp[M];
int main(){freopen("sum.in", "r", stdin);freopen("sum.out", "w", stdout);scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){mp[i].push_back(0);for(int j=1;j<=m;j++){int x;scanf("%d",&x);mp[i].push_back(x);}}for(int i=0;i<=m;i++)mp[0].push_back(0);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)mp[i][j]+=mp[i-1][j]+mp[i][j-1]-mp[i-1][j-1];scanf("%d",&k);while(k--){int a,b,c,d;scanf("%d%d%d%d",&a,&b,&c,&d);int ans=mp[c][d]+mp[a-1][b-1]-mp[a-1][d]-mp[c][b-1];printf("%d\n",ans);}
}
/**
5 5
636 848 745 281 87
895 796 850 713 242
16 128 270 845 922
338 690 30 327 273
779 154 192 656 64
5
2 1  4 2
1 1  1 1
2 1  4 2
2 1  4 2
2 1  2 3
*/