​一般我们在解决立体几何题目时会选择建立坐标系，因为这样做比较保险也有固定套路。很多时候这些题目要求你计算某一个面的法向量（normal vector），这在高中阶段也是有固定方法的，我们这里想要介绍的是一种更高级也更迅速的方法，也就是引入向量叉乘（cross product，“向量”同物理中的“矢量”概念，一直想不通为啥数学和物理用不一样的名字，英文都是vector）这一概念。

我们都学过向量的标量积，也就是所谓的点乘（dot product），两个向量做标量积后得到的是一个标量。我们这里定义一种新的向量运算，也就是向量积或者叫叉乘:

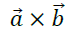
其运算结果仍是一个向量，我们记之为向量c，它的模定义为：

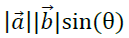
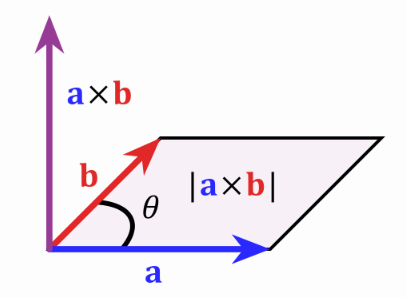
其中θ为向量a和向量b的夹角，如下图所示，c的模即以a和b为两条边的平行四边形的面积。

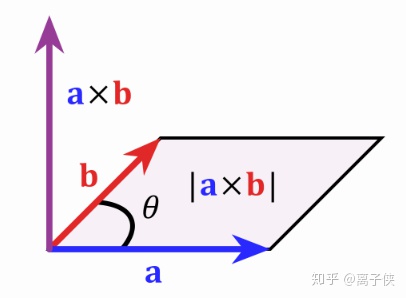
c的方向定义为垂直于a和b所构成的平面，并且a，b和c构成右手螺旋定则，也就是右手四指方向从a转向b，大拇指即得到c方向。定义了这一新的运算之后，我们从这个定义出发能证明以下几条重要性质：

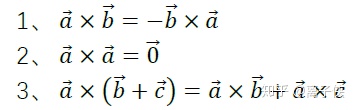
前两条性质根据定义一眼就能看出，第三条叉乘的分配律是非常重要的性质，证明也比较困难，我们不打算赘述了。

那么在三维坐标系中，a和b拥有了坐标表示后，c的坐标该怎么计算呢？记x，y，z轴正方向的单位向量分别为i，j，k，则有：

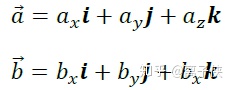
则根据叉乘的上述三条性质我们得到c为：

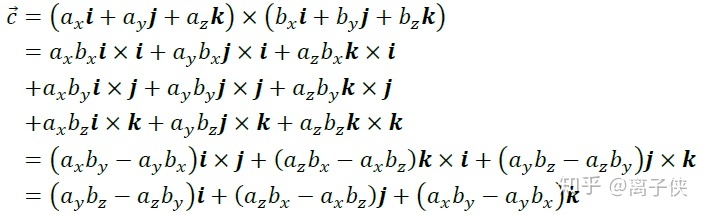
第二个等号我们运用了性质3，第三个等号我们运用了性质1和性质2，最后一个等号则运用了简单的i，j，k之间的叉乘关系。这一计算公式让我们直接能够从a和b的坐标表示得到c的坐标表示，用行列式可以更简洁地表示并方便记忆：

有了这个公式，对于任意一个面的法向量，我们总可以选取该面上的两个不共线向量来直接叉乘出来，一般解题中直接就选该面的两条边上的单位向量就行了。

警告：这个方法比高中阶段介绍的方程求解法要方便许多，但是用这种方法解题万一出错了很可能得不到求解法向量这一步的过程分。