算法设计与分析——回溯法—

算法设计与分析——回溯法——装载问题

0027算法笔记——【回溯法】回溯法与装载问题

自己写的代码：


#include <iostream>
using namespace std; template <class Type>
class Loading
{//friend Type MaxLoading(Type[],Type,int,int []);//private:public:void Backtrack(int i);int n,			//集装箱数*x,			//当前解*bestx;		//当前最优解Type *w,	//集装箱重量数组c,			//第一艘轮船的载重量cw,			//当前载重量bestw,		//当前最优载重量r;          //剩余集装箱重量
};//template <class Type>
//void  Loading <Type>::Backtrack (int i);template<class Type>
Type MaxLoading(Type w[], Type c, int n, int bestx[]);int main()
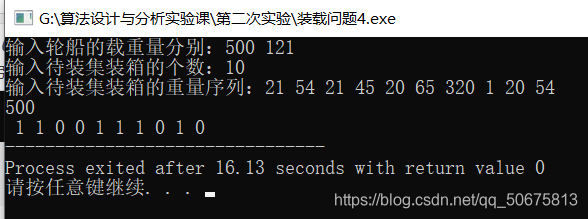
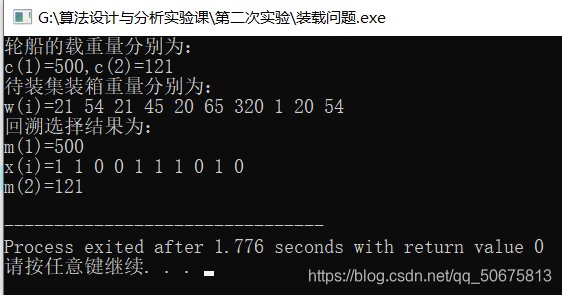
{   int n=10,m;int c=500,c2=121;int w[11]={ 0,21,54,21,45,20,65,320,1,20,54};int bestx[10];m=MaxLoading(w, c, n, bestx);cout<<"轮船的载重量分别为："<<endl;cout<<"c(1)="<<c<<",c(2)="<<c2<<endl;cout<<"待装集装箱重量分别为："<<endl;cout<<"w(i)=";for (int i=1;i<=n;i++){cout<<w[i]<<" ";}cout<<endl;cout<<"回溯选择结果为："<<endl;cout<<"m(1)="<<m<<endl;cout<<"x(i)=";for (int i=1;i<=n;i++){cout<<bestx[i]<<" ";}cout<<endl;int m2=0;for (int j=1;j<=n;j++){m2=m2+w[j]*(1-bestx[j]);}cout<<"m(2)="<<m2<<endl;if(m2>c2){cout<<"因为m(2)大于c(2),所以原问题无解！"<<endl;}return 0;
}template <class Type>
void  Loading <Type>::Backtrack (int i)// 搜索第i层结点
{if (i > n)// 到达叶结点{  if (cw>bestw){for(int j=1;j<=n;j++) {bestx[j]=x[j];//更新最优解bestw=cw; }} return;}r-=w[i]; if (cw + w[i] <= c) // 搜索左子树{ x[i] = 1;cw += w[i];Backtrack(i+1);cw-=w[i];    }if (cw + r > bestw){x[i] = 0;  // 搜索右子树Backtrack(i + 1);  }r+=w[i]; 
}template<class Type>
Type MaxLoading(Type w[], Type c, int n, int bestx[])//返回最优载重量
{Loading<Type>X;//初始化XX.x=new int[n+1];X.w=w;X.c=c;X.n=n;X.bestx=bestx;X.bestw=0;X.cw=0;//初始化rX.r=0;for (int i=1;i<=n;i++){X.r+=w[i];}X.Backtrack(1);delete []X.x;return X.bestw;
}

在这里插入图片描述
第二程序：

#include<iostream>
using namespace std;class Loading 
{public:int n;//当前集装箱的个数 //	int *x;//当前的解 int *bestx;//目前的最优解 int *w;//集装箱的重量数组 int c;//第一艘轮船的装载量 int cw;//当前的装载量 int bestw;//目前的最优装载量 //	int r;//剩余集装箱重量 void Backtrack(int i);//求第i层结点 }; 
void Loading::Backtrack(int i)//搜索第i层结点 
{if(i>n)//搜索到了叶子结点 {if(cw>bestw)//当前的载重量>目前最优载重量 {bestw= cw;}else{return ;} }else//还没有搜索到叶子结点时 {if(cw+w[i]<=c)//可以添加这个结点进入第一艘轮船，即左子树 {cw=cw+w[i];//需要在当前的载重量中加上该节点的重量 Backtrack(i+1);//搜索下一层cw=cw-w[i];// 必须放到这里面 ，如果不算这个节点时，需要将刚加上的w【i】减去 } // else 添加上这个else会出错  因为无论如何都要走右子树 //不添加这个结点进入第一艘轮船,即右子树 //{Backtrack(i+1);// } }
}int  MaxLoading(int w[],int c,int n)
{
//初始化 Loading  Loading X;X.w=w;X.c=c;X.n=n;X.bestw=0;X.cw=0;X.Backtrack(1);return X.bestw;} 
int main()
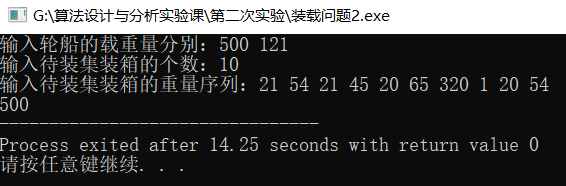
{cout<<"输入轮船的载重量分别：";int c1,c2;cin>>c1>>c2;cout<<"输入待装集装箱的个数：";int n;cin>>n;cout<<"输入待装集装箱的重量序列：";int w[n+1];for(int i=1;i<=n;i++){cin>>w[i];} cout<<MaxLoading( w,c1,n);
}

在这里插入图片描述
第三程序：

#include<iostream>
using namespace std;class Loading 
{public:int n;//当前集装箱的个数 //	int *x;//当前的解 int *bestx;//目前的最优解 int *w;//集装箱的重量数组 int c;//第一艘轮船的装载量 int cw;//当前的装载量 int bestw;//目前的最优装载量 int r;//剩余集装箱重量 void Backtrack(int i);//求第i层结点 }; 
void Loading::Backtrack(int i)//搜索第i层结点 
{if(i>n)//搜索到了叶子结点 {if(cw>bestw)//当前的载重量>目前最优载重量 {bestw= cw;}else{return ;} }else//还没有搜索到叶子结点时 {r-=w[i];//因为在初始化的时候就已经把该节点的重量加到了r中去了 if(cw+w[i]<=c)//可以添加这个结点进入第一艘轮船，即左子树 {cw=cw+w[i];//需要在当前的载重量中加上该节点的重量 Backtrack(i+1);//搜索下一层cw=cw-w[i];// 必须放到这里面 ，如果不算这个节点时，需要将刚加上的w【i】减去 } //不添加这个结点进入第一艘轮船,即右子树 if(cw+r>bestw)//剪枝函数 {Backtrack(i+1);}r+=w[i];//不管如何都要在加上这个w[i] }
}int  MaxLoading(int w[],int c,int n)
{
//初始化 Loading  Loading X;X.w=w;X.c=c;X.n=n;X.bestw=0;X.cw=0;X.r=0;for(int i=1;i<=n;i++){X.r+=w[i];} X.Backtrack(1);return X.bestw;} 
int main()
{cout<<"输入轮船的载重量分别：";int c1,c2;cin>>c1>>c2;cout<<"输入待装集装箱的个数：";int n;cin>>n;cout<<"输入待装集装箱的重量序列：";int w[n+1];for(int i=1;i<=n;i++){cin>>w[i];} cout<<MaxLoading( w,c1,n);
}

在这里插入图片描述
第四程序：
输出带有序列

#include<iostream>
using namespace std;
class Loading 
{public:int n;//集装箱的个数 int *w;//每个集装箱对应的重量 int c;//第一艘船的载重量int *x;//用于存储当前的解序列int *bestx;//用于存储目前的最优解 int bestw;//目前最优的载重量int cw;//当前的载重量 int r;//当前剩余的集装箱的重量 void Backtrack(int i); 	
};
void  Loading::Backtrack(int i)
{if(i>n)//搜索到了叶子结点 {if(cw>bestw)//当前的载重量>目前最优载重量 {for(int i=1;i<=n;i++){bestx[i] = x[i];}bestw= cw;}else{return ;} }else//还没有搜索到叶子结点时 {r-=w[i];//因为在初始化的时候就已经把该节点的重量加到了r中去了 if(cw+w[i]<=c)//可以添加这个结点进入第一艘轮船，即左子树 {x[i] = 1;cw=cw+w[i];//需要在当前的载重量中加上该节点的重量 Backtrack(i+1);//搜索下一层cw=cw-w[i];// 必须放到这里面 ，如果不算这个节点时，需要将刚加上的w【i】减去 } //不添加这个结点进入第一艘轮船,即右子树 if(cw+r>bestw)//剪枝函数 {x[i] = 0;Backtrack(i+1);}r+=w[i];//不管如何都要在加上这个w[i] }
}
int  MaxLoading(int n,int *w,int c,int *bestx)
{Loading X;X.n = n;X.w = w;X.bestx = bestx;X.c = c;X.bestw = 0;X.cw = 0;X.r = 0;X.x = new int [n+1];for(int i=1;i<=n;i++){X.r += w[i];}X.Backtrack(1);delete []X.x;return X.bestw;
}
int main()
{cout<<"输入轮船的载重量分别：";int c1,c2;cin>>c1>>c2;cout<<"输入待装集装箱的个数：";int n;cin>>n;cout<<"输入待装集装箱的重量序列：";int w[n+1];for(int i=1;i<=n;i++){cin>>w[i];} int bestx[n+1];int total_w=0;for(int i=1;i<=n;i++){total_w+=w[i];}if(total_w-MaxLoading( n,w,c1,bestx)>c2){cout<<"no solution"<<endl;return 0;}else{cout<<MaxLoading( n,w,c1,bestx)<<endl;for(int i=1;i<=n;i++){cout<<" "<<bestx[i];}}}