
通常,Nginx在安装完后,不用更改任何配置信息,我们就可以直接运行它。但是,这显然不能满足我们的生产要求。在生产中,要让Nginx能正常高效地运行我们的应用,我们通常需要对Nginx的配置文件进行一些参数上的设置,这就是所谓的Nginx调优。如下就是Nginx的一些重要配置,下面我们来详细介绍其中关键的两个:
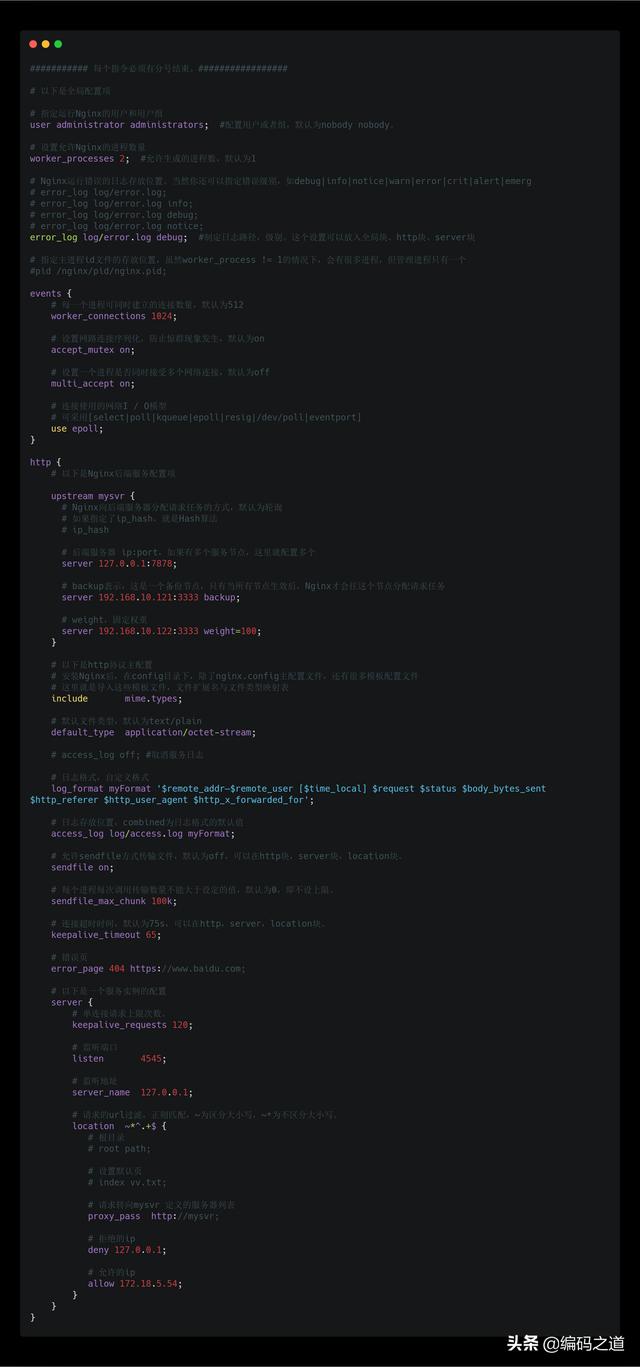
1、worker_processes
这个属性表示当操作系统启动时,有多少个工作进程将运行Nginx。
在Nginx运行时,系统会启动两种进程,一种是Master主进程,一种是Worker工作进程。主进程负责监控端口,协调工作进程的工作状态,分配工作任务;工作进程负责执行任务处理。通常,这个参数要设置成和操作系统的CPU内核数成倍数。因为,这样才能充分利用CPU的性能。
2、woker_connections
这个属性是指单个工作进程可以允许同时建立连接(无论这个连接是Nginx外部建立的,还是Nginx内部建立的)的数量。这里需要注意的是,一个工作进程建立一个连接后,进程将打开一个文件副本。所以,这个数量还与操作系统设定的进程最大可打开的文件副本数有关。
关于这一点,很多资料介绍说在修改worker_connections时,一定要是要ulimits -n修改操作系统对进程最大文件数的限制。但是实际操作发现,这样更改只能在当次用户的当次shell会话中起作用,并不是永久的。
那如何设置“进程最大可打开文件数”,并且永久有效?
这里有两步操作!
①更改操作系统“进程最大可打开文件数”的设置
首先,获取操作系统的root权限,然后修改limits.conf主配置文件:
vim /etc/security/limits.conf在主配置文件的最后加入下面两句:
* soft nofile 65535* hard nofile 65535soft:表示软件级别限制的最大可打开文件数的限制;hard:表示操作系统级别限制的最大可打开文件数的限制;*:表示所有用户都生效
保存这个文件后,配置是不会马上生效的,为了保证本次shell会话中的配置马上生效,我们需要通过ulimit命令更改本次的shell会话设置(或重启Linux操作系统):
ulimit -n 65535②更改Nginx软件“进程最大可打开文件数”的设置
以上操作,更改的只是操作系统级别的“进程最大可打开文件”的限制。对Nginx来说,还要对这个软件进行更改。打开nginx.conf主配置文件,配置worker_rlimit_nofile属性,如下:
worker_rlimit_nofile 65535;events {worker_connections 65535;}在生产环境下,我们一定要确保Nginx工作进程的配置信息是经过了优化设置的,否则,Nginx对并发请求的处理能力会大打折扣。










,切片,扩展,删除,追加,统计,长度,获取下标等...)








