
导读:
能量守恒定律告诉我们:能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一个物体转移到其它物体,而能量的总量保持不变。
熵作为只增不减的物质,该怎么去理解它?
通俗的理解熵:
举个栗子,对于这样一堆沙子,我们可以随意的更改沙堆的“形状”,甚至可以组成数万亿种形状,但不管哪种形状,构成沙子的“结构”不会发生任何改变,从熵的意义上讲,这个沙堆的熵值很高(这里的沙堆泛指一切自然形成的沙堆,大同小异)。

but,当我们把沙堆弄成这样一个沙堡:

这个时候,让一堆沙组成图中这种有规则形状的沙堡的组合就会骤降,甚至只有几种组合能让一堆沙看起来和图中的沙堡特别相似(沙子的结构仍然不会发生任何变化)。从熵的意义上讲,这个沙堡的熵值很低。
----------------------------------------
熵增又是怎样的情况呢?
说到熵增,我们都知道很多例子。比如理想气体扩散后不可能自己缩回去,温度只能自发从高温传到低温,这些都是熵增的过程。一句话,不可逆过程。
但问题是,这些不可逆过程发生的条件是什么?是不是在某些条件下可逆?
我来给大家举一个例子,一个熵自动减少的例子
好的。现在假设如下图所示一个密闭的长方体空间中有六个气体分子,一开始所有六个气体分子都被一个挡板压缩在长方体容器的左半边,现在挡板取消,分子开始扩散,充满整个容器,就像第二张图所显示的那样
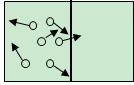
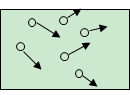
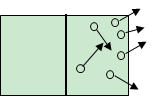
但是,如果我们适当规定一下气体分子的速度方向,就像上图那样,两个分子向左,四个分子向右,会发生什么情况呢?是的,我们会发现在某一个时刻,向左的两个分子碰壁后回弹,和向右的四个分子运动方向一致,最终这六个分子完全进入了右半空间。
这是气体自发的扩散,按定义熵增加,又自发地退回到右半边,按定义是熵减少。于是气体自发地熵先增加后减少!
再举一个最极端的例子。温度总是自发地由高温物体传向低温物体。在宏观世界不可想象低温物体自发传热给高温。但是当分子数目足够少的时候呢?
假设有三个分子组成的系统,动能分别为5,10,15焦耳,按照温度对应于分子平均动能的观点,它们的温度对应于平均动能10焦耳左右。另外也有三个分子组成的系统,完全一样的分子只是速度不一样,7,8,9焦耳。现在这两组分子被一个隔板分隔在长方体容器的两端。现在隔板去掉,让这两组分子发生碰撞,很有可能第一次碰撞就在动能为5的分子和这三个分子之间。假设是动能5焦耳和9焦耳发生碰撞,动量守恒交换交换速度,也同时交换能量,结果是原来5,10,15的系统变成了9,10,15;原来7,8,9的系统变成了7,8,5。这样,高温系统的分子平均动能更高了,低温系统的平均动能更低了,也就是高温更高,低温更低,热量自发地从低温传向高温。
现实中怎么可能!的确,在现实中我们费力吹起一个气球,用针一扎,只能看见气体自发地从气球里喷出,却从没有看到气体自发地回到气球里。如果我们不费力收拾我们的桌子,它们只会自发地越来越乱,从来没有看见它们自发地摆整齐过。
但是,如果我们桌子上只有两本书呢?哪怕我们不经意间随手一放,也有可能把原来摊在桌面上的两本书叠在一起。这样一来,熵又减少了。
不错,现在我们发现熵增的关键所在:分子数目。当我们在上面的体系中仅仅增加一两个分子的时候,情况似乎没有什么变化。我的桌子上摆了不管两本书还是三本书,似乎随手就可以把他们叠放在一起,不需要特别的整理。但是,当分子数目一个一个的增加,一直到标准状态下(零摄氏度,一个大气压下)在22.4升的容器里有个分子的时候,由量变积累的质变就发生了。
那么,这个质变是怎么发生的呢?
还是那个长方体空间里的例子。当挡板打开前,所有的分子都在左侧,当挡板打开后,所有的分子自由选择在长方体左边还是右边。所以,挡板打开后,所有的分子都重新回到右边的概率是也就是说1.56%的可能性,再加上全部重新回到左半边,一共是3.12%的概率气体重新回到整个容器的一半,即熵不变。虽然很小,但是有可能的。要知道,哪怕是所有分子都在左半边而只有一个分子在右半边也叫熵增。所以,当气体分子数目增加到个,那原先被限制在长方体左半边的气体扩散后又重新回到一半体积的概率是,可想而知和没有没区别。
但问题是,可不可以最终结果两边不同呢,还是那个长方体的例子,一开始左边是1000个分子,那最终结果可不可以是左边600个,右边四百个呢?看上去虽然两边都有,熵是增加了,但还没有到最大,这样可不可以呢?其实这种情况可以这样理解。在一个充满800个气体分子的长方体里,我们再从长方体左边加入两百个气体分子。那这两百个气体分子的运动不会受到其他气体分子运动的影响,也就是说,相当于原来真空的箱子里有两百个气体分子。结果呢,这多出的两百个还是会平分到两边,也就是两边都一样。
(当然,严格的数学意义表述是二项分布,这样得到的结果如下图所示,蓝线从外到内分别是长方体中含有10,40,70,100,130,160个分子时气体分子分布情况,横坐标表示长方体左侧所有气体分子数占总体分子数目的比例,纵坐标表示相对应分布的微观状态数,做了归一化处理,可以近似看成对应该微观状态的概率,可见分子数目足够多的时候,只有一种情况最常见最稳定,就是所有气体分子均匀分布)
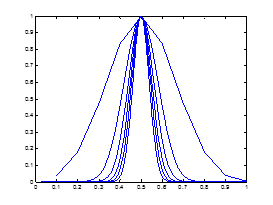
当然,我们允许长方体两边的气体分子有一个两个的差异,就好像在真空的长方体里只有两个分子的情况下我们也无法按照熵增加的要求要求这两个分子一定一个在左侧,一个在右侧。
熵增,这样一个在微观状态下完全由概率决定的事情,在宏观状态就成了必然。
因为熵自发减少的可能性是如此之小,以至于自从宇宙诞生到现在所有的分子运动的尝试中,始终无法找到一个幸运的系统或者分子能够自发的熵减。
一句话,熵之所以必然增加,没有动力或者能量的原因,是因为熵减少的概率,或者可能性小到可以忽略不计。
熵的微观失效宏观有效是统计力学系统微观量波动的本质。
----------------------------------------
为什么要引入熵这个概念?
19世纪,工程师在关注蒸汽机效率这个问题的时候,水要达到多热,要加入什么样的沸腾的物质才能让蒸汽机效率更高等等,为解答这些问题,热力学诞生了,并引入了热量、温度、能量等概念。并出现了热力学定律,这个时候的热力学定律是为了解释热量是如何流动。随着科学家了解深入,以及为了更好的理解宇宙进化及时间流逝,热力学第二定律出现了熵这个概念。
----------------------------------------
宇宙进化or时间流逝
回到我们上面的沙堆那个栗子里。如果我们把上图中的沙堡放在风中,很快这个沙堡中的沙粒会被风吹走,重新形成熵值更高的沙堆。在物理学原理里,没有哪条物理原理规定风不能将沙粒吹起,并精确的按照沙堡的形状摆放。从原则上说,风可以把沙粒吹起,并堆叠成一个沙堡。但它就是绝对不可能发生。而另一种可能性却不能避免,即风会将熵值很低的沙堡吹成熵值很高的沙堆。这吻合了热力学第二定律,也就是为什么可称之为“熵增定律”。正是熵增定律,解释了一切事物都是从有序趋向无序,也就说宇宙也是从有序走向无序,即xx亿年后,太阳也会从有序的球体爆炸为无序的气体和粉尘,即星云。
太阳的命运也说明了其它恒星的命运,即所有的恒星最终都会消亡,届时整个宇宙会陷入无边的黑暗,进而宇宙消亡。
来源:方兴、孙昊(知乎)


















)
)
