全世界只有3.14 % 的人关注了
数据与算法之美
死理性派的小编经常会被问到的一个问题:数学到底哪里有趣了,数学之美又在哪里?这篇文章精心选择了 10 个老少咸宜的算术问题,以定理、趣题甚至未解之谜等各种形式带领大家窥探数学世界的一角。不少问题背后都蕴含了深刻的数学知识,触及到数学的各个领域。希望从小数学就不及格的朋友们能够喜欢上数学这门充满乐趣的学科。推荐阅读《玩不够的数学》
数字黑洞 6174
任意选一个四位数(数字不能全相同),把所有数字从大到小排列,再把所有数字从小到大排列,用前者减去后者得到一个新的数。重复对新得到的数进行上述操作,7 步以内必然会得到 6174。
例如,选择四位数 6767:
7766 - 6677 = 1089 9810 - 0189 = 9621 9621 - 1269 = 8352 8532 - 2358 = 6174 7641 - 1467 = 6174 ……
6174 这个“黑洞”就叫做 Kaprekar 常数。对于三位数,也有一个数字黑洞——495。
3x + 1 问题
从任意一个正整数开始,重复对其进行下面的操作:如果这个数是偶数,把它除以 2 ;如果这个数是奇数,则把它扩大到原来的 3 倍后再加 1 。你会发现,序列最终总会变成 4, 2, 1, 4, 2, 1, … 的循环。
例如,所选的数是 67,根据上面的规则可以依次得到:
67, 202, 101, 304, 152, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
数学家们试了很多数,没有一个能逃脱“421 陷阱”。但是,是否对于 所有 的数,序列最终总会变成 4, 2, 1 循环呢?
这个问题可以说是一个“坑”——乍看之下,问题非常简单,突破口很多,于是数学家们纷纷往里面跳;殊不知进去容易出去难,不少数学家到死都没把这个问题搞出来。已经中招的数学家不计其数,这可以从 3x + 1 问题的各种别名看出来: 3x + 1 问题又叫 Collatz 猜想、 Syracuse 问题、 Kakutani 问题、 Hasse 算法、 Ulam 问题等等。后来,由于命名争议太大,干脆让谁都不沾光,直接叫做 3x + 1 问题算了。
直到现在,数学家们仍然没有证明,这个规律对于所有的数都成立。
特殊两位数乘法的速算
如果两个两位数的十位相同,个位数相加为 10,那么你可以立即说出这两个数的乘积。如果这两个数分别写作 AB 和 AC,那么它们的乘积的前两位就是 A 和 A + 1 的乘积,后两位就是 B 和 C 的乘积。
比如,47 和 43 的十位数相同,个位数之和为 10,因而它们乘积的前两位就是 4×(4 + 1)=20,后两位就是 7×3=21。也就是说,47×43=2021。
类似地,61×69=4209,86×84=7224,35×35=1225,等等。
这个速算方法背后的原因是,(10 x + y) (10 x + (10 - y)) = 100 x (x + 1) + y (10 - y) 对任意 x 和 y 都成立。
幻方中的幻“方”
一个“三阶幻方”是指把数字 1 到 9 填入 3×3 的方格,使得每一行、每一列和两条对角线的三个数之和正好都相同。下图就是一个三阶幻方,每条直线上的三个数之和都等于 15。
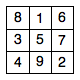
大家或许都听说过幻方这玩意儿,但不知道幻方中的一些美妙的性质。例如,任意一个三阶幻方都满足,各行所组成的三位数的平方和,等于各行逆序所组成的三位数的平方和。对于上图中的三阶幻方,就有:
816 2 + 357 2 + 492 2 = 618 2 + 753 2 + 294 2
利用线性代数,我们可以证明这个结论。
天然形成的幻方
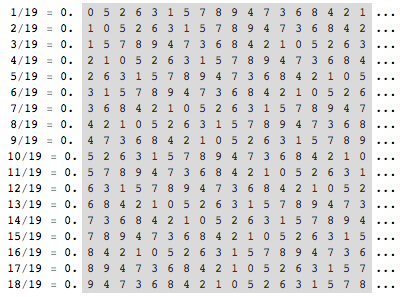
从 1/19 到 18/19 这 18 个分数的小数循环节长度都是 18。把这 18 个循环节排成一个 18×18 的数字阵,恰好构成一个幻方——每一行、每一列和两条对角线上的数字之和都是 81 (注:严格意义上说它不算幻方,因为方阵中有相同数字)。
196 算法
一个数正读反读都一样,我们就把它叫做“回文数”。随便选一个数,不断加上把它反过来写之后得到的数,直到得出一个回文数为止。例如,所选的数是 67,两步就可以得到一个回文数 484:
67 + 76 = 143 143 + 341 = 484
把 69 变成一个回文数则需要四步:
69 + 96 = 165 165 + 561 = 726 726 + 627 = 1353 1353 + 3531 = 4884
89 的“回文数之路”则特别长,要到第 24 步才会得到第一个回文数,8813200023188。
大家或许会想,不断地“一正一反相加”,最后总能得到一个回文数,这当然不足为奇了。事实情况也确实是这样——对于 几乎 所有的数,按照规则不断加下去,迟早会出现回文数。不过,196 却是一个相当引人注目的例外。数学家们已经用计算机算到了 3 亿多位数,都没有产生过一次回文数。从 196 出发,究竟能否加出回文数来?196 究竟特殊在哪儿?这至今仍是个谜。
Farey 序列
选取一个正整数 n。把所有分母不超过 n 的 最简 分数找出来,从小到大排序。这个分数序列就叫做 Farey 序列。例如,下面展示的就是 n = 7 时的 Farey 序列。
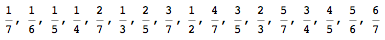
定理:在 Farey 序列中,对于任意两个相邻分数,先算出前者的分母乘以后者的分子,再算出前者的分子乘以后者的分母,则这两个乘积一定正好相差1 !
这个定理有从数论到图论的各种证明。甚至有一种证明方法巧妙地借助 Pick 定理,把它转换为了一个不证自明的几何问题!
唯一的解
经典数字谜题:用 1 到 9 组成一个九位数,使得这个数的第一位能被 1 整除,前两位组成的两位数能被 2 整除,前三位组成的三位数能被 3 整除,以此类推,一直到整个九位数能被 9 整除。
没错,真的有这样猛的数:381654729。其中 3 能被 1 整除,38 能被 2 整除,381 能被 3 整除,一直到整个数能被 9 整除。这个数既可以用整除的性质一步步推出来,也能利用计算机编程找到。
另一个有趣的事实是,在所有由 1 到 9 所组成的 362880 个不同的九位数中,381654729 是唯一一个满足要求的数!
数在变,数字不变
123456789 的两倍是 246913578,正好又是一个由 1 到 9 组成的数字。
246913578 的两倍是 493827156,正好又是一个由 1 到 9 组成的数字。
把 493827156 再翻一倍,987654312,依旧恰好由数字 1 到 9 组成的。
把 987654312 再翻一倍的话,将会得到一个 10 位数 1975308624,它里面仍然没有重复数字,恰好由 0 到 9 这 10 个数字组成。
再把 1975308624 翻一倍,这个数将变成 3950617248,依旧是由 0 到 9 组成的。
不过,这个规律却并不会一直持续下去。继续把 3950617248 翻一倍将会得到 7901234496,第一次出现了例外。
三个神奇的分数
1/49 化成小数后等于 0.0204081632 …,把小数点后的数字两位两位断开,前五个数依次是 2、4、8、16、32,每个数正好都是前一个数的两倍。
100/9899 等于 0.01010203050813213455 … ,两位两位断开后,每一个数正好都是前两个数之和(也即 Fibonacci 数列)。
而 100/9801 则等于
0.0102030405060708091011121314151617181920212223 … 。
利用组合数学中的“生成函数”可以完美地解释这些现象的产生原因。
作者:matrix67
来源:果壳
版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请留言联系删除,感谢合作。
 精品课程推荐:
精品课程推荐:


选购数学科普正版读物
严选“数学思维好物”
送给孩子的益智礼物 | 办公室神器
算法工程师成长阅读 | 居家高科技
理工科男女实用型礼物精选





数据与算法之美
用数据解决不可能

长按扫码关注

功能原理浅析)


)


)





=的安全处理)





