本文作者为 360 奇舞团前端开发工程师

引言

在使用 css 样式进行样式的缩放、旋转等设置时，思考了一下它的较浅层的原理，恩，这个阶段都 是一些初高的数学计算，从新看这里的时候顺便捡了捡初高中的数学，比如三角函数之类。

通用公式

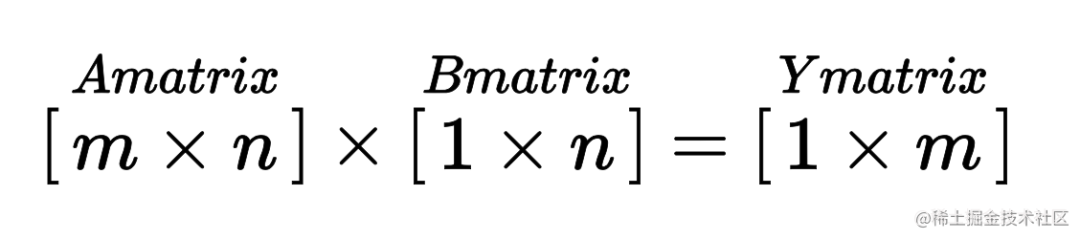
假设 A * B = Y。其中，A 为 m * n 的 m 行 n 列矩阵，B 为 1 * n 列的矩阵。B 拆分为列向量，并且列向量的维数就是矩阵的行数。

方法

transform(a, b, c, d, e, f) 与 Matrix 的转换。

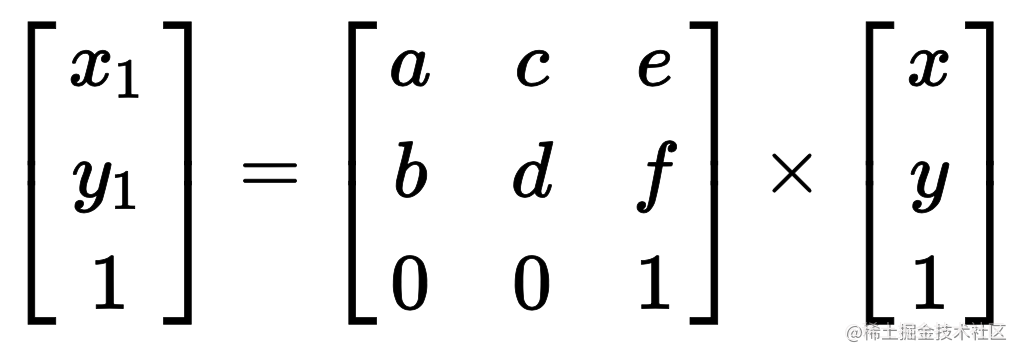
推导出来

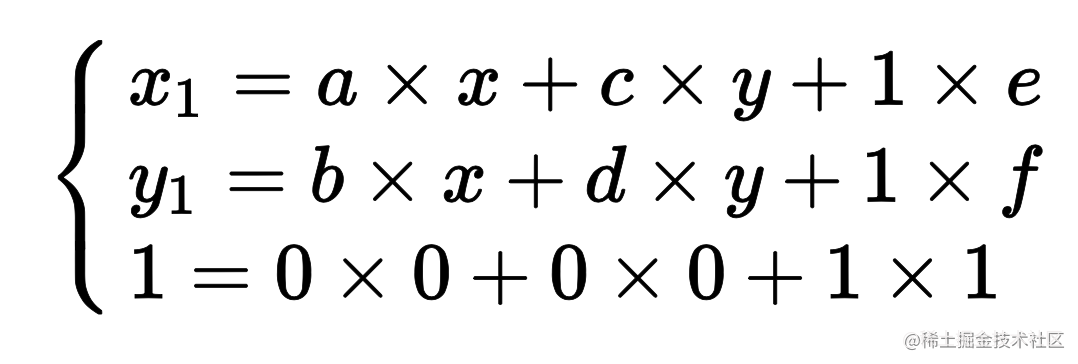
简化后

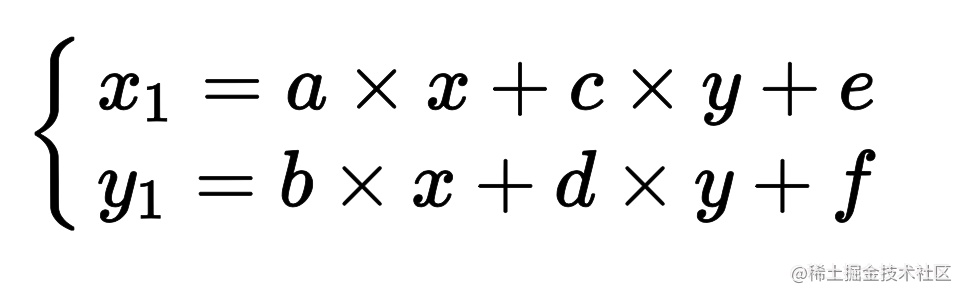
缩放

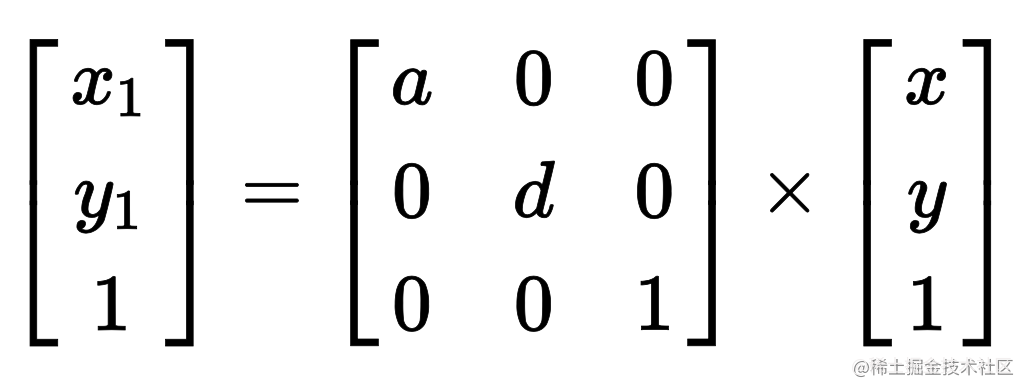
推导出来

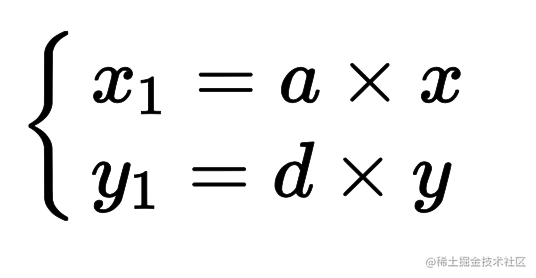
.box {transform: scale(0.3, 0.6);
}

通过计算

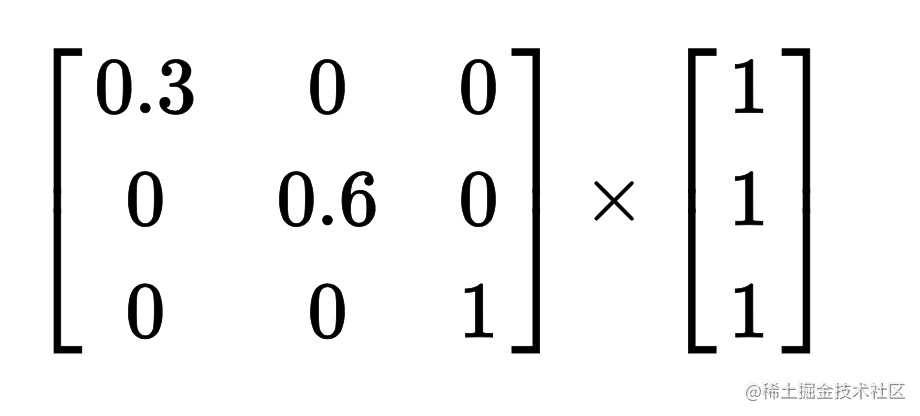
等价于

.box {transform: matrix(0.3, 0, 0, 0.6, 0, 0);
}

平移

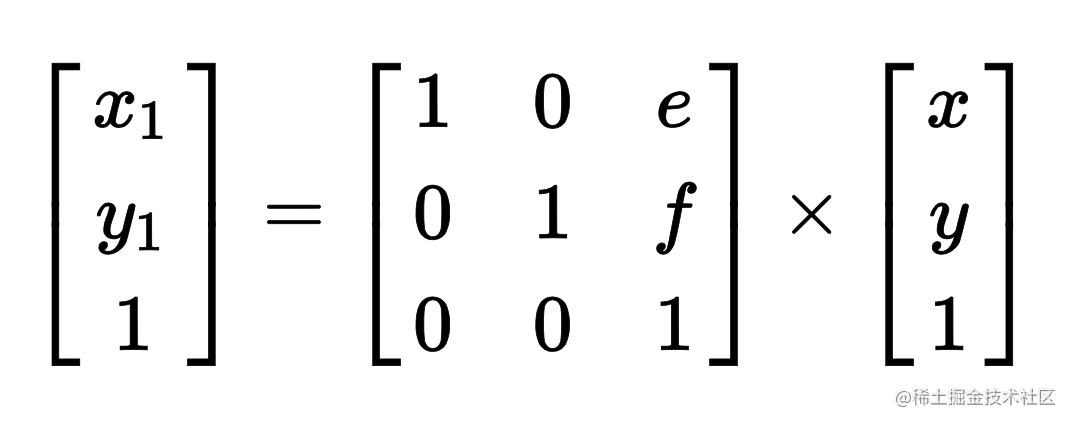
推导出来

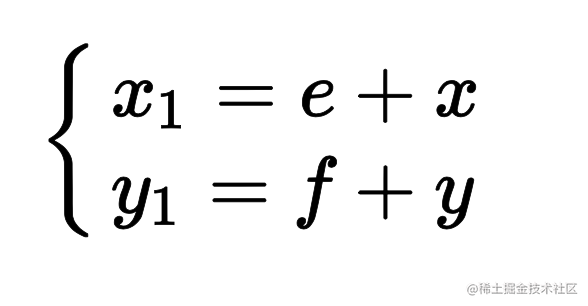
转旋

推导出来

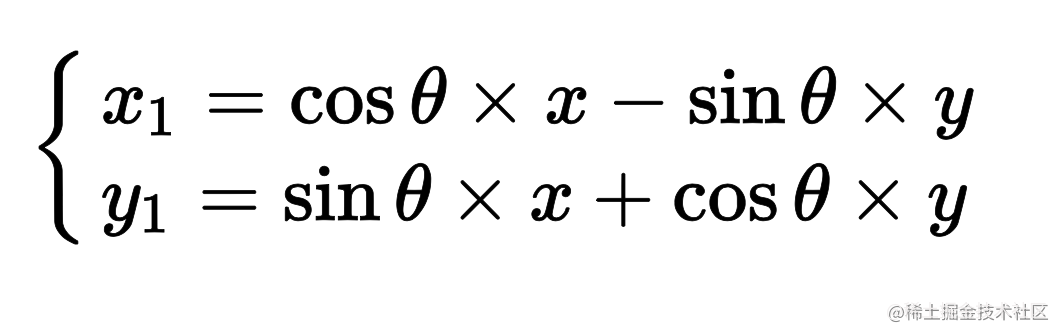
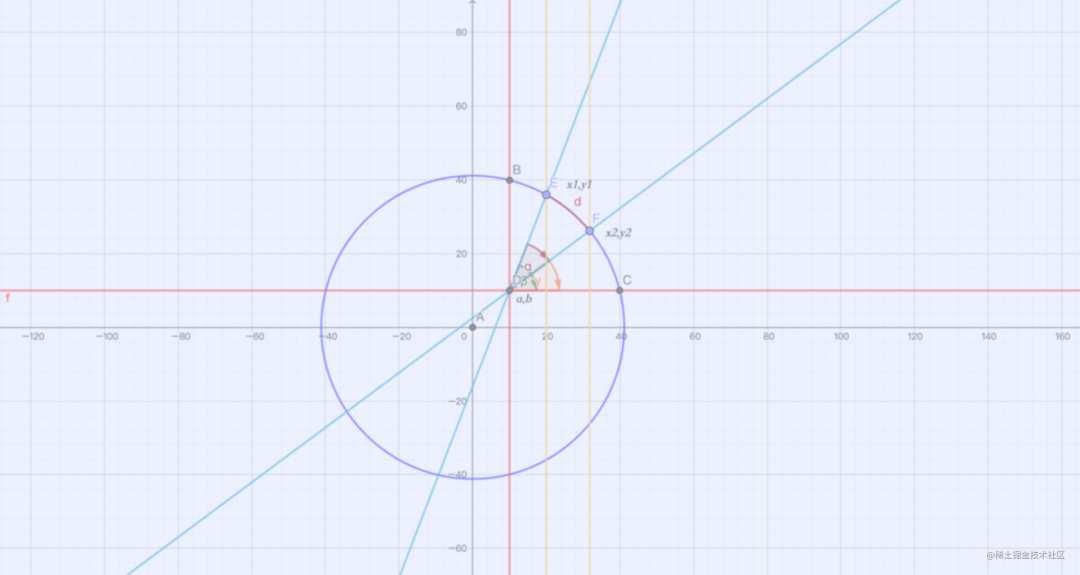
假设存在点 E 移动至点 F。设 E 坐标为(x1, y1)，F 坐标为(x2, y2)，D 坐标为(a, b)。

简要图示:

初中数学：

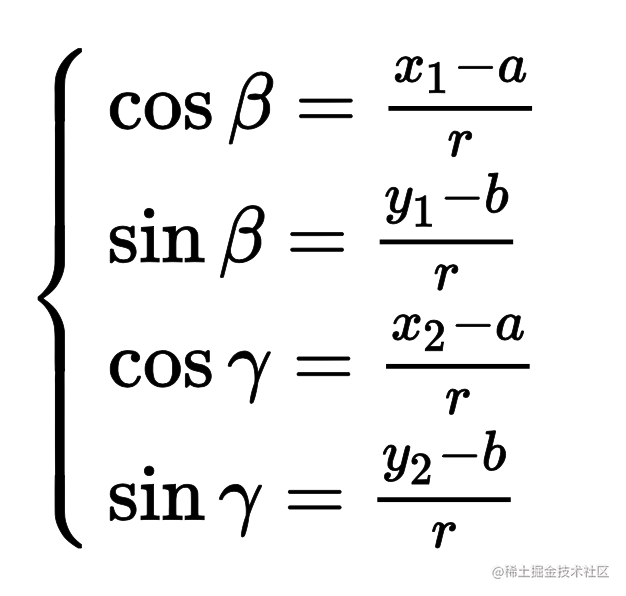
演算：

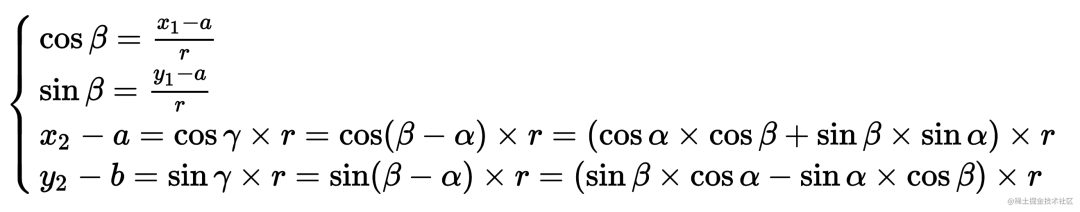
推导：

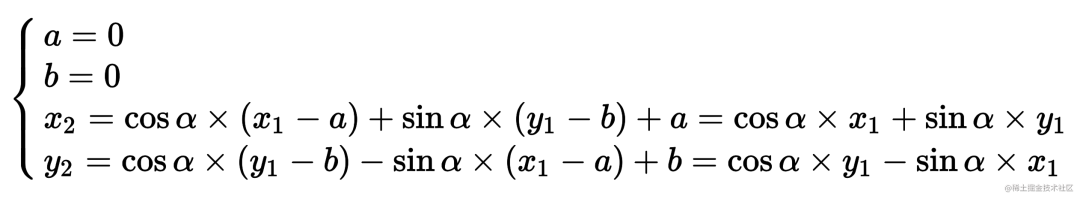
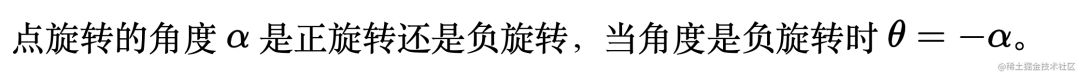
验证：

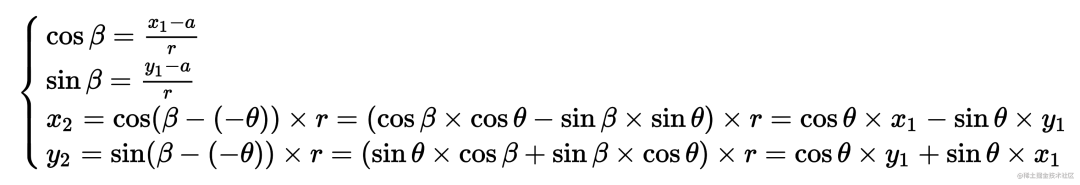
转换为矩阵：

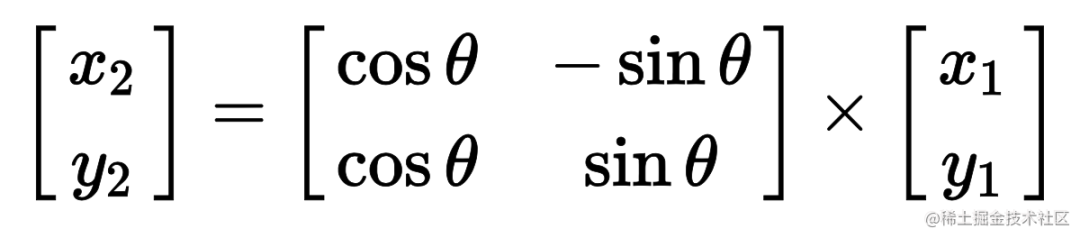
从 css 语法上开始转换

.box {transform: rotate(30deg);
}

这个旋转套用公式

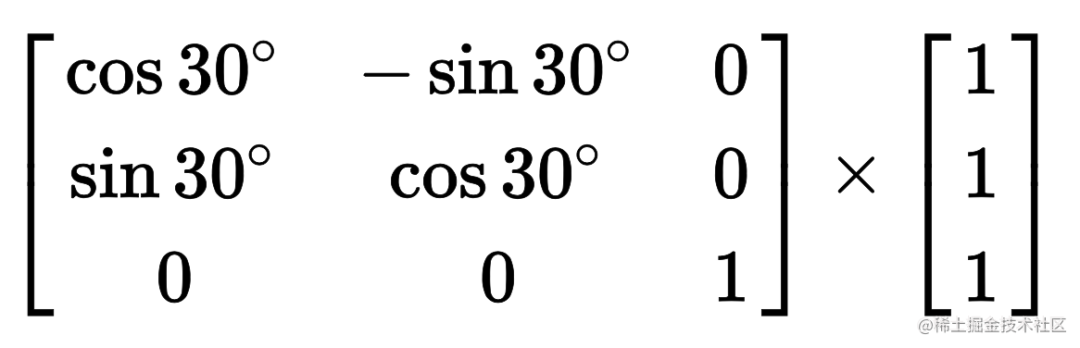
等价于

.box {transform: matrix(0.86, 0.5, -0.5, 0.86, 0, 0);
}

复合

.box {transform: rotate(30deg) scale(0.3, 0.6);
}

复合需要进行矩阵乘法计算

等价于

.box {transform: matrix(0.258, 0.15, -0.3, 0.516, 0, 0);
}

最后，后续本文修正和更新，请参阅：'https://kangkk.cn/index.php/计算机原理/仿射变换'

- END -

关于奇舞团

奇舞团是 360 集团最大的大前端团队，代表集团参与 W3C 和 ECMA 会员（TC39）工作。奇舞团非常重视人才培养，有工程师、讲师、翻译官、业务接口人、团队 Leader 等多种发展方向供员工选择，并辅以提供相应的技术力、专业力、通用力、领导力等培训课程。奇舞团以开放和求贤的心态欢迎各种优秀人才关注和加入奇舞团。