数据结构与算法(6) -- heap

binary heap就是一种complete binary tree(完全二叉树)。也就是说，整棵binary tree除了最底层的叶节点之外，都是满的。而最底层的叶节点由左至右又不得有空隙。

以上是一个对heap的简单介绍。本文将用heap指代此种完全二叉树。那么在实际编写代码的时候怎么组织这种数据呢，其实可以用array来存储这种结构的数据。将数组的第0个元素保留不用，从第一个元素开始存放数据。那么，对于树中的某个位于i的节点，其左子节点必然位于2i处，右子节点必然位于2i+1处，父节点必然位于“i/2”处。当然heap要能动态的改变大小，所以用vector存储数据会更好。

这里还有一个小的细节需要注意一下，heap可以分为max-heap以及min-heap，前者每个节点的键值都大于或等于其子节点键值，后者的每个节点键值都小于或等于其子节点键值。可以推出，max-heap的最大键值在根节点，min-heap的最小键值在根节点。

综上：heap就是一个包含了一组数据（通常可用array/vector来存储）以及一组管理这些数据的算法（插入元素，删除元素，取极值，将一组数据排列成一个heap）。通过这些方法可以保证heap的特性。

heap的算法

因为在c++ stl中并不直接提供heap这样一种数据结构，但它却是很多数据结构的基础：例如优先队列。所以这里我们主要关注的是heap涉及到的一些算法。

push_heap

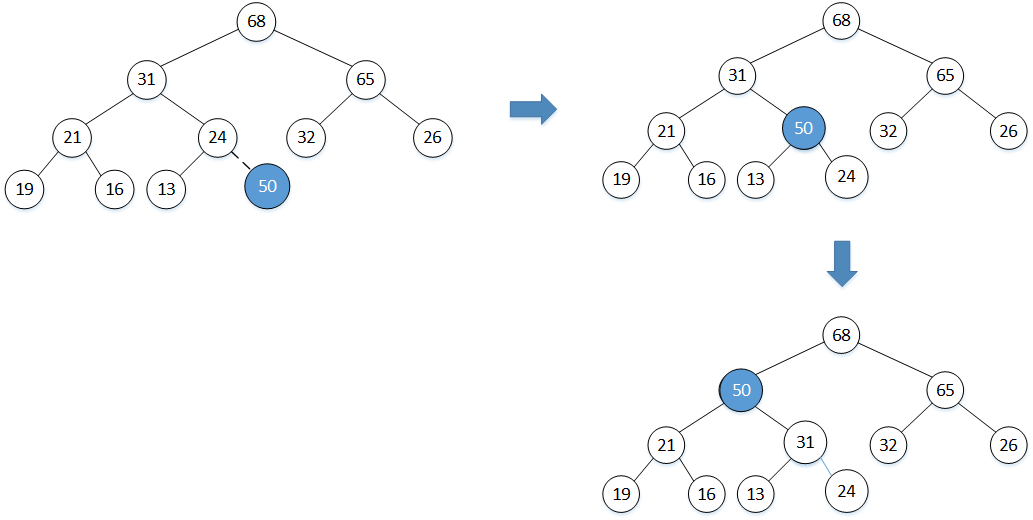
在很多书籍当中，通常通过一个上浮的操作来完成push_heap。其基本原理可见下图（假设新加入的元素是50）：

将50插入到数组的末尾。
将其于父元素相比较，发现24小于50，交换这两个元素。上浮一次
继续上述操作直到找到一个合适的位置，也即其父元素大于50的位置，则上浮结束。

一个简易的c++实现：

template<typename T>
void push_heap(std::vector<T> &vec, T value)
{vec.push_back(value);int i = vec.size()-1;while (i > 1 && vec[i] > vec[i / 2]) {std::swap(vec[i], vec[i / 2]);i = i / 2;}
}

pop_heap

pop操作是类似的：

将最后一个元素与第一个元素（根元素）交换。
删除最后一个元素。
将第一个元素/根元素下沉到一个合适的位置。注意下沉的时候是与子节点较大的那个元素交换。

一个简易的c++实现：

template<typename T>
T pop_heap(std::vector<T> &vec)
{int i = 1;//将最后元素与第一个元素(根元素)交换, 然后删除最后一个元素std::swap(vec[1], vec[vec.size() - 1]);T v = vec[vec.size() - 1];vec.pop_back();//将现在的第一个元素/根元素下沉到一个合适的位置while (2 * i < vec.size()) {int j = 2 * i;  //左子节点if (j < vec.size() - 1 && vec[j] < vec[j + 1]) j++;if (vec[j] < vec[i]) break;std::swap(vec[i], vec[j]);i = j;}return v;
}

sort_heap

sort_heap是利用heap每次都取出极值（这里是max）的特性进行排序。那么只要进行n次pop_heap即可完成排序。

template<typename T>
void sort_heap(std::vector<T> &vec)
{std::vector<T> temvec;int size = vec.size()-1;while (size != 0) {temvec.push_back(pop_heap(vec));size--;}for (T value : temvec) {vec.push_back(value);}
}