物流联合外包下库存管理模式对供应链运作的影响

作者：冯颖，林晴，张景雄，张炎治

 目录 

1 引言

2 问题描述

3 数学模型

4 协调模型

5 数值算例

6 结论

1 引言

传统库存管理模式下，供应链中各节点企业的库存管理各自为政，即节点企业各自运用自身的库存控制策略管理自有库存，库存管理相互封闭。寄售库存(CI)、供应商管理库存(VMI)等新型库存管理模式的出现，打破了传统库存管理各自为政的局面，充分体现供应链的协作理念。

本文的研究拟围绕以下三种库存管理模式展开：①传统的零售商管理库存(RMI)：零售商拥有库存决策权并按照实际订购量向供应商支付货款；②仅引入CI 的零售商管理寄售库存(RMCI)：零售商拥有库存决策权并按照实际销售量向供应商支付货款；③同时引入VMI和CI 的供应商管理寄售库存(VMCI)：供应商拥有库存决策权且零售商按照实际销售量向供应商支付货款。作者拟在物流联合外包情形下，探究上述三种库存管理模式对产运销供应链决策、运作以及合同设计的影响，并为供应链运作中库存管理模式的选取提供理论依据。

2 问题描述

考虑一个由单供应商、单TPLSP和单零售商组成的产运销供应链系统，系统在单周期内生产、运输和销售单一品种的产品，探究系统库存管理模式的变化对于其成员决策、运作效率以及合同设计的影响。依据实施 VMI或CI模式与否，可将供应商和零售商之间的库存管理模式划分为 RMI、RMCI和VMCI三种：

1)RMI(零售商管理库存)：预测终端市场需求D并据此决策订购量q，供应商按照零售商的订购量进行供给，零售商按照实际订购量向供应商转移支付货款T=wq；

2)RMCI(零售商管理寄售库存)：零售商按照实际订购量向供应商转移支付货款T=wEmin{q , D}；

3)VMCI(供应商管理寄售库存)：零售商按照实际订购量向供应商转移支付货款T=wEmin{q , D}；

本文拟基于上述三种库存管理模式，探究VMI和CI管理模式的引入对于供应链运作的影响，并以此为基础进行合同设计，以协调不同库存管理模式下的供应链系统。

以RMI模式为例，我们可采用图1来刻画供应链系统在一个产运销周期内的事件发生次序。

为使问题更加符合实际且便于运算，系统还需满足以下假设：

H1：市场需求具有递增的广义失败率(IGFR)特性；

H2：供应商的供给能力无限制；

H3：不考虑剩余产品的残值和缺货成本。

3 数学模型

3.1 不同库存管理模式下的分散决策模型

3.1.1 RMI 模式

RMI 模式下，处于强势地位的TPLSP为主导者，零售商和供应商为跟随者，三方进行序贯非合作博弈。根据问题描述，TPLSP向零售商和供应商收取的单位产品的物流服务费用为p ，故二者向TPLSP的转移支付为pq。首先，TPLSP基于反应函数q rm ( p )，决策最优物流服务价格p ：

随后，零售商在给定的物流服务价格p 下，决策最优订购量q，使得自身期望收益最大化。

令q 1 = a rg { q : L ( q ) = 1}，可得到定理1。

定理1：RMI 模式下，若市场需求满足IGFR特性，则系统存在唯一的博弈均衡解( q r m ， p r m )且满足：q rm Π( 0, q 1)。

定理1验证了RMI模式下，供应链系统博弈均衡解的存在性和唯一性，并给出了均衡的订购量满足的特定条件，其上限仅与需求函数的概率密度和概率分布相关。结合上述分析，进一步探讨均衡结果随零售商运费分摊比例、转移支付价格两个关键参数的变化，可得推论1：

推论1说明，RMI模式下，零售商的物流服务费用分摊比例及其向供应商的单位转移支付价格均会对系统成员决策和期望收益产生影响。

3.1.2 RMCI 模式

RMCI模式下的博弈过程同RMI模式，只是零售商向供应转支的货款变为R M C I=  w E m i n { q , D }，故改写式(1)~(3)，此时，供应商仍然无决策权，故采用逆向归纳法求解式(8)和(9)，可得定理2。

定理2：RMCI 模式下，若市场需求满足IGFR特性，则系统存在唯一的博弈均衡解( q r c， p r c )且满足：q rc  Î ( 0, q 1)。

定理2验证了RMCI模式下，供应链系统博弈均衡解的存在性和唯一性，其均衡的寄售量满足的区间条件同定理1 。

进一步探讨均衡结果随零售商运费分摊比例、转移支付价格两个关键参数的变化，可得推论2。

推论2说明，RMCI模式下，零售商的物流服务费用分摊比例j及其向供应商的单位转移支付价格w也会对系统成员决策和期望收益产生影响。

3.2 集中决策模式

集中决策模式下，零售商、TPLSP和供应商作为统一的决策体，共同决策q以使系统利润最大化。此时，供应链系统的期望收益模型如下：

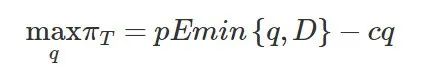
定理3：①pT是关于q的严格凹函数；②存在唯一的q，使系统期望收益pT达到最大，且满足：

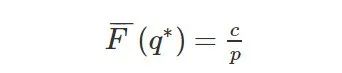
横向对比不同库存管理模式下的均衡结果和集中决策下的最优结果，可得到推论4。推论4表明，RMI模式下均衡的订购量一定低于RMCI模式下均衡的寄售量，这是因为CI模式的引入降低了零售商的订购风险，从而有效激励其提高订购量；同时，RMI模式下均衡的订购量一定低于集中决策下最优的订购量，这是由于分散决策降低了零售商订购的积极性所致。

4 协调模型

由于不同库存模式下的订购量/寄售量与集中决策的结果大小关系不明确，造成系统协调存在一定困难。以“利益共享、风险共担”为原则，同时参照业界实践，我们尝试在零售商和供应商之间引入具有双向调节作用的契约参数x(x>0,x¹1),当0<x<1时，为收入共享合同，即零售商把(1-x)*p*Emin(q,D)收入分给供应商，当x>1时为销售补贴合同,供应商给(x-1)*p*Emin(q,D)的收入分给零售商。

由上推导得推论6：在零售商和供应商之间引入销售补贴合同，可有效激励零售商提高订购量，进而实现供应链系统的完美协调。

推论7：当契约参数满足特定条件时，RMI模式下的系统能够实现帕累托改进，即实现各方成员共赢，从而确保了各方成员参与协调的主观意愿。

同RMI模式下，依次在RMCI、VMCI模式中引入双向调节契约，重写式(9)、(10)(16)和(17)，可得加入契约后的协调模型。采用类似推论6的证明方法，可得到系统实现完美协调的参数条件及取值情况如下表:

推论8：当契约参数满足特定条件时，RMCI和VMCI模式下的系统也能够实现帕累托改进。

5 数值算例

通过实际假设给参数赋值，代入上述模型，进行验算得出:

j的变化会影响系统各成员的期望收益，当j增加时，所有库存管理模式下零售商的期望收益均减少，而供应商的期望收益均增加。此外j的变化还会间接影响TPLSP的期望收益，当j增加时，RMI和RMCI模式下TPLSP的期望收益随之递减，而VMCI模式下其期望收益则随之递增，这与推论5一致。

w的变化对不同库存管理模 式下系统各成员及总的期望收益的影响与j变化的影响趋势大致相同，且计算结果与表2基本一致。

关于利润倾斜现象，较之于RMI模式，RMCI模式下的利润在w或j取值较小时会向零售 商和TPLSP倾斜，这是以牺牲供应商利益为代价的；VMCI模式下的利润在w或j取值较大时则会向供应商和TPLSP倾斜，而以牺牲零售商利益为代价。

6 结论

研究结果表明：RMI、RMCI和VMCI三种模式下的博弈均衡解均存在且唯一；RMI和RMCI模式下，均衡的订购量/寄售量随物流服务费用分摊比例j、单位转移支付价格w的增加而减少，VMCI模式则相反，即均衡的寄售量随这两个参数的增加而增加，这是由于库存决策权的转移造成的；RMI模式下，均衡状态下的系统总期望收益随物流服务费用分摊比例j、单位转移支付价格w的增加而减少，RMCI和VMCI模式下的系统总期望收益则随二者变化情况不明确。不同库存管理模式下，系统总的期望收益会出现不同程度的损失且系统总的期望收益与库存决策者的均衡订购量/寄售量密切相关。在零售商和供应商之间引入双向调节契约，通过调节契约参数的取值范围，可实现三种模式下的完美协调。

END

《中国管理科学》| 文章来源

蔡锦燕 吴雅洁 敖少良 普永康 | 文章解读

蔡锦燕 吴雅洁 敖少良 普永康 | 排排版版

朱小春 覃丹 | 审审核核