【跳台阶】有n级台阶，一个人每次上一级或者两级，问有多少种走完n级台阶的方法?

public int s1(int n){  if (n< 1){  return 0;  if(n == 1 || n== 2){   return n;   return s1(n - 1) +s1(n - 2);}

【最长递增子序列长度】给定数组arr，返回arr的最长递增子序列长度。比如arr=[2,1,5,3,6,4,8,9,7]，最长递增子序列为[1,3,4,8,9]，所以返回这个子序列的长度5。给定数组arr，返回arr的最长递增子序列长度。比如arr=[2,1,5,3,6,4,8,9,7]，最长递增子序列为[1,3,4,8,9]，所以返回这个子序列的长度5。

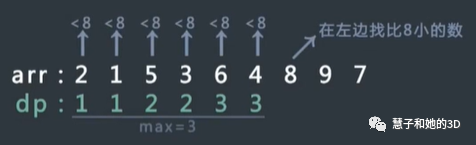
【解】先生成长度为5的数组dp，dp[i]表示在必须以arr[i]这个数结尾的情况下，arr[0..i]中的最大递增子序列长度。

arr[0]时，第一个最大递增子序列只有自己dp[0]=1；

接下来从左到右依次算出每个位置的数结尾的情况下最长递增子序列的长度。假设计算到位置i，求以i结尾的最长递增子序列长度，也就是dp[i]的值；如果最长递增子序列长度必须以arr[i]结尾,那么在arr[0……i-1]中所有比arr[i]小的数均可作为倒数第二个数，在这些数中，以哪个结尾的最长递增子序列长度最大选哪个作为倒数的第二个数；，故状态方程为arr[0……i-1]中所有数都不比arr[i]小，另dp[i]=1即可；说明必须以arr[i]结尾的最大递增子序列只包含arr[i]。

【最长公共子序列】给定两个字符串str1和str2，返回两个字符串的最长公共子序列。例如，str1="1A2C3D4B56"str2="B1D23CA45B6A”，”123456"或者"12C4B6"都是最长公共子序列，返回哪一个都行。

假设str1的长度为M, str2的长度为N，生成大小为M*N的矩阵dp.dp[i][j]的含义是str1[0..i]与str2[0..j]的最长公共子序列的长度。

dp求法如下:

        1、矩阵dp第一列，即dp[i][0]，代表str1[0..i]与str2[0]的最长公共子序列长度。str2[0]只有一个字符，所以dp[i][o]最大为1。

如果str1[i]==str2[0]，则令dp[i][0]为1一旦dp[i][0]被设为1，则令dp[i+i..M][0]全部为1

    2、矩阵dp第一行，即dp[0][j]，与步骤1同理。如果stri[0]==str2[j]，则令dp[0][j]为1，一且dp[0][j]被设为1,则令dp[0][j+1..N]全部为1

    3、其他位置，dp[i][jl的值只可能来自以下三种情况∶

    情况1∶可能是dp[i-1][j]的值。这代表str1[0..i-1]与str2[0..j]的最长公共子序列长度。

    举例:str1="A1BC2"，str2="AB34C".

str1[0..3]为”A1BC",str2[0..4]为”AB34C”，这两部分最长公共子序列为“ABC”，即dp[3][4]为3。str1整体和str2整体最长公共子序列也是"ABC”,所以dp[4][4]可能来自dp[3][4]。

    情况2∶同理可知，dp[i][]的值也可能是dp[i][j-1]。

    情况3:如果str1[i]==str2[j]，还可能是dp[i-1][j-1]+1的值。

    举例:比如str1="ABCD" ，str2="ABCD" .str1[0..2]即”ABC"与str2[0..2]即"ABC"的最长公共子序列为"ABC”，也就是dp[2][2]为3。因为str1和str2的最后一个字符都是”D”，所以dp[i][j]=dp[i-1][j-1]+1。

三种可能的值中，选最大值作为dp[i][j]的值。