数据结构在查找这一章里介绍过这些数据结构:BST,AVL,RBT,B和B+。
除去RBT,其他的数据结构之前的学过,都是在BST的基础上进行微小的限制。
1.比如AVL是要求任意节点的左右子树深度之差绝对值不大于1,由此引出插入删除等操作时的LL,RR,RL,LR旋转。
2.B树要求二叉树节点中保存的数据只有一个,而B-树得节点中保存的是线性表,真实数据数据不止一个有很多。由于表中的指针和子节点一一对应,而子节点个数又有限定(小于m但大于m/2)
3.B+树则是修改了B数里的规则,要求每个节点的关键字要出现在其对应子节点中。
废话少说,开始整理RBT,下面整理的内容是参考这篇文章的,很推荐去读一下。
1.RBT的基本定义
0.满足BST的要求
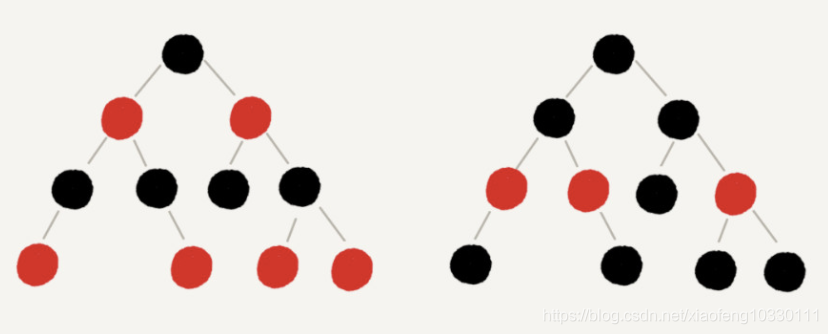
1.根节点和叶子节点是黑色的(叶子节点是空节点,下图中将null节点省略)
2.对于任意节点,从此节点到任何叶子节点的简单路径上的黑色节点数量一致。
3.只有红色和黑色两种颜色的节点
4.任意红色节点不相邻
顶端为黑,非红即黑,红不相邻,叶路黑同
2.RBT的插入
我们插入的节点一定为红色节点
情况1:插入为节点为a,其叔叔节点d为红色
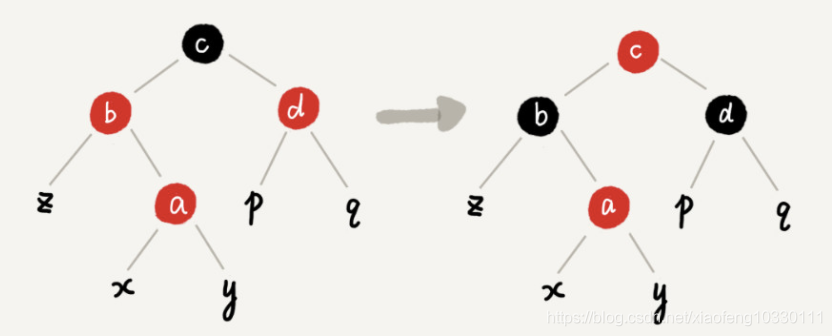
(这里注意,我们如果发现c其实是根节点的话,直接将b和d变成黑色)
改变之后还需要注意c父节点是否为红色,如果是则需要继续向上调整。
情况2:如果插入节点a是右孩子,它的叔叔节点 d 是黑色。
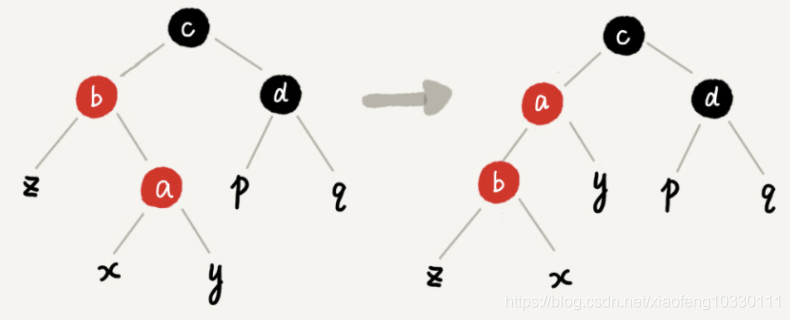
此时我们需要对a做一步左旋,然后进入情况三
情况3:插入点a为左子,叔叔节点为黑
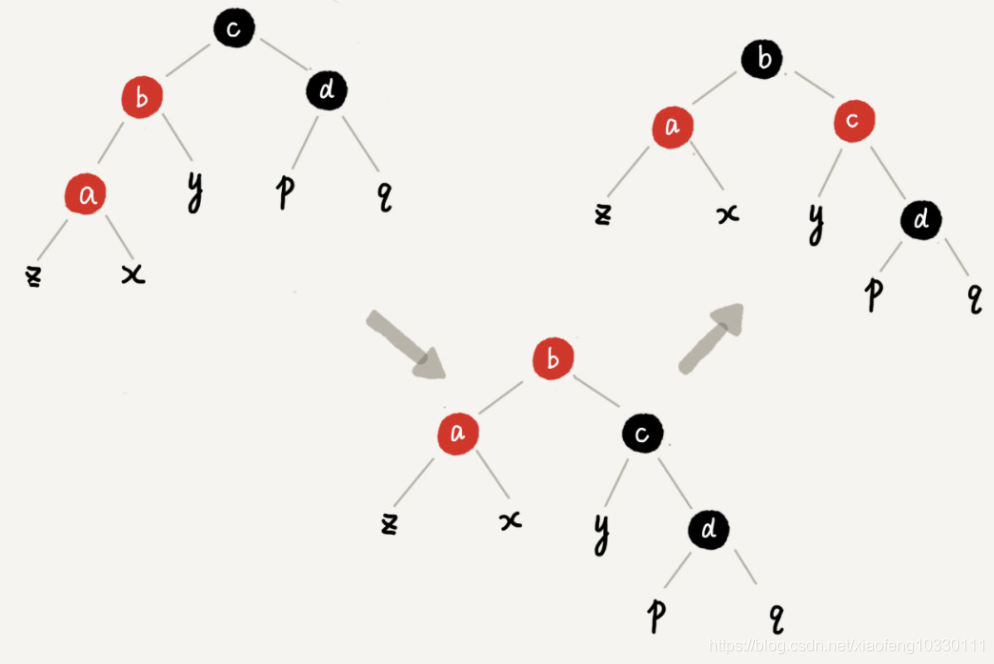
这样则是以b做右旋,然后交换b和c的颜色。
几个小技巧:
1.如何判断旋转类型:
我们从根节点向引发“事故”的节点走,连续两步就可以确定是LL,RR,LR,RL
2.怎么转。
LL是以不平衡子树的根节点,向右旋一次,RR则是向左旋。
LR是先以引发节点左旋一次,然后以根节点右旋一次,RL同理。
3.RBT的删除
为了保证满足红黑树定义的要求,有些节点会被标记成两种颜色,“红 - 黑”或者“黑 - 黑”。如果一个节点被标记为了“黑 - 黑”,那在计算黑色节点个数的时候,要算成两个黑色节点。
删除操作的平衡调整分为两步:
1.第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后,仍然满足最后一条定义的要求,也就是说,每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
2.第二步是针对关注节点进行二次调整,让它满足红黑树的第三条定义,即不存在相邻的两个红色节点。
初步调整
情况1:删除节点a,仅有一个子节点b
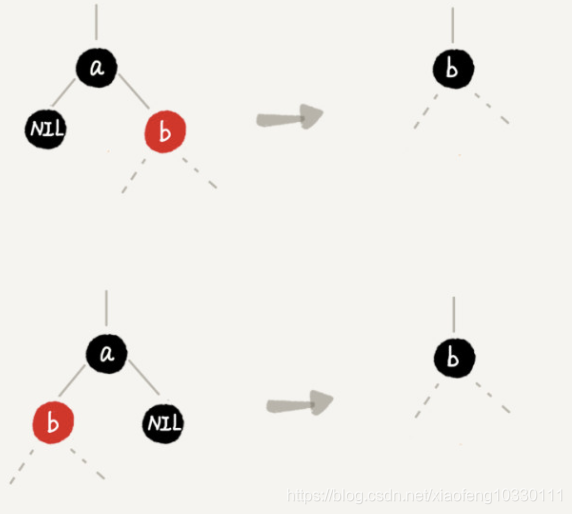
删除节点 a,并且把节点 b 替换到节点 a 的位置,改变b的颜色。
情况2:删除的节点 a 有两个非空子节点,并且它的后继节点就是节点 a 的右子节点 c
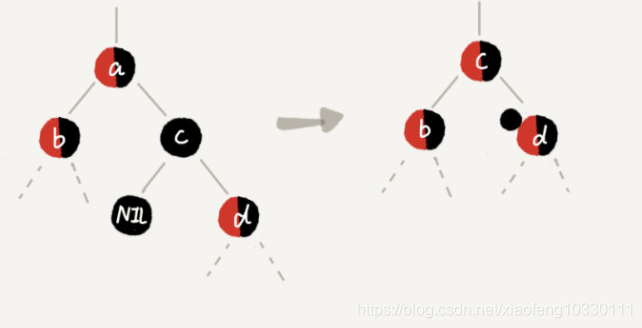
如果C无左子树,则删除a用c替代,c设置为与a相同的颜色,如果c原本为黑色,那么给c的子节点d多加一个黑色,变为“红 - 黑”或者“黑 - 黑”,这个时候,关注节点变成了节点 d,第二步的调整操作就会针对关注节点来做。
情况3:删除的是节点 a,它有两个非空子节点,并且节点 a 的后继节点不是右子节点
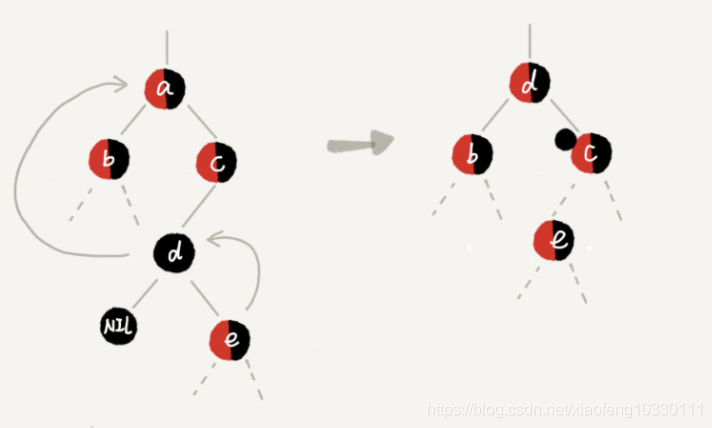
如果c有左子树,那么就让下一层的节点胜任后继节点,如果节点 d 是黑色,则c多加一个黑色标记。
二次调整
初步调整之后,关注节点变成了“红 - 黑”或者“黑 - 黑”节点。针对这个关注节点,再分四种情况来进行二次调整。
备注:二次调整是为了让红黑树中不存在相邻的红色节点。
情况1:如果带标记点是 a,它的兄弟节点 c 是红色的
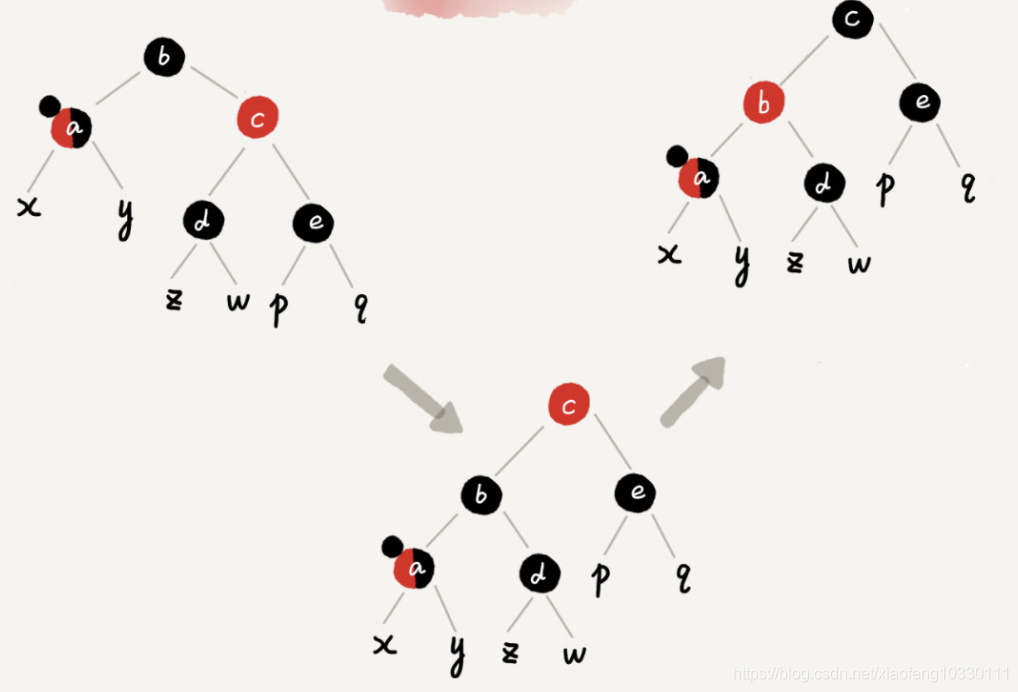
b左旋,然后标记节点和祖父节点c与父节点b交换颜色
情况2:如果带标记点是 a,它的兄弟节点 c 是黑色的,并且节点 c 的左右子节点 d、e 都是黑色的
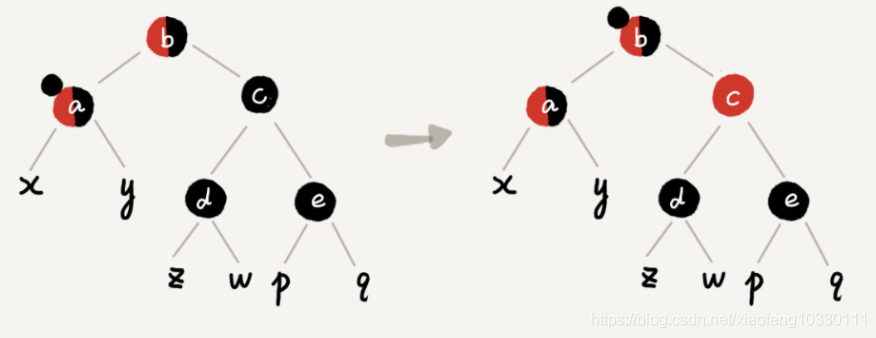
标记节点的兄弟c改为红色,a取消标记,父节点带标记。
前两种情况调整完后仍需找机会调整至第三种情况,然后转跳至第四种情况完成调整。
情况3:如果带标记点是 a,它的兄弟节点 c 是黑色,c 的左子节点 d 是红色,c 的右子节点 e 是黑色
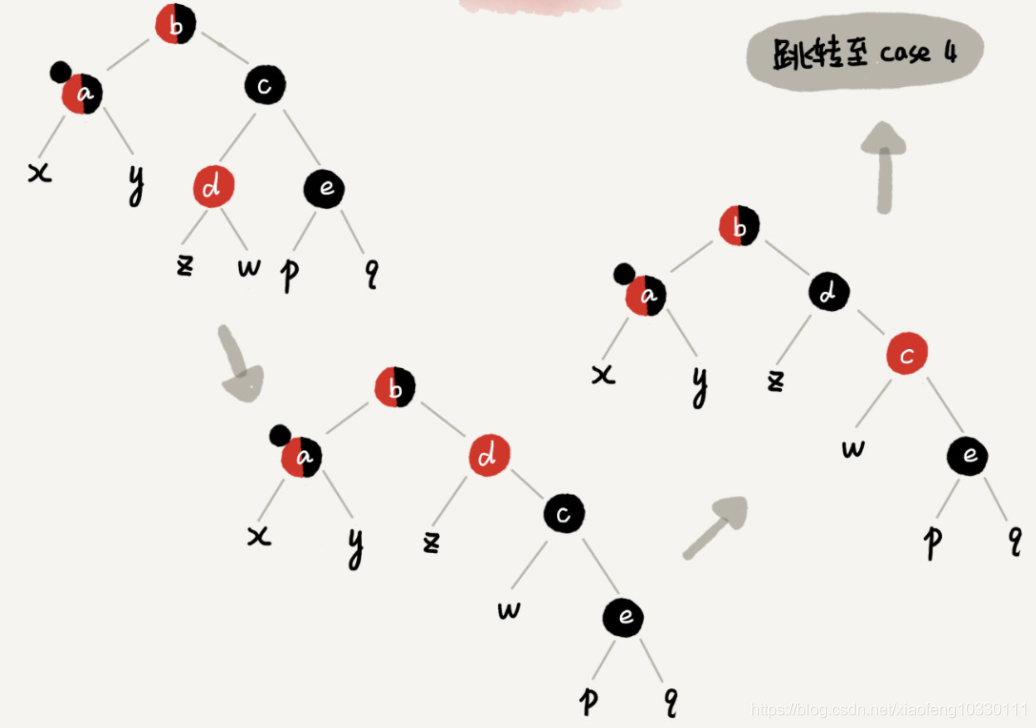
点 a 的兄弟节点 c 右旋;节点 c 和节点 d 交换颜色;转为第四种情况
情况4:如果带标记点 a 的兄弟节点 c 是黑色的,并且 c 的右子节点是红色的
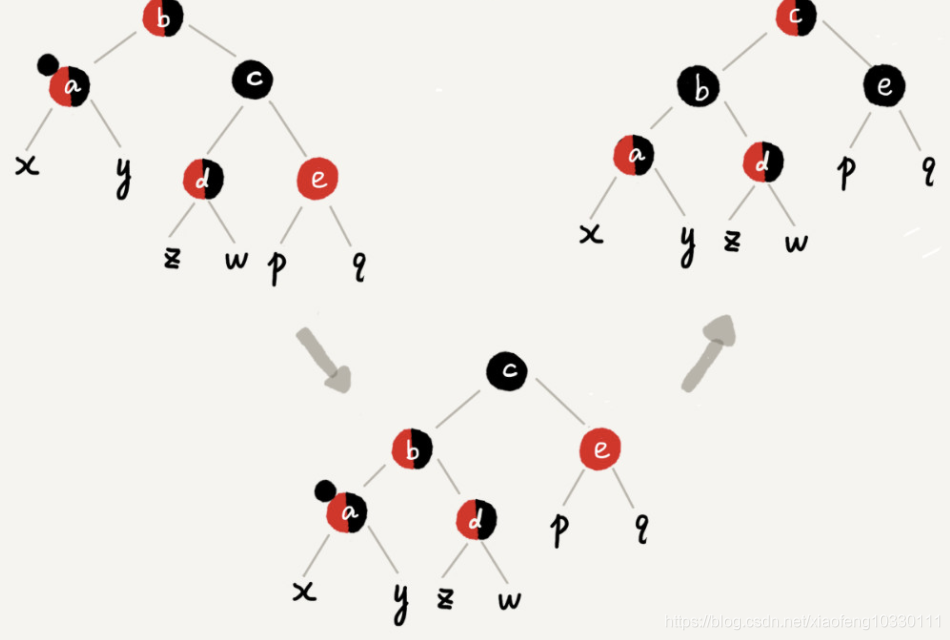
带标记节点a的父点 b 左旋;
将点 c 的颜色与点 b 设置成相同的颜色;
点 b 的颜色设置为黑色;
点 a 中去掉一个黑色,节点 a 就变成了红色或者黑色;
点 a 的叔叔节点 e 设置为黑色;
调整结束
我的妈啊,删除的第二步调整太复杂了!
写在后面的一点碎碎念
预推免面试时间紧迫,本想着两天吃透数据结构,结果发现自己有些痴心妄想了,两天复习下来发现了很多问题。
1.经常考察的十个排序里有很多忘记了具体实现。
2.查找这一章,我发现自己对B+,RBT基本不了解
3.图论这一章,我把AOE忘了
4.串串这一章的KMP虽然好学,但是这东西学一次忘一次。
5.绪论里很多基本概念不清楚,比如逻辑结构中线性结构的三个类型的典型代表的具体原理和实现然后计划如下:
1.如此看来完全搞好数据结构可能还需要3天左右,这3天里我会搞完数据结构,把之前复习好的操作系统和计算机网络巩固好不能忘记(短期计划)
2.然后是深度学习项目的很多理论知识忘了,我会坚持每天去学习机器学习基础和之前项目中的深度学习知识,对于机器学习基础,Fastrcnn,yolo,transformer和deepsort做到原理熟悉。(长期计划)
3.每天抽出时间去了解老师,套磁老师,准备面试需要的英语自我介绍和基本问题问答。(长期计划)




简单认识Wolfe Condition的收敛性证明)










![政府大数据资源中心建设总体方案[56页PPT]](http://pic.xiahunao.cn/政府大数据资源中心建设总体方案[56页PPT])



