目录
- 幂律（伽马）变换
幂律（伽马）变换
s=crγ(3.5)s = c r^{\gamma} \tag{3.5}s=crγ(3.5)
c和γc和\gammac和γ是正常数。考虑到偏移（即输入为0时的一个可度量输出），可改写为s=c(r+ϵ)γs = c (r + \epsilon) ^{\gamma}s=c(r+ϵ)γ
用于获取、打印和显示图像的许多设备的响应遵守幂律。用于校正这些幂律响应现象的处理称为伽马校正或伽马编码。
我们感兴趣的是曲线的形状，而不是它们的相对值
# 伽马变换不同伽马值的图像，为了图像好看，缩放到相同的数值范围
x = np.arange(0, 256, 1)
epsilon = 1e-5
gammas = [0.04, 0.10, 0.2, 0.40, 0.67, 1, 1.5, 2.5, 5.0, 10, 25]fig = plt.figure(figsize=(6, 6))
ax = fig.gca()
for gamma in gammas:n_power = normalize(np.power(x + epsilon, gamma)) * 255ax.plot(x, n_power, label='$\gamma = {}$'.format(gamma))ax.legend(loc='best')
plt.ylim([0, 255])
plt.xlim([0, 255])
plt.show()
def gamma_transform(img, c, gamma):"""gamma transform 2d grayscale image, convert uint image to floatparam: input img: input grayscale image param: input c: scale of the transformparam: input gamma: gamma value of the transoform"""img = img.astype(float) #先要把图像转换成为float，不然结果点不太相同epsilon = 1e-5 #非常小的值以防出现除0的情况img_dst = np.zeros(img.shape[:2], dtype=np.float)img_dst = c * np.power(img + epsilon, gamma)img_dst = np.uint8(normalize(img_dst) * 255)return img_dst
# 幂律（伽马）变换1
img = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0308(a)(fractured_spine).tif', 0)c = 1
gammas = [1.0, 0.04, 0.1, 0.3, 0.2, 0.4, 0.67, 0.9, 1.5, 2.5, 5, 10]
gama_len = len(gammas)fig = plt.figure(figsize=(15, 26))
for i in range(gama_len):ax = fig.add_subplot(4, 3, i+1, xticks=[], yticks=[])img_gamma= gamma_transform(img, c, gammas[i])ax.imshow(img_gamma, cmap='gray')if gammas[i] == 1.0:ax.set_title("Original")else:ax.set_title(f"$\gamma={gammas[i]}$")plt.tight_layout()
plt.show()
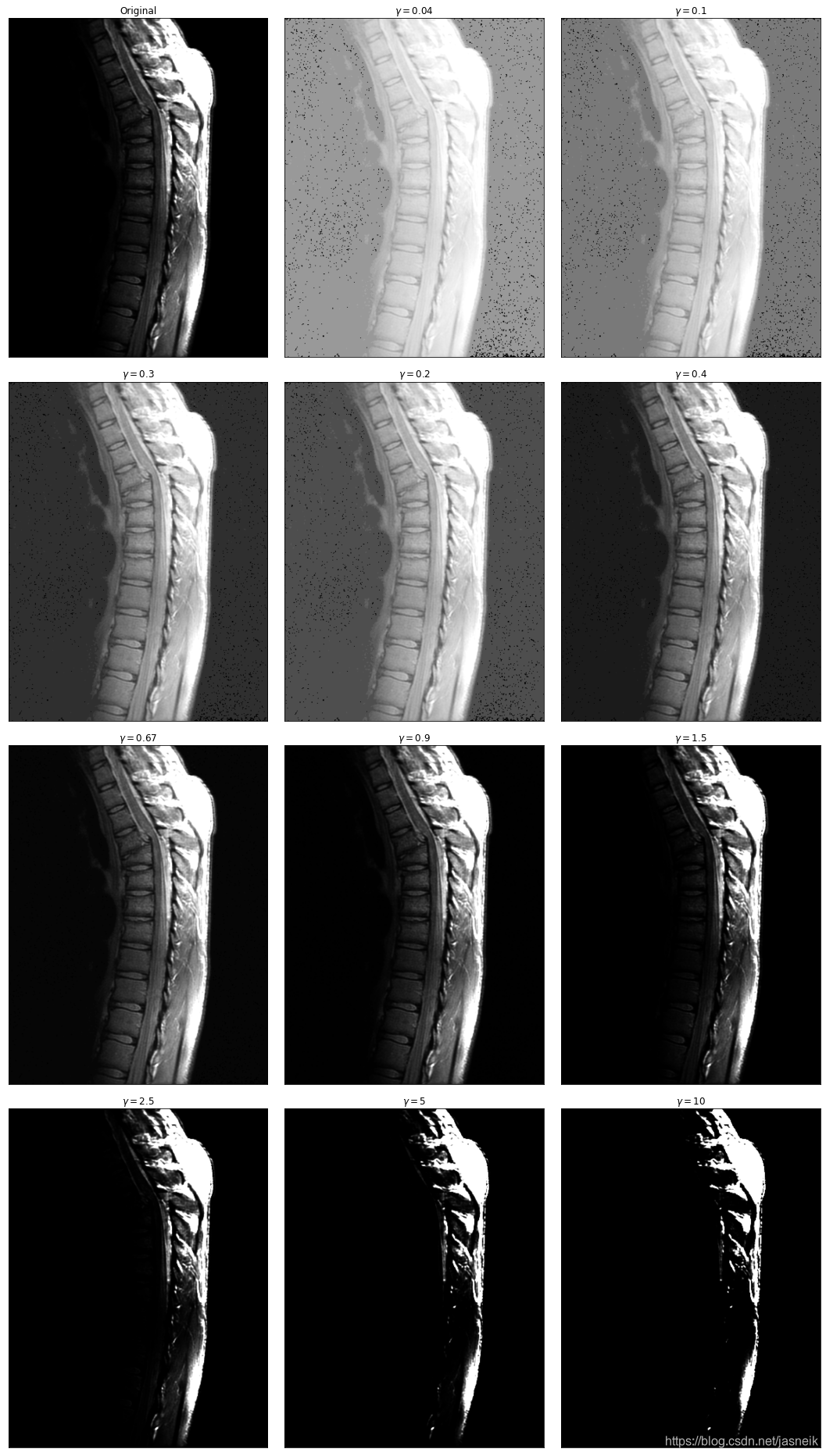
# 幂律（伽马）变换2
img = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0309(a)(washed_out_aerial_image).tif', 0)
c = 1
gammas = [1.0, 0.1, 0.3, 0.2, 0.4, 0.67, 0.9, 1.5, 3, 4, 5, 10]
gama_len = len(gammas)fig = plt.figure(figsize=(15, 21))
for i in range(gama_len):ax = fig.add_subplot(4, 3, i+1, xticks=[], yticks=[])img_gamma= gamma_transform(img, c, gammas[i])ax.imshow(img_gamma, cmap='gray')if gammas[i] == 1.0:ax.set_title("Original")else:ax.set_title(f"$\gamma={gammas[i]}$")plt.tight_layout()
plt.show()
