目录
- 直方图处理
直方图处理
令rk,k=0,1,2,…,L−1r_k, k=0, 1, 2, \dots, L-1rk,k=0,1,2,…,L−1表于一幅LLL级灰度数字图像f(x,y)f(x,y)f(x,y)的灰度。fff的非归一化直方图定义为：
h(rk)=nk,k=0,1,2,…,L−1(3.6)h(r_{k}) = n_{k}, \quad k = 0, 1, 2, \dots, L-1 \tag{3.6}h(rk)=nk,k=0,1,2,…,L−1(3.6)
nk是fn_{k}是fnk是f中灰度为rkr_{k}rk的像素的数量，并且细分的灰度级称为直方图容器。
归一化直方图
p(rk)=h(rk)MN=nkMN(3.7)p(r_{k}) = \frac{h(r_{k})}{MN} = \frac{n_{k}}{MN} \tag{3.7} p(rk)=MNh(rk)=MNnk(3.7)
def my_hist(img, bins=256, normalized=False):"""create a hist of uint8 image value range[0, 255]param: input img: grayscale image range[0, 255]param: input bins: bins for the image, range[0, 255]return hist and bins for the image, hist -> counts for all the values"""# initializ a list for values and countslist1 = list([x, y] for x in np.arange(bins) for y in np.arange(bins) if y == 0)data = img.flatten()for i in range(img.size):list1[data[i]][1] += 1 dst = np.array(list1)bins, hist= dst[:, 0], dst[:, 1]if normalized:hist = hist / img.size #nomalized histreturn hist, bins
# 直方图
img_1st = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(1)(top_left).tif', 0)
img_2nd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(2)(2nd_from_top).tif', 0)
img_3rd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(3)(third_from_top).tif', 0)
img_4th = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(4)(bottom_left).tif', 0)img_list =['img_1st', 'img_2nd', 'img_3rd', 'img_4th']fig = plt.figure(figsize=(20, 15))
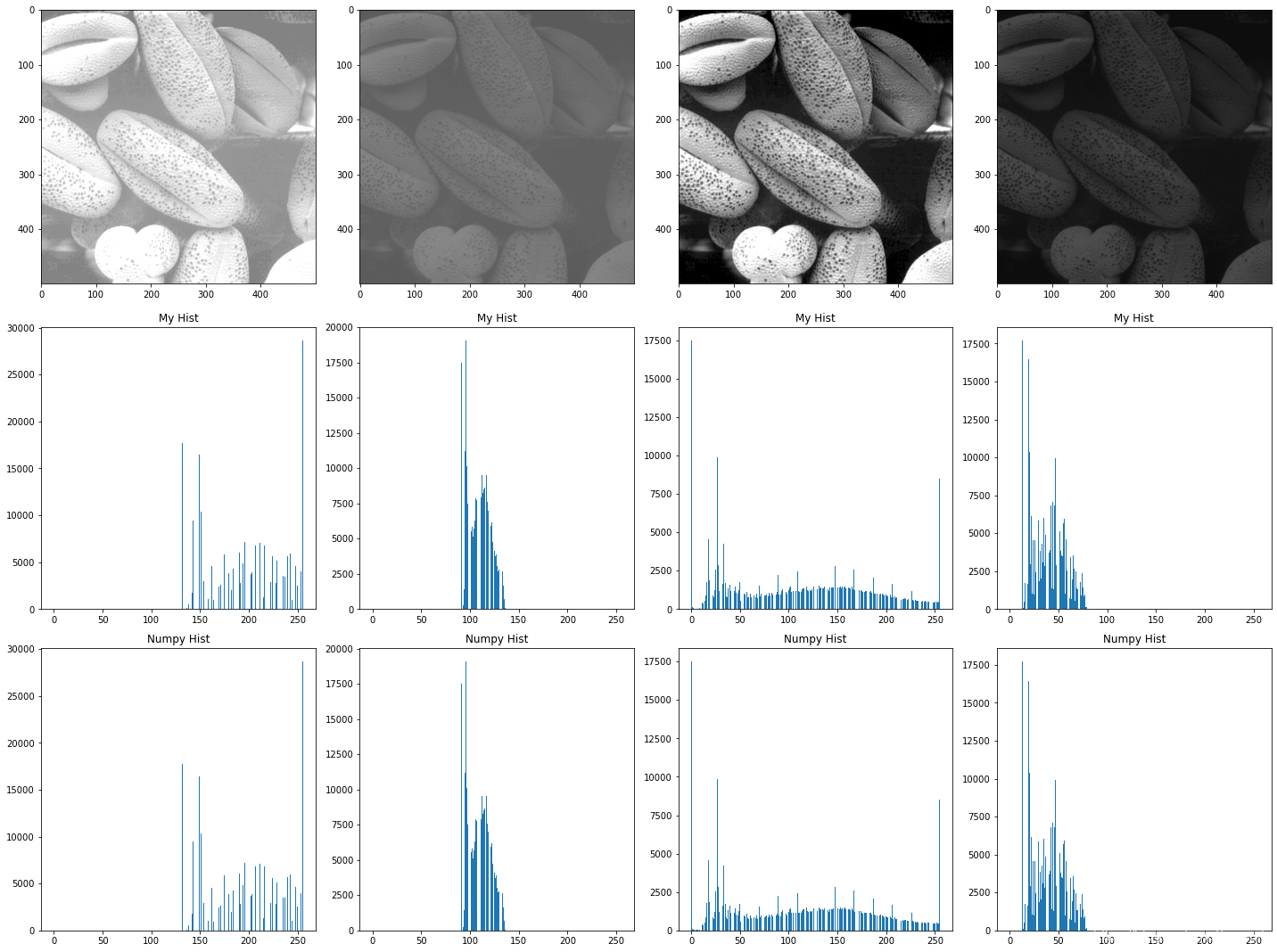
for i in range(len(img_list)):ax = fig.add_subplot(3, 4, i+1)ax.imshow(eval(img_list[i]), cmap='gray', vmin=0, vmax=255)ax1 = fig.add_subplot(3, 4, i+5)hist, bins = my_hist(eval(img_list[i]), bins=256)ax1.bar(bins, hist), ax1.set_title('My Hist')ax2 = fig.add_subplot(3, 4, i+9)hist, bins = np.histogram(eval(img_list[i]), bins=256, range=[0, 256])ax2.bar(bins[:-1], hist), ax2.set_title('Numpy Hist') # numpy 的返回bins 比hist多一点数，需要去掉最后一个
# ax2.hist(eval(img_list[i]).flatten(), bins=256, range=[0, 255]), ax2.set_title('Matplotlib Hist')
plt.tight_layout()
plt.show()
