直方图均衡化

• 灰度映射函数：
  $$s=T(r),0\le r\le L-1\text{\hspace{1em}(3.8)}$$

• 假设：

• (1) $T(r)$在区间$0\le r\le L-1$ 上是一个单调递增函数。

• (2) 对于$0\le r\le L-1$ ，有$0\le T(r)\le L-1$ 。

• 逆变换
  $$r=T^{-1}(s),0\le s\le L-1\text{\hspace{1em}(3.9)}$$

将条件(1)改为：

• (1’) $T(r)$在区间$0\le r\le L-1$ 上是一个严格单调递增函数。

(1)中$T(r)$单调递增的条件保证输出灰度值从不小于对应的输入值，从而防止灰度反转而产生伪像。
(2)保证输出灰度的范围与输入的范围相同。
(1’)保证从$s$返回到$r$的映射是一对一的，从而防止出现歧义。

图像的灰度可视为区间$[0,L-1]$内的一个随机变量。令$p_r(r)$和$p_s(s)$表示两幅不同图像中灰度值$r$和$s$的PDF（概率密度函数）。$p$的下标表明$p_r(r)$和$p_s(s)$是不同的函数。若已知$p_r(r)$和$T(r)$，且$T(r)$是连续的且在感兴趣的值域上是可微的，则变换（映射）后的变量$s$的PDF是
$$p_s(s)=p_r(r)\left|\frac{\text{d}r}{\text{d}s}\right|\text{\hspace{1em}(3.10)}$$
可以看到输出灰度变量$s$的PDF是由输入灰度的PDF和所有的变换函数确定的

图像处理中的一个特别重要的变换函数是
$$s=T(r)=(L-1){\int }_0^r{p}_r(w)\text{d}w\text{\hspace{1em}(3.11)}$$
$w$是一个假积分变量，右侧的积分是随机变量$r$的累积分布函数（CDF）

根据莱布尼茨积分法则可知
$$\frac{\text{d}r}{\text{d}s}=\frac{\text{d}T(r)}{\text{d}r}=(L-1)\frac{\text{d}}{\text{d}r}[{\int }_0^r{p}_r(w)\text{d}w]=(L-1)p_r(r)\text{\hspace{1em}(3.12)}$$
用这个结果代替式（3.10）的$\frac{\text{d}r}{\text{d}s}$，并且所有的概率值都是正的，有：
$$p_s(s)=p_r(r)\left|\frac{\text{d}r}{\text{d}s}\right|=p_r(r)\left|\frac{1}{(L-1)p_r(r)}\right|=\frac{1}{L-1},0\le s\le L-1\text{\hspace{1em}(3.10)}$$

直方图均衡化或直方图线性变换
式（3.11)变换的离散形式为：
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j),k=0,1,2,\dots ,L-1\text{\hspace{1em}(3.15)}$$

def my_calhist(img):"""histogram equalizationparam: input img: uint8[0, 255] grayscale imagereturn uint8[0, 255] grayscale image after histogram equalization"""hist, bins = my_hist(img, bins=256, normalized=True)#--------------------------------Numpy-------------------hist_cumsum = np.round(np.cumsum(hist) * 255).astype(int)img_dst = img.copy()img_dst = hist_cumsum[img_dst]#--------------------------------loop----------------------
#     map_dict = {}
#     map_dict = map_dict.fromkeys(bins.astype(int), 0)    
#     for i in bins:
#         s = np.round(255 * hist[:i].sum()).astype(int)
#         map_dict[i] = s#     height, width = img.shape[:2]
#     img_dst = np.zeros([height, width], np.uint8)
#     for h in range(height):
#         for w in range(width):
#             img_dst[h, w] = map_dict[img[h, w]] # dict 用[ ]
#     img_dst = np.clip(img_dst, 0, 255).astype(np.uint8)
#     return img_dst, map_dict         return img_dst, _

# 直方图均衡化
import time
img_1st = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(1)(top_left).tif', 0)
img_2nd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(2)(2nd_from_top).tif', 0)
img_3rd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(3)(third_from_top).tif', 0)
img_4th = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(4)(bottom_left).tif', 0)img_list =['img_1st', 'img_2nd', 'img_3rd', 'img_4th']fig = plt.figure(figsize=(20, 20))
start_time = time.time()
for i in range(len(img_list)):# plot orginal imageax = fig.add_subplot(4, 4, i+1)ax.imshow(eval(img_list[i]), cmap='gray', vmin=0, vmax=255), ax.set_title('Original')# plot histogram equalization imageimg_dst, _ = my_calhist(eval(img_list[i]))ax1 = fig.add_subplot(4, 4, i+5)ax1.imshow(img_dst, cmap='gray', vmin=0, vmax=255), ax1.set_title('After Histogram Equalization')# plot orginal histax2 = fig.add_subplot(4, 4, i+9)hist, bins = my_hist(eval(img_list[i]), bins=256)ax2.bar(bins, hist), ax2.set_title('Original Histogram')# plot hist after histogram equalizationax3 = fig.add_subplot(4, 4, i+13)hist, bins = my_hist(img_dst, bins=256)ax3.bar(bins, hist), ax3.set_title('Hist After Histogram Equalization')elapse = time.time() - start_time
print(f'Elapse -> {elapse}s') 
plt.tight_layout()
plt.show()

Elapse -> 2.3357810974121094s

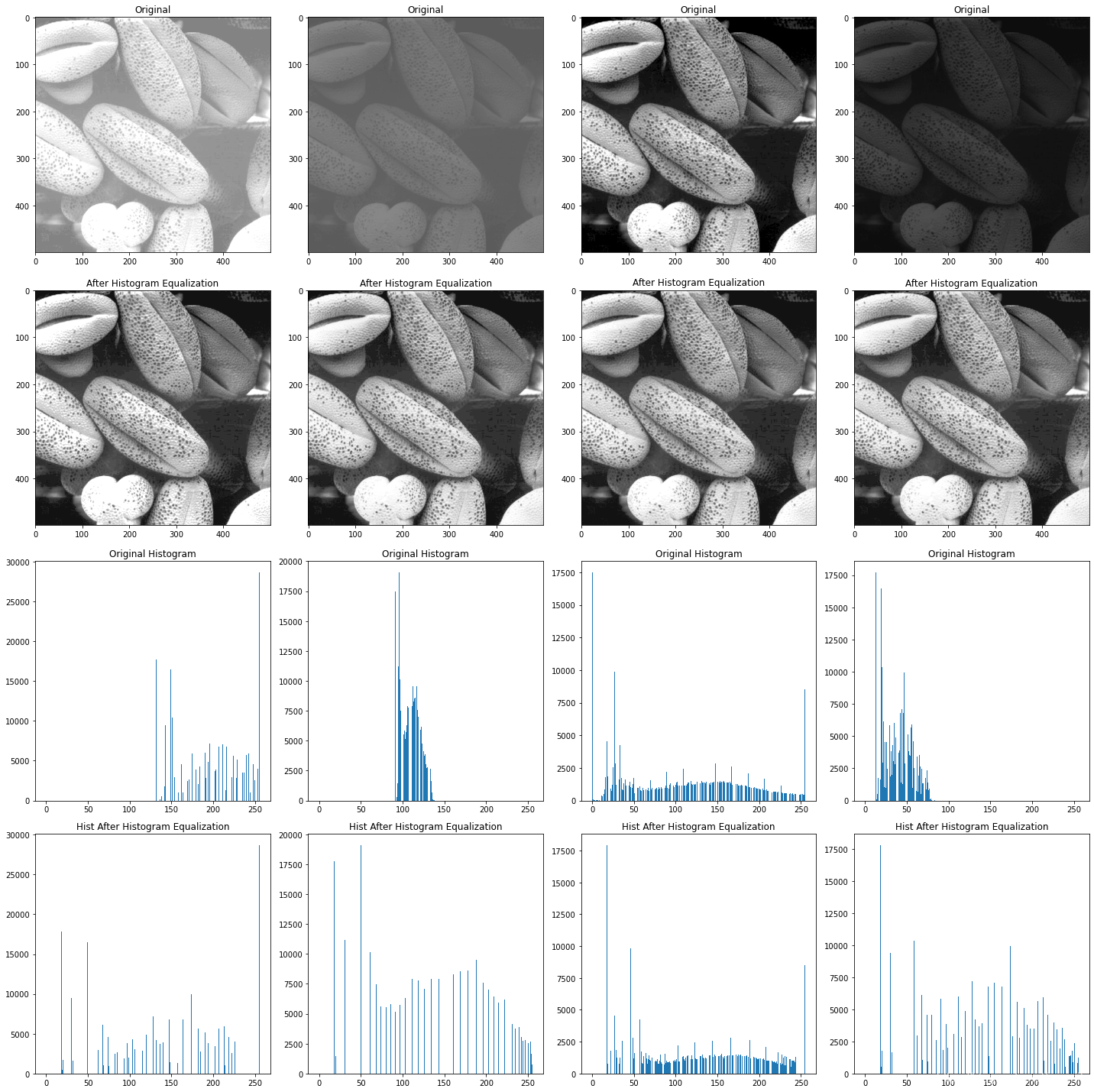
def my_calhist(img):"""histogram equalizationparam: input img: uint8[0, 255] grayscale imagereturn uint8[0, 255] grayscale image after histogram equalization"""hist, bins = my_hist(img, bins=256, normalized=True)hist_cumsum = np.round(np.cumsum(hist) * 255).astype(int)height, width = img.shape[:2]img_dst = np.zeros([height, width], np.uint8)for h in range(height):for w in range(width):img_dst[h, w] = hist_cumsum[img[h, w]] # dict 用[ ]img_dst = np.clip(img_dst, 0, 255).astype(np.uint8)return img_dst, hist_cumsum

# 直方图均衡化转换函数
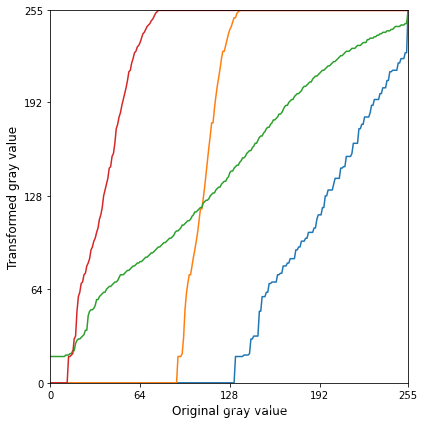
img_1st = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(1)(top_left).tif', 0)
img_2nd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(2)(2nd_from_top).tif', 0)
img_3rd = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(3)(third_from_top).tif', 0)
img_4th = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0316(4)(bottom_left).tif', 0)img_list =['img_1st', 'img_2nd', 'img_3rd', 'img_4th']fig = plt.figure(figsize=(6, 6))
for i in range(len(img_list)):# plot histogram equalization transform_, map_dict = my_calhist(eval(img_list[i]))ax1 = fig.gca()ax1.plot(map_dict)plt.xlabel('Original gray value', fontsize=12)
plt.ylabel('Transformed gray value', fontsize=12)
plt.xticks([0, 64, 128, 192, 255])
plt.yticks([0, 64, 128, 192, 255])
plt.xlim([0, 255])
plt.ylim([0, 255])
plt.tight_layout()
plt.show()