一【题目类别】

• 矩阵

二【题目难度】

• 困难

三【题目编号】

• 85.最大矩形

四【题目描述】

• 给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

五【题目示例】

• 示例 1：

  • 
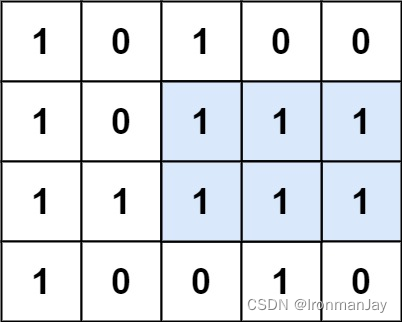
  • 输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
  • 输出：6
  • 解释：最大矩形如上图所示。

• 示例 2：

  • 输入：matrix = []
  • 输出：0

• 示例 3：

  • 输入：matrix = [[“0”]]
  • 输出：0

• 示例 4：

  • 输入：matrix = [[“1”]]
  • 输出：1

• 示例 5：

  • 输入：matrix = [[“0”,“0”]]
  • 输出：0

六【题目提示】

• $rows==matrix.length$
• $cols==matrix[0].length$
• $1<=row,cols<=200$
• $matrix[i][j]{为}^{\prime }{0}^{\prime }{或}^{\prime }{1}^{\prime }$

七【解题思路】

• 首先创建一个辅助数组left，用于记录每个位置的左边连续 ‘1’ 的个数
• 然后对于二维数组中每一个点，我们计算以这个点作为右下角的矩形的面积，我们利用“向上拓展”的方式，矩阵的宽度是“向上拓展”的过程中最短的宽度，高度通过当前位置减去遍历到的位置然后加一得到（因为数组从零开始计数）
• 然后通过比较最大值得到最大矩形的面积
• 最后返回结果即可

八【时间频度】

• 时间复杂度：$O(m^{2}n)$，$m、n$分别为传入的二维数组的行数和列数
• 空间复杂度：$O(mn)$，$m、n$分别为传入的二维数组的行数和列数

九【代码实现】

1. Java语言版

class Solution {public int maximalRectangle(char[][] matrix) {int m = matrix.length;int n = matrix[0].length;int[][] left = new int[m][n];for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '1'){left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;}}}int res = 0;for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '0'){continue;}int width = left[i][j];int area = width;for(int k = i - 1;k >= 0;k--){width = Math.min(width, left[k][j]);area = Math.max(area,(i - k + 1) * width);}res = Math.max(res, area);}}return res;}
}

2. C语言版

int maximalRectangle(char** matrix, int matrixSize, int* matrixColSize)
{int m = matrixSize;int n = matrixColSize[0];int** left = (int **)malloc(sizeof(int*) * m);for(int i = 0;i < m;i++){left[i] = (int*)calloc(n, sizeof(int));}for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '1'){left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;}}}int res = 0;for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '0'){continue;}int width = left[i][j];int area = width;for(int k = i - 1;k >= 0;k--){width = fmin(width, left[k][j]);area = fmax(area, (i - k + 1) * width);}res = fmax(res, area);}}return res;
}

3. Python语言版

class Solution:def maximalRectangle(self, matrix: List[List[str]]) -> int:m = len(matrix)n = len(matrix[0])left = [[0 for _ in range(n)] for _ in range (m)]for i in range(0, m):for j in range(0, n):if matrix[i][j] == '1':left[i][j] = (0 if j == 0 else left[i][j - 1]) + 1res = 0for i in range(0, m):for j in range(0, n):if matrix[i][j] == '0':continuewidth = left[i][j]area = widthfor k in range(i - 1, -1, -1):width = min(width, left[k][j])area = max(area, (i - k + 1) * width)res = max(res, area)return res

4. C++语言版

class Solution {
public:int maximalRectangle(vector<vector<char>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<vector<int>> left(m, vector<int>(n, 0));for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '1'){left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;}}}int res = 0;for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(matrix[i][j] == '0'){continue;}int width = left[i][j];int area = width;for(int k = i - 1;k >= 0;k--){width = fmin(width, left[k][j]);area = fmax(area, (i - k + 1) * width);}res = fmax(res, area);}}return res;}
};

十【提交结果】

1. Java语言版
   

2. C语言版
   

3. Python语言版
   

4. C++语言版