softmax函数–softmax layer
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类!
假设我们有一个数组z=(z1,z2,...zm),则其softmax函数定义如下:
也就是softmax是个函数映射,将 z=(z1,z2,...zm)映射到 (σ1,σ2,...σm).
其中, ∑σi=1.
如下图,可以更清楚地表明。

在logistic回归中,假设zi=wTix+bi是第i个类别的线性预测结果,带入softmax中就可以得到oi=σi(z)可以解释成观察得到的数据x属于类别i的概率,或者称为似然(Likehood)。
logistic regression
Logistic Regression 的目标函数是根据最大似然原则来建立的,假设数据x所对应的类别为 y,则根据x我们刚才的计算最大似然就是要最大化oy的值
通常是使用 negative log-likelihood 而不是likelihood,也就是说最小化−log(oy)的值,这两者结果在数学上是等价的。即min−log(oy)<=>max oy
后面这个操作就是 caffe 文档里说的 Multinomial Logistic Loss,具体写出来是这个样子:
从上面可以看出,计算似然损失,其实是和label一起的。这也是情理之中的,既然我们知道label是某一个,自然我们我希望对应的预测概率尽可能大一点。这就归结于上面的log损失。
softmax logistic loss
softmax logistic loss就是将softmax与上述的log损失结合到一起,只要把oy的定义展开即可。
其实label(这里指y)的作用就是指定了softmax的序号,也就是告诉是哪一些最小化。
反向传播
反向传播,要求根据loss更新weights,需要计算loss对于weight的偏导数。
我们参考了网上的一个例子,来简单介绍一下如何计算偏导。

好了,我们的重头戏来了,怎么根据求梯度,然后利用梯度下降方法更新梯度!
要使用梯度下降,肯定需要一个损失函数,这里我们使用交叉熵作为我们的损失函数,为什么使用交叉熵损失函数,不是这篇文章重点,后面有时间会单独写一下为什么要用到交叉熵函数(这里我们默认选取它作为损失函数)
交叉熵函数形式如下:

其中y代表我们的真实值,a代表我们softmax求出的值。i代表的是输出结点的标号!在上面例子,i就可以取值为4,5,6三个结点(当然我这里只是为了简单,真实应用中可能有很多结点)
现在看起来是不是感觉复杂了,居然还有累和,然后还要求导,每一个a都是softmax之后的形式!
但是实际上不是这样的,我们往往在真实中,如果只预测一个结果,那么在目标中只有一个结点的值为1,比如我认为在该状态下,我想要输出的是第四个动作(第四个结点),那么训练数据的输出就是a4 = 1,a5=0,a6=0,哎呀,这太好了,除了一个为1,其它都是0,那么所谓的求和符合,就是一个幌子,我可以去掉啦!
交叉熵函数形式如下:

这就回到了我们的softmax logistic loss,其实发现交叉熵损失与softmax logistic loss在输出只有一个类的时候等价。
参数的形式在该例子中,总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些,那么比如我要求出w41,w42,w43的偏导,就需要将Loss函数求偏导传到结点4,然后再利用链式法则继续求导即可,举个例子此时求w41的偏导为:
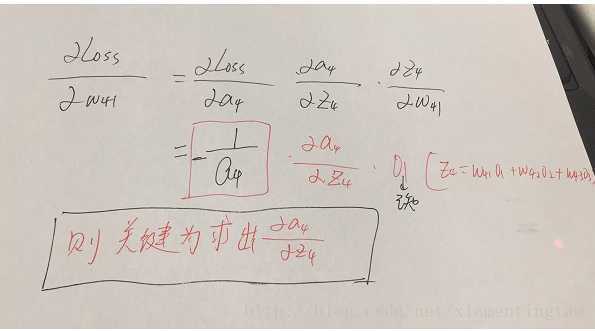
w51…..w63等参数的偏导同理可以求出,那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求,如下:
这里分为俩种情况:

j=i对应例子里就是如下图所示:
比如我选定了j为4,那么就是说我现在求导传到4结点这!



这里对应我的例子图如下,我这时对的是j不等于i,往前传:


参考文献
- Softmax vs. Softmax-Loss: Numerical Stability
- Caffe中Loss Layer原理的简单梳理
- Softmax 函数的特点和作用是什么?

)











![[C#]async和await刨根问底](http://pic.xiahunao.cn/[C#]async和await刨根问底)





