来源 | 数量经济学综合整理
转载请联系

进行回归分析,一般需要研究系数的估计值是否稳定。很多经济变量都存在结构突变问题,使用普通回归的做法就是确定结构突变点,进行分段回归。这就像我们高中学习的分段函数。但是对于大样本、面板数据如何寻找结构突变点。所以本文在此讲解面板门限回归的问题,门限回归也适用于时间序列。
门限效应,是指当一个经济参数达到特定的数值后,引起另外一个经济参数发生突然转向其它发展形式的现象(结构突变)。作为原因现象的临界值称为门限值。例如,成果和时间存在非线性关系,但是在每个阶段是线性关系。有些人将这样的模型称为门槛模型,或者门限模型。如果模型的研究对象包含多个个体多个年度,那么就是门限面板模型。
1history&Hansen常见模型如下:门槛回归模型(threshold regression,也称门限回归):

汉森(Bruce E. Hansen)在门限回归模型上做出了很多贡献。Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》,提出了时间序列门限自回归模型(TAR)的估计和检验。之后,他在门限模型上连续追踪,发表了几篇经典文章,尤其是1999年的《Threshold effects in non-dynamic panels: Estimation, testing and inference》(Hansen (1999) 首次介绍了具有个体效应的面板门限模型的计量分析方法, 该方法以残差平方和最小化为条件确定门限值, 并检验门限值的显著性, 克服了主观设定结构突变点的偏误。具体思路是:选定某一变量作为门限变量, 根据搜寻到的门限值将回归模型区分为多个区间, 每个区间的回归方程表达不同, 根据门限划分的区间将其他样本值进行归类, 回归后比较不同区间系数的变化。),2000年的《Sample splitting and threshold estimation》和2004年与他人合作的《Instrumental Variable Estimation of a Threshold Model》。
在这些文章中,Hansen介绍了包含个体固定效应的静态平衡面板数据门限回归模型,阐述了计量分析方法。方法方面,首先要通过减去时间均值方程,消除个体固定效应,然后再利用OLS(最小二乘法)进行系数估计。如果样本数量有限,那么可以使用自举法(Bootstrap)重复抽取样本,提高门限效应的显著性检验效率。在Hansen(1999)的模型中,解释变量中不能包含内生解释变量,无法扩展应用领域。Caner和Hansen在2004年解决了这个问题。他们研究了带有内生变量和一个外生门限变量的面板门限模型。与静态面板数据门限回归模型有所不同,在含有内生解释变量的面板数据门限回归模型中,需要利用简化型对内生变量进行一定的处理,然后用2SLS(两阶段最小二乘法)或者GMM(广义矩估计)对参数进行估计。
2显著性检验门槛回归模型显著性检验的目的是,检验以门檻值划分的两组样本其模型估计参数是否显著不同。
因此,不存在门槛值的零假设为:Ho:两个系数相同。同时构造LM统计量:

其中,So是在零假设下的残差平方和。由于LM统计量并不服从标准的分布。因此, Hansen(2000)提出了通过“自举法”( Bootstrap)来获得渐进分布的想法,进而得出相应的概率p值,也称为 Bootstrap P值。
这种方法的基本思想是:在解释变量和门槛值给定的前提下,模拟( Simulate)产生一组因变量序列,并使其满足N(0,e2),其中e是式(4)的残差项。每得到一个自抽样样本,就可以计算出一个模拟的エM统计量。将这一过程重复1000次。Hansen(1996)认为模拟产生的LM统计量大于式(6)的次数占总模拟次数的百分比就是“自举法”估计得到的P值。这里的Bootstrap P值类似于普通计量方法得出的相伴概率P值。例如,当 Bootstrap P值小于0.01时,表示在1 %的显著性水平下通过了LM检验,以此类推。
3置信区间
以上的检验过程为只有一个门槛值的检验过程,为了能确定是否存在两个门槛值或者是更多的门槛值,我们应当检验是否存在两个门槛值,拒绝意味着至少存在一个门槛值。我们可以假设己经估计的第一个门槛值,然后开始寻找第二个门槛值。在确定有两个门槛值后,再寻找第三个门槛值,方法都和前面的一样,直至我们不能拒绝零假设。
4门槛回归及R操作主要使用pdR安装包,在pdR安装包中主要使用ptm函数。
ptm函数是估计面板门限模型的一种通用规范。
此代码只适用于平衡面板数据。它推广了Hansen(http://www.ssc.wisc.edu/~bhansen/)的简单代码,允许多个(不止一个)依赖于系统的(ind1)变量。
为了更好地适应面板数据中阈值建模的一般需要,我们对原始代码进行了改进。bootn和trimn是3×1的向量,表示三个相应的体制的数字。这个版本修正了参数max_lag引起的一个小错误,Hansen用它来通过lag安排投资数据。
在这个包中,用户操作数据以使个人研究适合ptm(),因此省略了这个论点,以免自由度会损失N。
Author(s)
Ho Tsung-wu , College of Management, National Taiwan Normal University.
References
Hansen B. E. (1999) Threshold effects in non-dynamic panels: Estimation, testing and inference. Journal of Econometrics,93, 345-368.
语法格式为:
ptm(dep, ind1, ind2, d, bootn, trimn, qn, conf_lev, t, n)选项含义为
dep:表示因变量,即被解释变量
ind1:Independent variables: regime dependent,意思为区制变量
ind2:Independent variables:regime independent,其他不受区制变量影响的变量
d:门槛变量Threshold variable
bootn:Vector of bootstrap repetition,可以理解为stata命令里面的自举抽样次数,即表示网格搜索数量
trimn:Vector of trimmed percentage,修整比例,根据门槛个数来确定,具体请看下面案例,1 2 3个门槛时候该选项不一致,请看案例
qn:Number of quantiles to examine,门限变量分割的分割点位数,一般默认为100,
conf_lev:Confidence level,置信度水平,默认为95%
t:Length of time period,时间
n:Number of cross-section units截面个数
案例代码为,首先查看源码Stata命令里面xthreg所对应的数据代码。
例如:
xthreg需要stata13及以上版本
语法格式为:
xthreg depvar [indepvars] [if] [in], rx(varlist) qx(varname) [thnum(#) grid(#) trim(numlist) bs(numlist) thlevel(#) gen(newvarname) noreg nobslog thgiven options]
depvar被解释变量,indepvars 解释变量,qx(varname) is the threshold variable,门限变量,thnum(#) is the number of thresholds,在stata13.0中门槛值是必要项目,需要等于大于1,小于等于3,默认值为1,也就是至少存在三个门槛值。
门槛回归的案例
use hansen1999
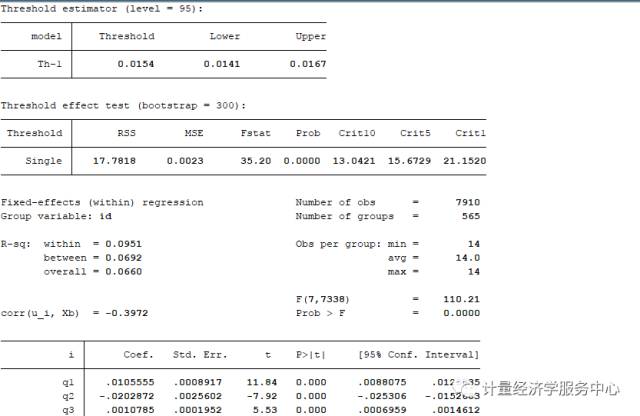
Estimate a single-threshold model
xthreg i q1 q2 q3 d1 qd1, rx(c1) qx(d1) thnum(1) trim(0.01) grid(400) bs(300)
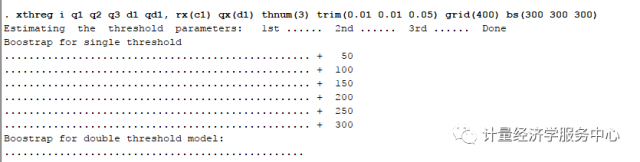
Estimate a triple-threshold model given the estimated result above
xthreg i q1 q2 q3 d1 qd1, rx(c1) qx(d1) thnum(3) trim(0.01 0.01 0.05) grid(400) bs(300 300 300)
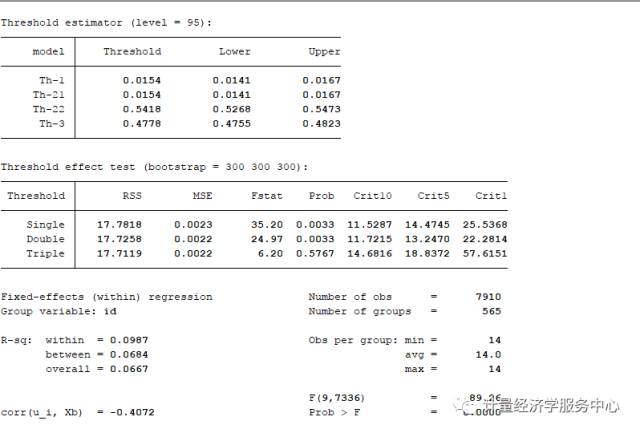
输出结果包括四个部分。第一部分输出门限估计值和自举法的结果。第二部分列表输出门限值及置信区间,Th-1代表单一门限估计值,Th-21 和Th-22代表双门限回归的两个估计值,有时Th-21和Th-1相同。第三部分列出了门限检验,包括RSS、MSE、F统计量及概率值,以及10%、5%、1%的置信水平。第四部分是固定效应回归结果。
那么通过这个例子上面对应的位置就可以很好的理解R操作门槛回归了!
4.1单门槛回归及R操作1、单门槛回归命令代码
# R统计分析与应用# 经济金融数据分析及R应用# # 计量经济学服务中心# 2018年1月setwd("C:\\Users\\admin\\Desktop")library(readstata13) library(pdR)# 导入数据(计量经济学服务中心)hansen "hansen1999.dta")然后进行各个变量设置:
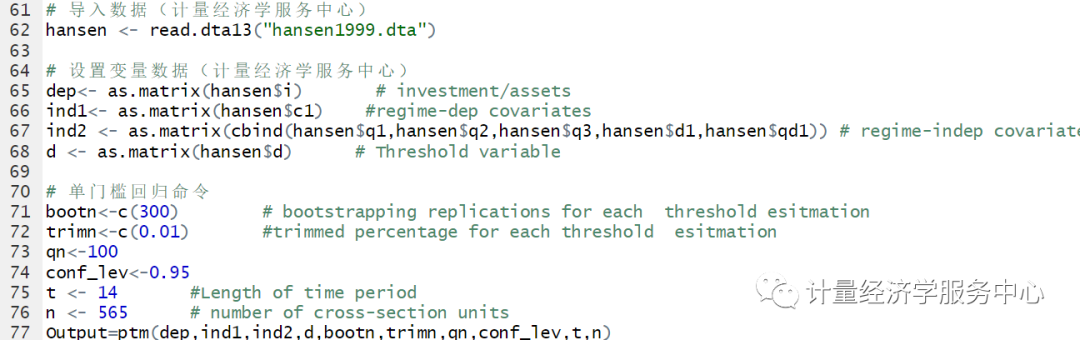
结果为:
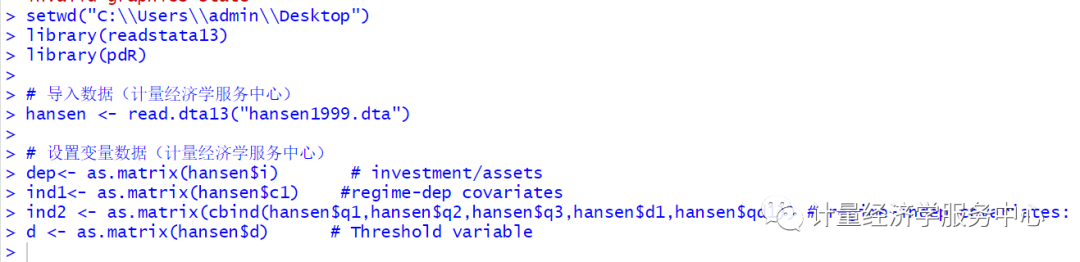
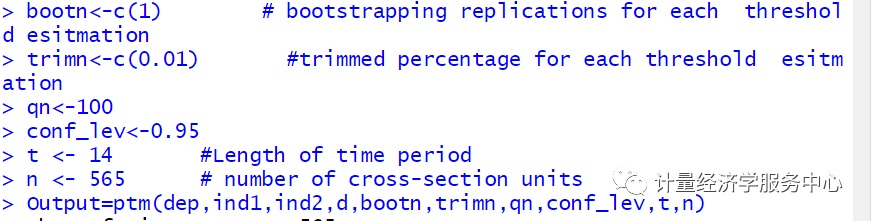
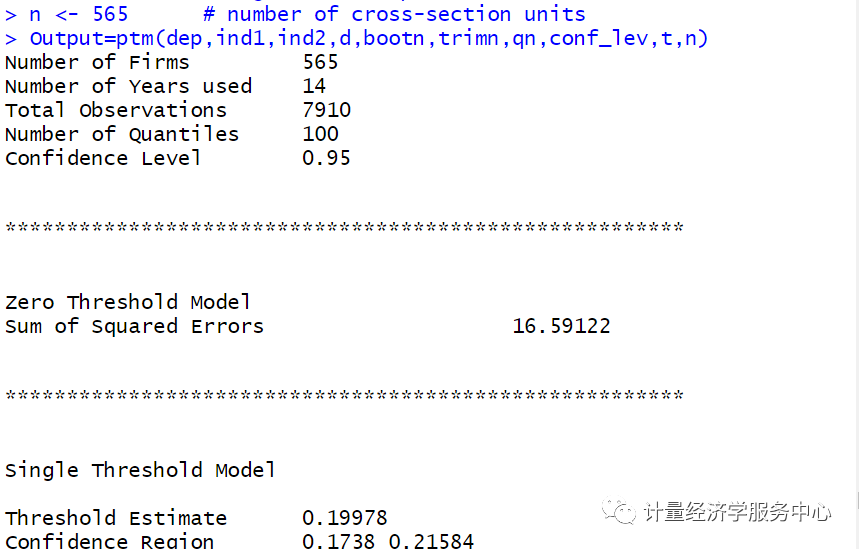
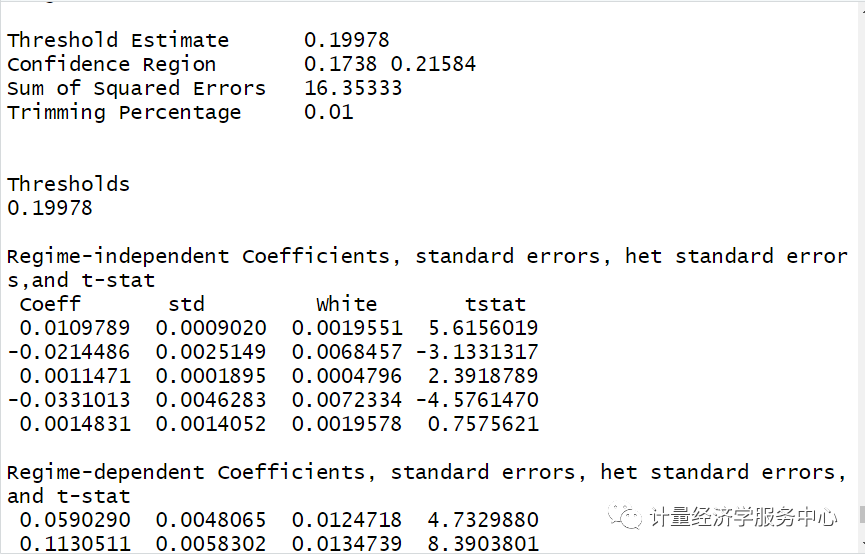


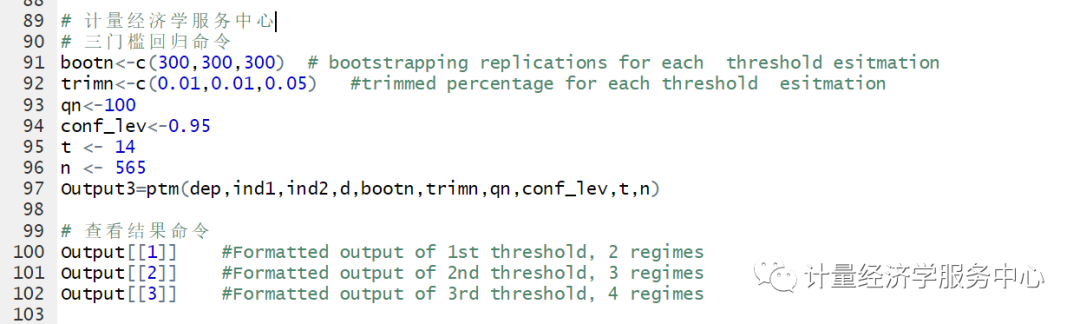
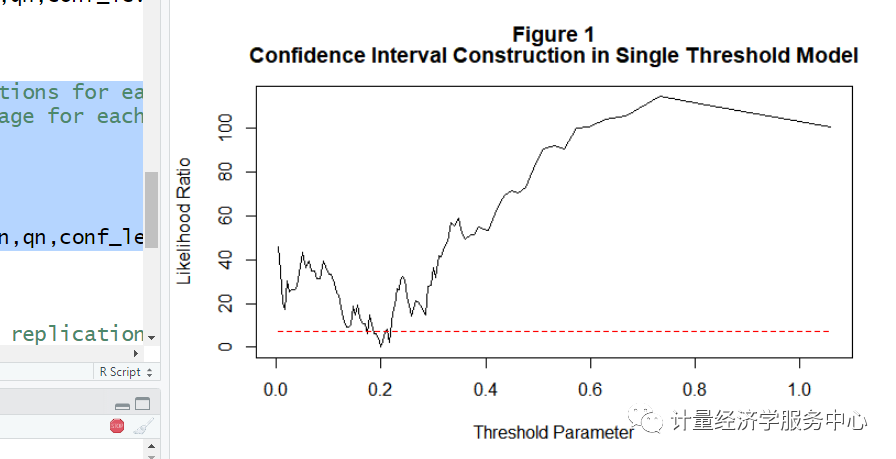
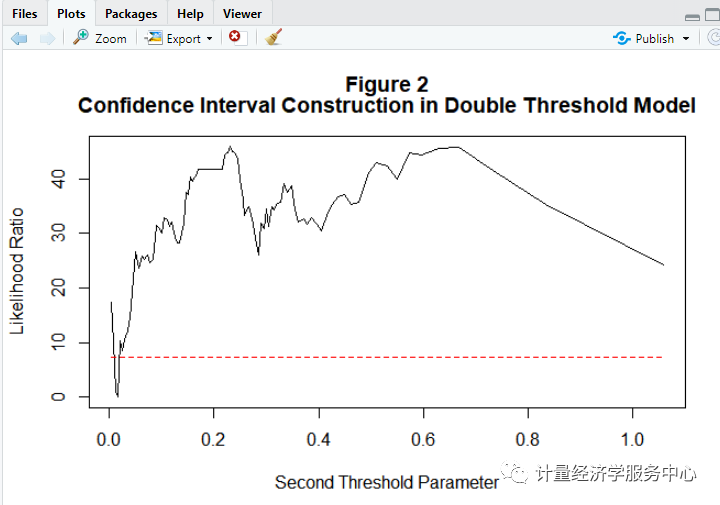
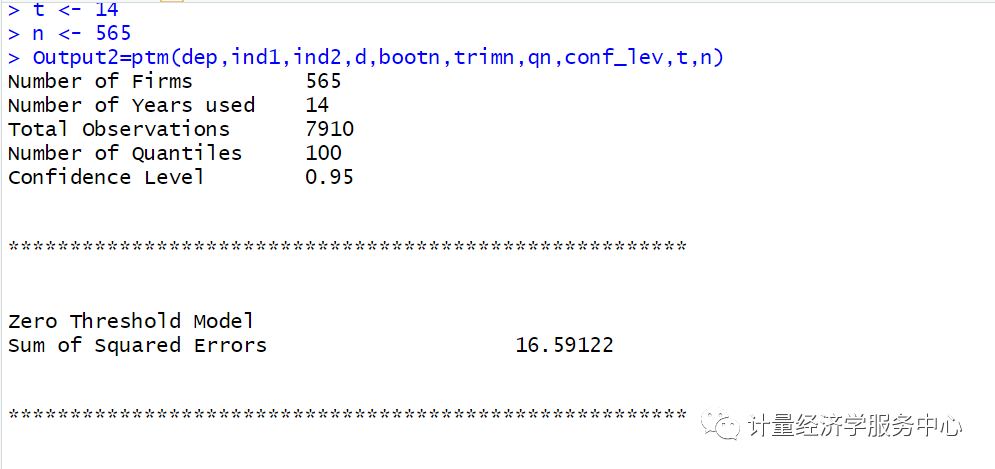
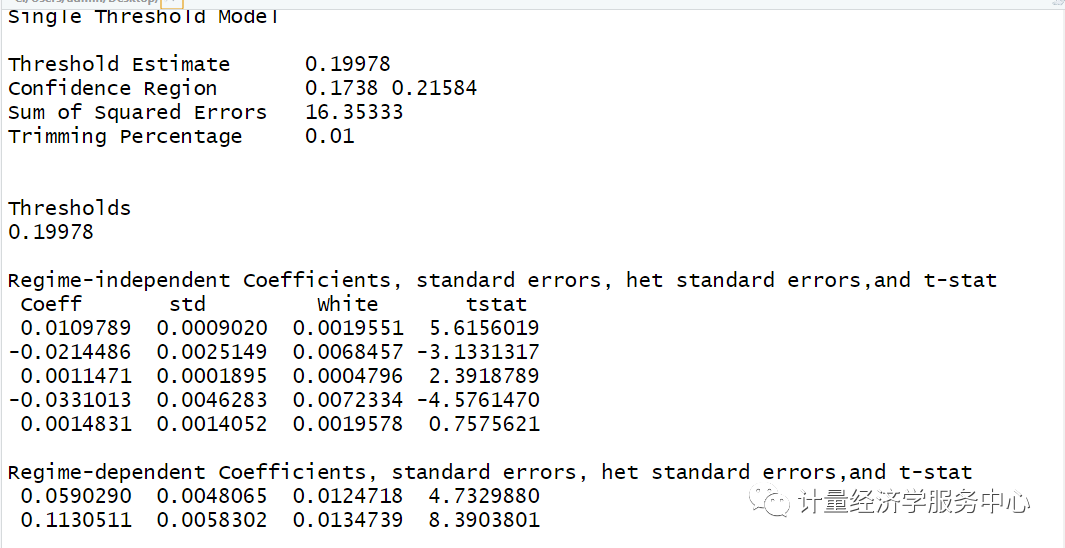
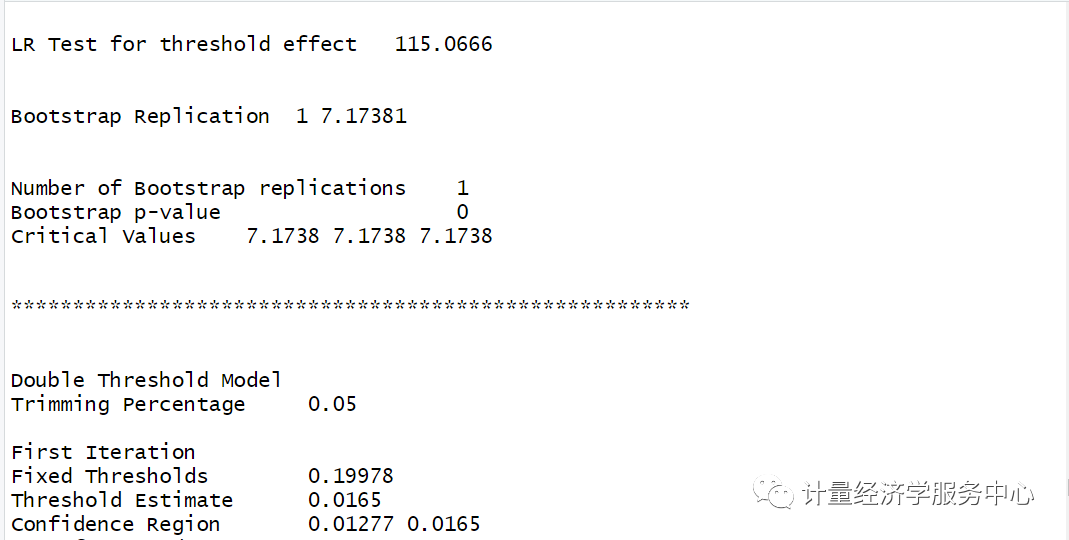

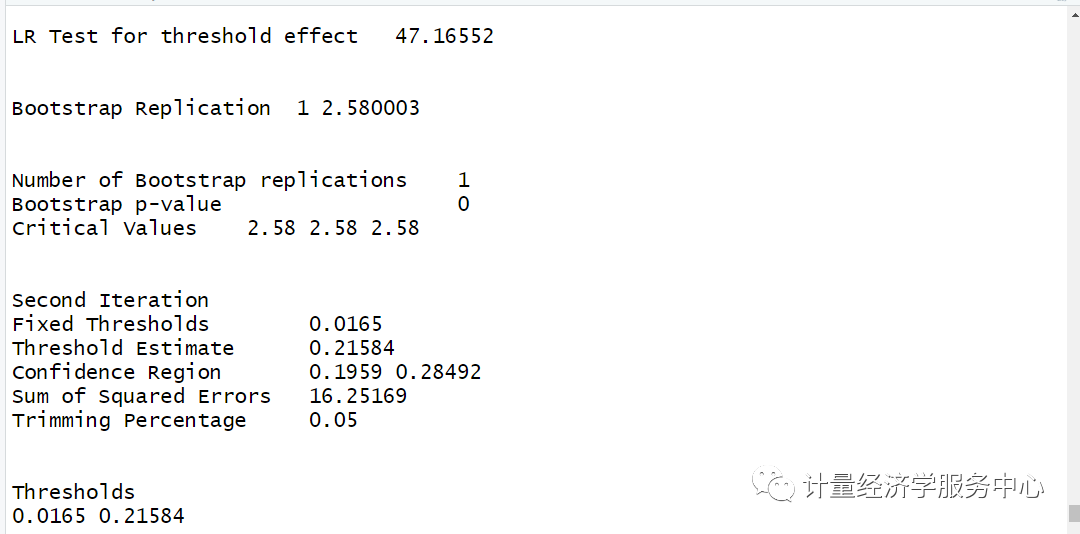
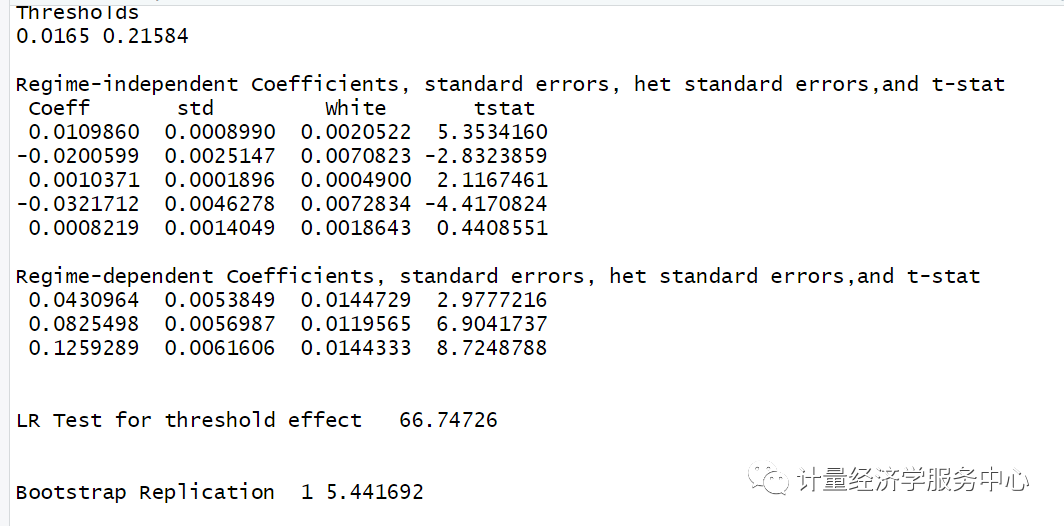
注意:上述展现的是双重门槛的结果,然后自抽样次数修改为1出来的结果,这样保证了软件运行出来的速度。
另外上述结果与Stata出来结果有细小的差别!
![【数论】[CF258C]Little elephant and LCM](http://pic.xiahunao.cn/【数论】[CF258C]Little elephant and LCM)




)

![BZOJ1050 [HAOI2006]旅行](http://pic.xiahunao.cn/BZOJ1050 [HAOI2006]旅行)











