C4.5

C4.5是机器学习算法中的另一个分类决策树算法，它是基于ID3算法进行改进后的一种重要算法，相比于ID3算法，改进有如下几个要点：

• 用信息增益率来选择属性。ID3选择属性用的是子树的信息增益，这里可以用很多方法来定义信息，ID3使用的是熵（entropy， 熵是一种不纯度度量准则），也就是熵的变化值，而C4.5用的是信息增益率。
• 在决策树构造过程中进行剪枝，因为某些具有很少元素的结点可能会使构造的决策树过适应（Overfitting），如果不考虑这些结点可能会更好。
• 对非离散数据也能处理。
• 能够对不完整数据进行处理。

首先，说明一下如何计算信息增益率。
熟悉了ID3算法后，已经知道如何计算信息增益，计算公式如下所示（来自Wikipedia）：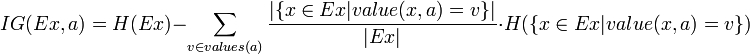

或者，用另一个更加直观容易理解的公式计算：

• 按照类标签对训练数据集D的属性集A进行划分，得到信息熵：

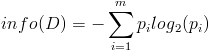
• 按照属性集A中每个属性进行划分，得到一组信息熵：

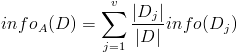
• 计算信息增益

然后计算信息增益，即前者对后者做差，得到属性集合A一组信息增益：

这样，信息增益就计算出来了。

• 计算信息增益率

下面看，计算信息增益率的公式，如下所示（来自Wikipedia）：

其中，IG表示信息增益，按照前面我们描述的过程来计算。而IV是我们现在需要计算的，它是一个用来考虑分裂信息的度量，分裂信息用来衡量属性分 裂数据的广度和均匀程序，计算公式如下所示（来自Wikipedia）：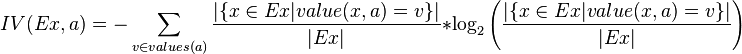

简化一下，看下面这个公式更加直观：

其中，V表示属性集合A中的一个属性的全部取值。

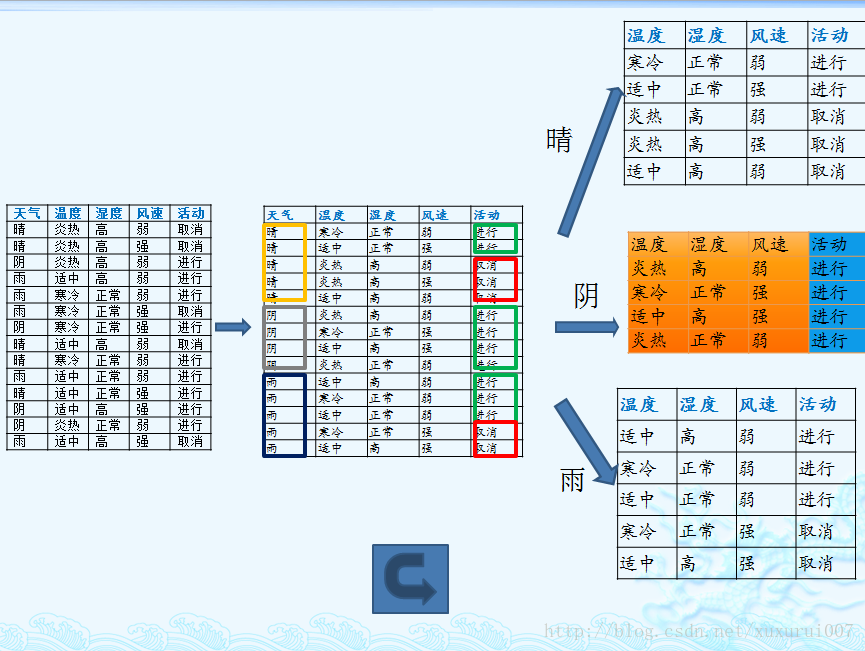
我们以一个很典型被引用过多次的训练数据集D为例，来说明C4.5算法如何计算信息增益并选择决策结点。

上面的训练集有4个属性，即属性集合A={OUTLOOK, TEMPERATURE, HUMIDITY, WINDY}；而类标签有2个，即类标签集合C={Yes, No}，分别表示适合户外运动和不适合户外运动，其实是一个二分类问题。
我们已经计算过信息增益，这里直接列出来，如下所示：
数据集D包含14个训练样本，其中属于类别“Yes”的有9个，属于类别“No”的有5个，则计算其信息熵：

1	Info(D) = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940

下面对属性集中每个属性分别计算信息熵，如下所示：

1	Info(OUTLOOK) = 5/14 * [- 2/5 * log2(2/5) – 3/5 * log2(3/5)] + 4/14 * [ - 4/4 * log2(4/4) - 0/4 * log2(0/4)] + 5/14 * [ - 3/5 * log2(3/5) – 2/5 * log2(2/5)] = 0.694

2 Info(TEMPERATURE) = 4/14 * [- 2/4 * log2(2/4) – 2/4 * log2(2/4)] + 6/14 * [ - 4/6 * log2(4/6) - 2/6 * log2(2/6)] + 4/14 * [ - 3/4 * log2(3/4) – 1/4 * log2(1/4)] = 0.911

3	Info(HUMIDITY) = 7/14 * [- 3/7 * log2(3/7) – 4/7 * log2(4/7)] + 7/14 * [ - 6/7 * log2(6/7) - 1/7 * log2(1/7)] = 0.789

4 Info(WINDY) = 6/14 * [- 3/6 * log2(3/6) – 3/6 * log2(3/6)] + 8/14 * [ - 6/8 * log2(6/8) - 2/8 * log2(2/8)] = 0.892

根据上面的数据，我们可以计算选择第一个根结点所依赖的信息增益值，计算如下所示：

1	Gain(OUTLOOK) = Info(D) - Info(OUTLOOK) = 0.940 - 0.694 = 0.246

2 Gain(TEMPERATURE) = Info(D) - Info(TEMPERATURE) = 0.940 - 0.911 = 0.029

3	Gain(HUMIDITY) = Info(D) - Info(HUMIDITY) = 0.940 - 0.789 = 0.151

4 Gain(WINDY) = Info(D) - Info(WINDY) = 0.940 - 0.892 = 0.048

接下来，我们计算分裂信息度量H(V)：

• OUTLOOK属性

属性OUTLOOK有3个取值，其中Sunny有5个样本、Rainy有5个样本、Overcast有4个样本，则

1	H(OUTLOOK) = - 5/14 * log2(5/14) - 5/14 * log2(5/14) - 4/14 * log2(4/14) = 1.577406282852345

• TEMPERATURE属性

属性TEMPERATURE有3个取值，其中Hot有4个样本、Mild有6个样本、Cool有4个样本，则

1	H(TEMPERATURE) = - 4/14 * log2(4/14) - 6/14 * log2(6/14) - 4/14 * log2(4/14) = 1.5566567074628228

• HUMIDITY属性

属性HUMIDITY有2个取值，其中Normal有7个样本、High有7个样本，则

1	H(HUMIDITY) = - 7/14 * log2(7/14) - 7/14 * log2(7/14) = 1.0

• WINDY属性

属性WINDY有2个取值，其中True有6个样本、False有8个样本，则

1	H(WINDY) = - 6/14 * log2(6/14) - 8/14 * log2(8/14) = 0.9852281360342516

根据上面计算结果，我们可以计算信息增益率，如下所示：

1	IGR(OUTLOOK) = Info(OUTLOOK) / H(OUTLOOK) = 0.246/1.577406282852345 = 0.15595221261270145

2 IGR(TEMPERATURE) = Info(TEMPERATURE) / H(TEMPERATURE) = 0.029 / 1.5566567074628228 = 0.018629669509642094

3	IGR(HUMIDITY) = Info(HUMIDITY) / H(HUMIDITY) = 0.151/1.0 = 0.151

4 IGR(WINDY) = Info(WINDY) / H(WINDY) = 0.048/0.9852281360342516 = 0.048719680492692784

根据计算得到的信息增益率进行选择属性集中的属性作为决策树结点，对该结点进行分裂。

C4.5算法的优点是：产生的分类规则易于理解，准确率较高。
C4.5算法的缺点是：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。

参考链接

• http://blog.sina.com.cn/s/blog_68ffc7a40100urn3.html
• http://en.wikipedia.org/wiki/Information_gain_ratio
• http://blog.sina.com.cn/s/blog_54c5622701016h4j.html
• http://en.wikipedia.org/wiki/Information_gain_ratio
• http://baike.baidu.com/view/8775136.htm
• http://www.cnblogs.com/zhangchaoyang/articles/2842490.html
• http://private.codecogs.com/latex/eqneditor.php

quote:http://shiyanjun.cn/archives/428.html

C