目录
一、问题描述(兵王问题)
二、步骤
1、获得数据
2、样本划分(训练样本和测试样本)
3、训练样本得到SVM模型
1)数据处理
2)训练样本和测试样本归一化
3)选择核函数和调参
4)明确任务
5)训练方法——交叉验证
6)参数的设置
3、获得训练后的参数
>>>问题1:为什么要获得这些参数呢?
4、测试结果分析
1)二元分类一般要将测试结果分为四种情况(TP\FN\TN\FP)
2)测试样本测试结果
5、对模型系统进行评价——ROC曲线
1)测试数据的流程:
>>>问题2:若正样本数不够多该怎么办?
2)提升系统性能的办法
3)ROC曲线
>>>问题3:怎么通过ROC曲线去评价一个系统的优劣?
4)系统性能评价指标1:有一个指标就是当FP接近0的时候,TP的大小
5)系统性能评价指标2:曲线所包含的面积(AUC)
6) 系统性能评价指标3:等容错率(EER)
一、问题描述(兵王问题)
国际象棋中,一方一个王一个兵,另一方一个王,用SVM来解决是和局还是将死的结果
二、步骤
1、获得数据
这里使用的是早期别人用过的数据集
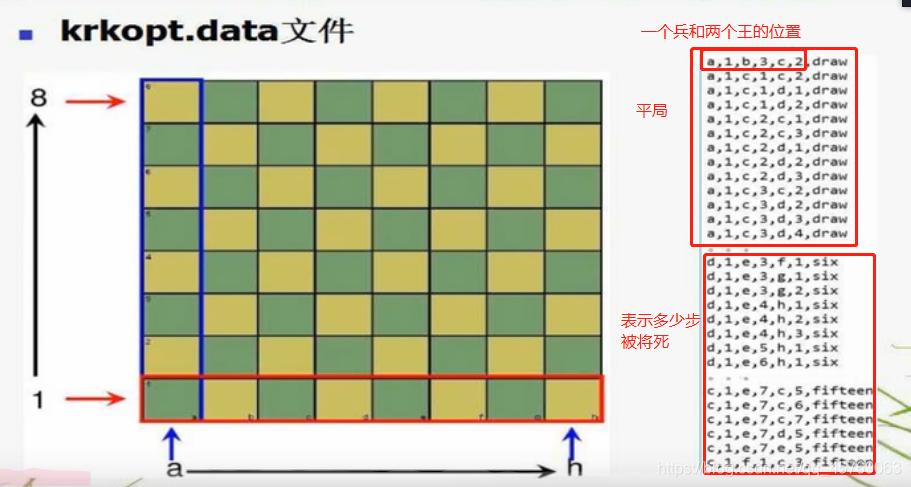
2、样本划分(训练样本和测试样本)

3、训练样本得到SVM模型
用下面的工具包对从总样本划分出来的训练样本进行训练
 1)数据处理
1)数据处理
因为电脑只认得数字所以,将a,b,c,d...用数字表示,如a=1,b=2,如此类推,标签也是:draw = -1,one-fifteen = 1(-1表示和局,1表示将死)
2)训练样本和测试样本归一化

3)选择核函数和调参
当不知道选择什么核函数的时候,我们就选择高斯核
这里的参数有两个,一个是C,一个是gamma,如何确定这两个参数?通过对偶问题中的目标函数来对两个参数在他们的取值范围内按照一定的步长逐一进行测试,取最优作为两个参数的最终取值,如下C和gamma的组合有21x19,步长为2

4)明确任务
已知——5000个训练样本(包含样本数据和每个数据对应的标签)
未知、任务——C、gamma参数,通过训练样本训练出SVM模型
5)训练方法——交叉验证
将5000个样本随机均分为5组(5——fold),5组名字分别为a,b,c,d,e,每次拿4组数据作为训练模型,1组用于测试,每组数据进行轮换测试,最后模型的辨识率取五次测试辨识率的均值

组数越多,越精确,但是训练时间多,因此需要进行权衡
这里涉及到了两个循环,一个循环是遍历所有的C和gamma,一个循环是将训练样本分成5组轮换进行训练测试
6)参数的设置
3、获得训练后的参数

>>>问题1:为什么要获得这些参数呢?
答:C和gamma确定了对偶问题模型
支持向量的个数可以通过经验来判断训练的好坏,若支持向量过多则没有训练好
通过b和α我们可以对测试样本进行分类,其中α是通过对偶问题求解所得

4、测试结果分析
5000样本用于了训练,那么剩下的样本则用于测试,通常训练的样本不能拿来测试,因为模型本来就是通过训练样本进行创建的,我们的目的是用训练得到的模型对其他样本进行分类,考察的是模型的学习能力,类似于学习过程中的知识迁移
1)二元分类一般要将测试结果分为四种情况(TP\FN\TN\FP)
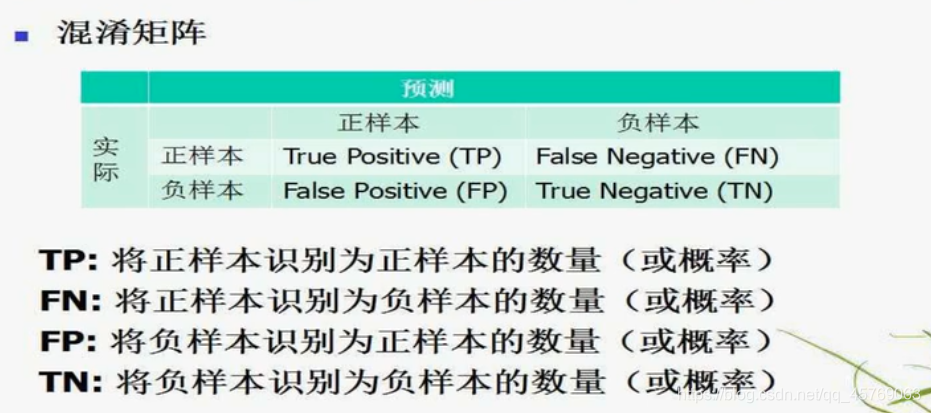
2)测试样本测试结果
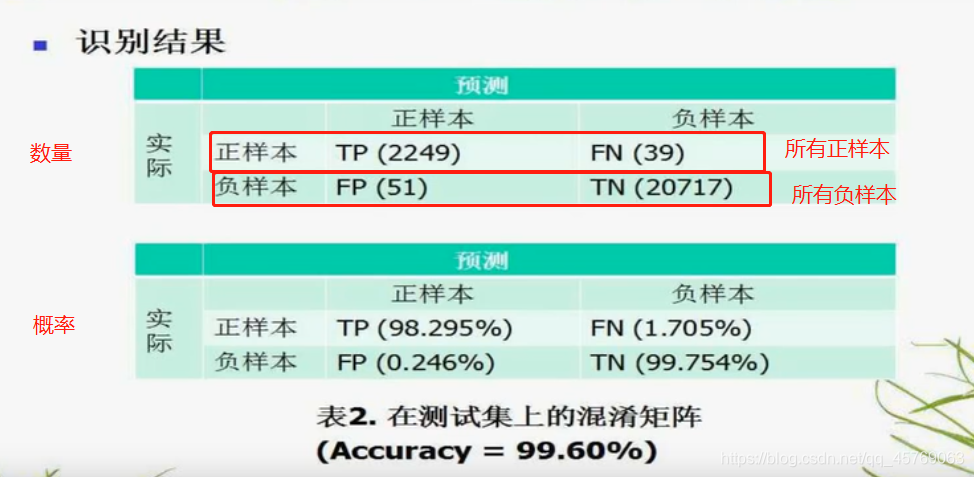
识别率一般不用来作为系统优劣的判断依据,因为不够准确,一般是通过ROC来进行判断
5、对模型系统进行评价——ROC曲线
1)测试数据的流程:

>>>问题2:若正样本数不够多该怎么办?
答:将阈值调小,就会有更多被错误识别为负样本的正样本被正确地识别为正样本,即TP增大,同时NP也会增大,这样的话系统的性能也会得到提升

2)提升系统性能的办法
方法1:在模型还没有确定的情况下,通过寻找一组更好的α和b来创建模型;
方法2:在模型确定的情况下,即α和b一定的情况下,我们可以通过适当地调小阈值来达到系统性能提升的效果
3)ROC曲线
理论依据:

曲线绘制 :根据上图的①②③关系进行绘制TP-FP曲线
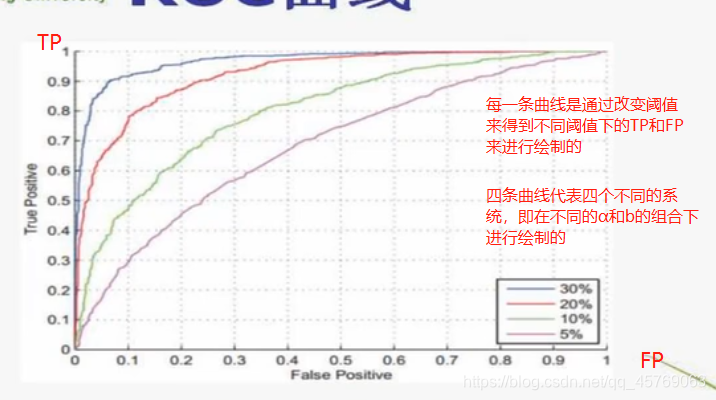
>>>问题3:怎么通过ROC曲线去评价一个系统的优劣?
答:在回答这个问题之前,我们得清楚TP和FP,TP指的是将正样本正确的识别为正样本,FP是将负样本错误地识别为正样本。
4)系统性能评价指标1:有一个指标就是当FP接近0的时候,TP的大小
指标1:有一个指标就是当FP接近0的时候,TP的大小可以用来评价一个系统的优劣,越大越好,因为识别率高。但是大多数情况下不能只看这一项指标,还要看一下总的走势,如下图所示:
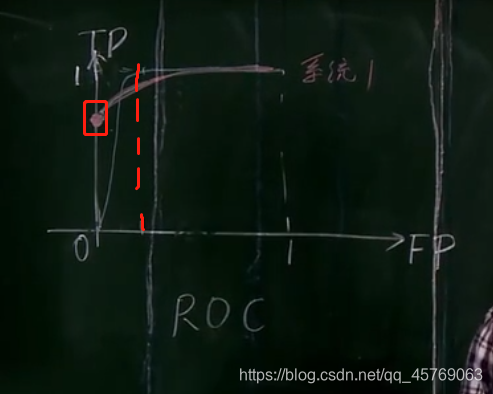
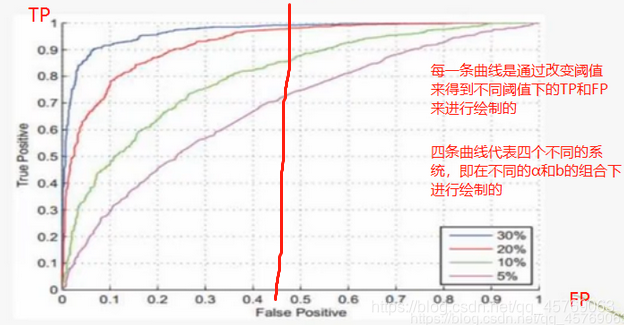
在FP=0的时候,红色线系统TP很高,但是蓝线TP=0,而到了后面,相同的FP下,蓝色线的TP大于红色线的TP,这样的两个系统无法直接判断出哪个系统更优。
但是在兵王问题中的ROC曲线,对任意相同的FP下,蓝色线所代表的系统的TP都要大于等于其他系统,因此蓝色线所代表的系统肯定在这四个系统中是最优的!
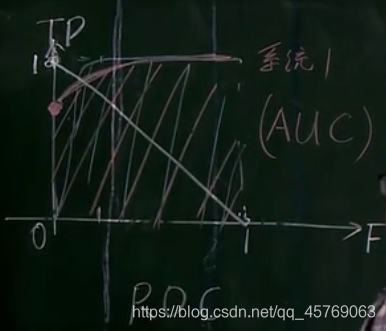
5)系统性能评价指标2:曲线所包含的面积(AUC)
面积越大,系统越优
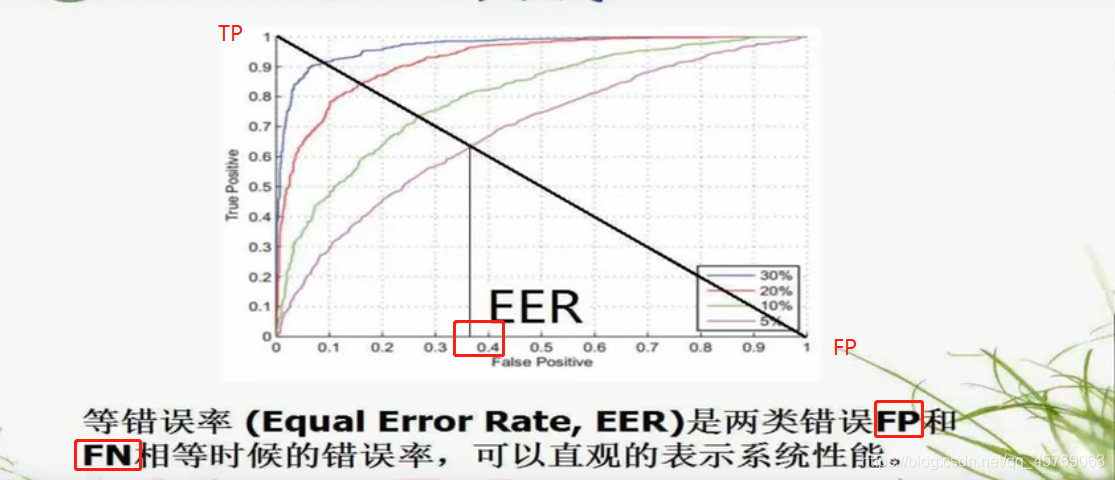
6)系统性能评价指标3:等容错率(EER)
EER越小,系统性能越好





)




)


)

)


)
