目录

一、标准化和归一化的目的

1、标准化

2、归一化

二、标准化和归一化常用的理论公式

1、归一化

2、标准化

三、python实现SVM样本数据标准化和归一化

1、标准化

2、归一化

---

本文源代码：《机器学习——支持向量机SVM之python实现简单实例一》

一、标准化和归一化的目的

1、标准化（scale）

将每个数据特征数据均值变为0，标准差变为1

标准化的目的是为了下一步数据的处理提供方便，而进行数据缩放等变化

 

  数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

    目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

2、归一化（normalization）

1 把数变为（0，1）或者（-1，1）之间的小数

归一化的目的是为了消除不同数据之间的量纲，方便数据比较和共同处理
        主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速，应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
        归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。 比如，复数阻抗可以归一化书写：Z = R + jωL = R(1 + jωL/R) ，复数部分变成了纯数量了，没有量纲。
另外，微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

实际上是如下图所示的决策边界比较合理，这就需要通过标准化来进行实现，支持向量4个

 

二、标准化和归一化常用的理论公式

具体怎么计算一个矩阵的均值和方差网上很多不再赘述

1、归一化

2、标准化

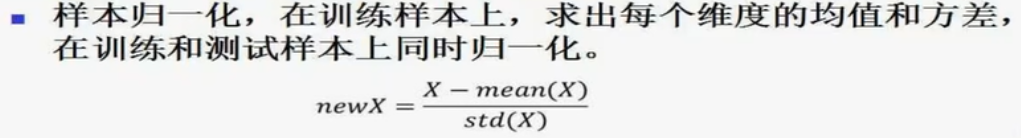
三、python实现SVM样本数据标准化和归一化

建议自己按照公式进行编程

1、标准化

 

标准化的公式很简单，步骤如下

1.求出各变量（指标）的算术平均值（数学期望）xi和标准差si ；
2.进行标准化处理：
zij=（xij－xi）/si
其中：zij为标准化后的变量值；xij为实际变量值。
3.将逆指标前的正负号对调。
标准化后的变量值围绕0上下波动，大于0说明高于平均水平，小于0说明低于平均水平。

 

常用

from sklearn import preprocessing
import numpy as np
......
x_scaled = preprocessing.scale(x)#x是要进行标准化的样本数据
......

除了用scale函数，还可以用以下几种方法对数据进行标准化

#样本数据归一化，标准化
from sklearn.preprocessing import StandardScaler
standardscaler = StandardScaler()
#对数组x遍历，对每一个样本进行标准化
standardscaler.fit(x)
#返回类StandardScaler()<class'sklearn.preprocessing._data.StandardScaler'>
x_standard = standardscaler.transform(x)#返回标准化后的样本集

def z_score(x, axis):x = np.array(x).astype(float)xr = np.rollaxis(x, axis=axis)xr -= np.mean(x, axis=axis)xr /= np.std(x, axis=axis)# print(x)return x

def standardize(x):return (x - np.mean(x))/(np.std(x))

 

2、归一化

def normalize(x):return (x - np.min(x))/(np.max(x) - np.min(x))