写给自己看的学习记录：

光具有波粒二象性，由此衍生出了几何光学与衍射光学。在光学设计软件中，最常用的判断标准是查看点列图的RMS半径以及MTF图的曲线，这两者分别代表了两种传播性质的评价方式。

在刚接触光学设计时，我误认为评价标准是，将RMS半径优化到小于像元尺寸的一半即可。认为点列图好了，MTF肯定也好了，其实这是不对的，忽视了艾里斑是最小光斑的衍射理论。

后来才了解到，当点列图小于艾里斑时，RMS半径便不再可靠。用zemax软件优化过程中，主要就是衍射与几何相互对抗的过程，当RMS半径值远大于艾里斑半径时，主要看点列图；当点列图满足要求时，尽量把MTF曲线往衍射极限上优化。

艾里斑半径R=1.22λF，由于λ是设计要求，那么F的选取就很重要，艾里斑过大或者过小都会带来问题，一般来说，让艾里斑半径等于所选探测器的像元尺寸。

具体原因在

薇洛的打火机/衍射极限、MTF与相机分辨率(1)这篇博客里有很详细的介绍。

大致如下：

在空间域中，成像系统的光斑是理想图像与点扩散函数h(t)卷积的结果，而调制传递函数MTF就是系统点扩散函数h(t)经过Fourier变换的结果。

MTF是一个频域的概念，代表不同频率成分对比度的衰减，在光学评价方法中，它的单位是lp/mm，即每毫米/线对，代表每mm范围内，有几个明暗相间的正弦条纹。测试一个光学系统的MTF，就是测试对不同疏密(lp/mm为单位)的条纹的对比度衰减。（lp/mm通常是指像平面上的线对数。）

根据Shannon采样定理，对于频率为f 的信号，我们至少要用2f的频率来采样，才能把它恢复出来。从前面的叙述，我们知道，空间频率一般是用探测器上每毫米线对数来表示的，我们至少需要两个像素来采样它，即两个像素尺寸对应一个线对宽度。这也就是光学设计中奎奈斯特截止频率计算公式的由来，即：

截止频率=1/（2*像元尺寸）

那么回到最初的问题，艾里斑多大才与我们的像元尺寸相匹配，这决定了我们光学设计中F数的选择。

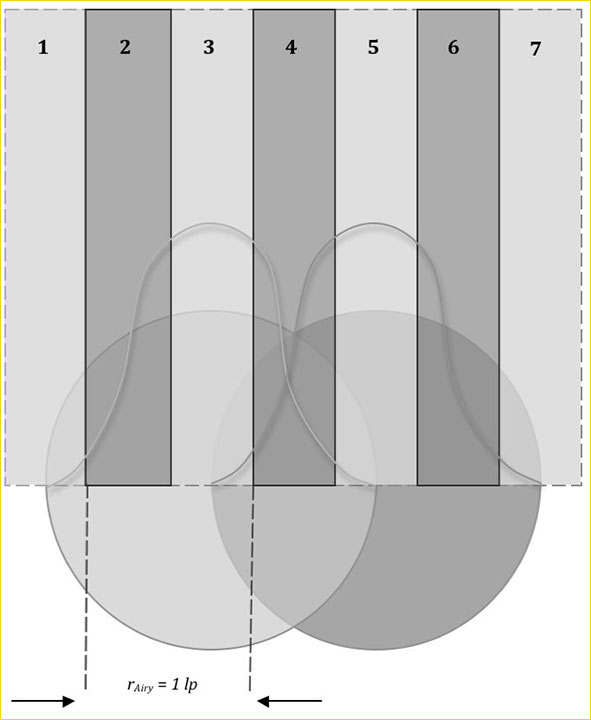
根据瑞利判据，当两个相邻的艾里斑距离为其半径时，这两个艾里斑勉强能够分辨出来。

即一个线对宽度等于艾里斑的半径，在这个频率往上，系统是衍射受限的。哪怕没有任何像差，MTF都很差，细节几乎不可分辨。

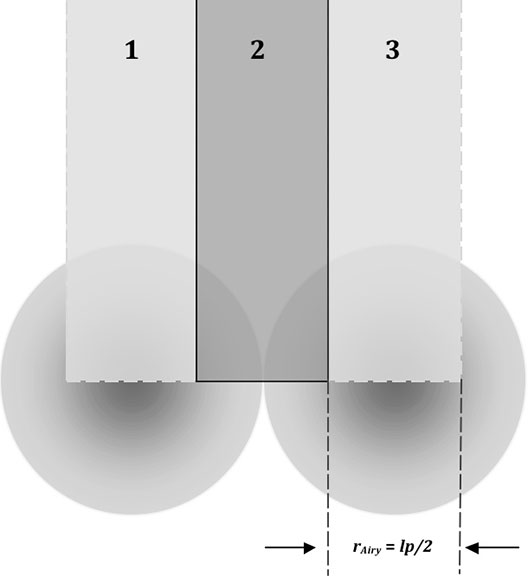
即艾里斑直径最大不能超过两个像元尺寸，否则该系统将无意义。

但是在设计中，没必要做的这么极限，另外还要考虑公差对像质的影响。

所以，一般取线对宽度等于艾里斑的直径，即一个像元尺寸等于艾里斑的半径，此时截止频率处衍射极限的MTF值约为0.5，是可以接受的。

 当然艾里斑可以更小，这样截止频率处的MTF值会更高，但是F数太大在光学设计中是件很头疼的事，各种像差带来的影响也很难使MTF接近衍射极限。

毕竟光学设计本身就是一件不断取舍的工作。

所以我们在设计中，常取F数，使得艾里斑半径等于像元尺寸大小即可。

注1：在红外设计中，将点列图优化到艾里斑内并将MTF曲线优化到接近衍射极限即可，不必太关注RMS半径值。

注2：在需求中，F数是有要求的，比如红外常要做到F1.0，反过来即可，即挑选合适的探测器。如果探测器也选定，且像元尺寸很小，那只能BIN了，牺牲分辨率。

注3：原文链接：https://blog.csdn.net/glorydream2015/article/details/44966369

（原文作者的一个例子，懒得打字，直接引用）

对于一个F数为2.8的镜头，假设我们用555nm的黄绿光来成像，像素大小做到多少合适呢？我们取线对宽度等于艾里斑的直径大小作为依据，此时只考虑衍射的话，MTF约有0.5，也还算可以了。一个线对对应两个像素，那么一个像素大小就相当于艾里斑的半径，也就是1.22λF，算出来约为1.9微米。如果固定传感器大小的话，那么它的像素数就是有上限的。到达一个限度，再增加像素数，就会导致像素小于1.9微米，再增加的像素已经提供不了新的信息了。

（批注：即艾里斑半径大于一个像素，像素和像素之间是模糊的，如果BIN的话，其实还是分辨率变少，所以现在市场上的超高像素相机或者手机实在是噱头，以致于只能宣传BIN的好处。）