OCV(on-chip variation)是指在同一个芯片上, 由于制造工艺和环境等原因导致芯片上各部分特征不能完全一样,从而造成偏差,对时序分析造成影响。这些偏差对互联线和cell的延时都是有影响的。
由于OCV对延时有影响,那么我们在进行时序分析时需要将这些OCV效应考虑进来。在STA中,通过对不同的时序路径添加derate系数,来完成对OCV的建模,将OCV效应纳入分析。
我们以下图电路为例进行说明:
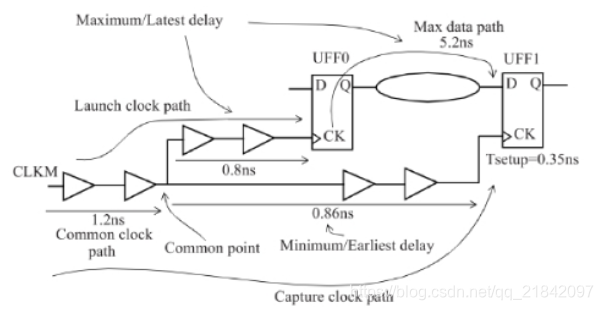
进行setup check时,最差的情况为:launch clock path 和data path由于OCV的原因,延迟增加到最大;于此同时,capture clock path 由于OCV的原因,延迟减小到最小。此时,对建立时间的检查最为严苛。
如过我们不考虑OCV的影响,进行setup check,则情况如下:
arrival time = 1.2+0.8+5.2=7.2ns
required time = 1.2+0.86-0.35+clock_period=1.71+clock_period
那么由于required time-arrival time>=0则clock_period>=5.49,即最小时钟周期为5.49ns。
接下来我们将OCV纳入考虑,为路径和cell设置不同的derate系数。
我们可以通过set_timing_derate来设置derate系数
set_timing_derate -early 0.9 set_timing_derate -late 0.9 set_timing_derate -cell_delay -late 0.9 set_timing_derate -net_delay -late 0.9长路径延时如setup check 中的launch clock path和data path,hold check中的capture clock path可以使用-late选项来设置
短路径延时如setup check 中的capture clock path,hold check中的launch clock path和data path可以使用-early选项来设置
使用-net_delay和-cell_delay来设置线网和cell的延时
为launch clock path和max data path增加系数1.2,为UFF1增加系数1.1,为capture clock path 增加系数0.9,这样,我们再看看setup check:
arrival time = (1.2+0.8+5.2)*1.2=8.64ns
required time = (1.2+0.86)*0.9-0.35*1.1+clock_period=1.469+clock_period
那么由于required time-arrival time>=0则clock_period>=7.171,即最小时钟周期为7.171ns。可以看到,在加入最差情况的OCV后,电路能运行的时钟频率明显下降了。
但是在上面的计算中,我们还是可以发现一个问题,即common clock path即属于launch clock path,也属于capture clock path,所以在计算中,我们对其使用了不同的derate系数进行计算:在计算arrival time中,系数为1.2;在计算required time中,系数为0.9,这样会让我们的分析更为悲观,电路性能更差。而在真实的情况中,common clock path的PVT只有一个,不可能同时有两个derate系数,所以我们会进行CPPR操作。
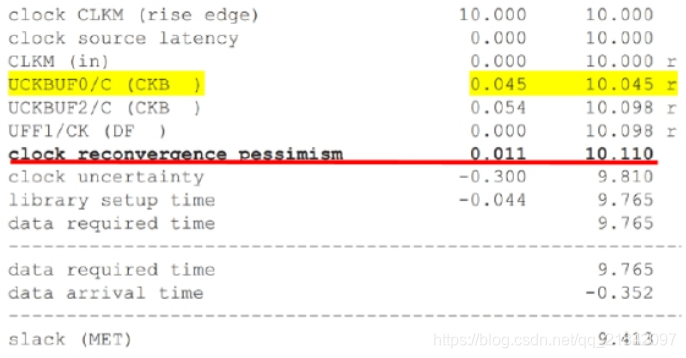
CPPR(Clock Path Pessimism Removal)或者CRPR(Clock Reconvergence Pessimism Removal),中文名“共同路径悲观去除”。它的作用是去除clock path上的相同路径上的悲观计算量,即我们上面提到的问题。我们将common point定义为时钟树上共同部分最后一个cell的output pin。则定义CPP因子为:
CPP=LatestArrivalTime@CommonPoint-EarliestArrivalTime@CommonPoint
我们进行CPPR后再来进行一次计算:
LatestArrivalTime@CommonPoint=1.2*1.2=1.44ns
EarliestArrivalTime@CommonPoint=1.2*0.9=1.08ns
CPP=1.44-1.08=0.36ns
则clock_period=7.171-0.36=6.811ns
可以看到,电路的运行时钟频率变好了一点,但对于未考虑OCV来说,整个运行时钟频率还是降低了。
我们可以来看看时序报告
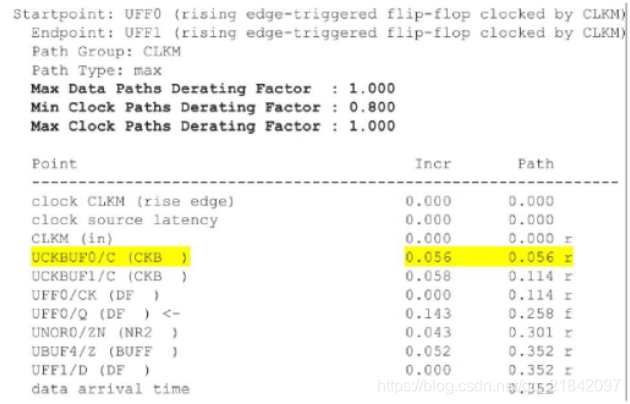
说完setup check,我们来看看OCV对hold check的影响。
进行hold check时,最差的情况为:launch clock path 和data path由于OCV的原因,延迟减小到最小;于此同时,capture clock path 由于OCV的原因,延迟增加到最大。此时,对保持时间的检查最为严苛。我们进行同样的分析,可以看到基本相同的结果。
其时序报告如下:



![[转载]IIS7报500.23错误的解决方法](http://pic.xiahunao.cn/[转载]IIS7报500.23错误的解决方法)





)


)








Hibernate高级配置)