一、概述

        引导滤波是由何恺明等人于2010年发表在ECCV的文章《Guided Image Filtering》中提出的，后续于2013年发表。引导过滤器根据局部线性模型原理，通过考虑引导图像的内容来计算过滤输出，引导图像可以是输入图像本身或另一个不同的图像。具有以下特点：

1. 引导滤波器可以像流行的双边滤波器一样用作边缘保留平滑算子，但在边缘附近有更好的效果。
2. 引导过滤器也是平滑之外的一个更通用的概念：它可以将引导图像的结构传输到过滤输出，从而实现新的过滤应用，例如去雾和引导羽化。
3. 此外，无论核大小和强度范围如何，引导滤波器自然具有快速且非近似的线性时间算法。目前它是最快的边缘保留滤波器之一。

Research:

• Wikipedia中指出，引导过滤器是一种具有代表性的边缘保持平滑技术。
• MATLAB 2014中提供了引导过滤器在这一新函数。
• OpenCV 3.0中提供了引导过滤器在这一新函数。

Related Publications:

• Guided Image Filtering, by Kaiming He, Jian Sun, and Xiaoou Tang, in ECCV 2010 .

• Guided Image Filtering, by Kaiming He, Jian Sun, and Xiaoou Tang, in TPAMI 2013.

See Also:

• Fast Guided Filter, by Kaiming He and Jian Sun, in arXiv 2015.

Resources:

• ECCV 2010 presentation slides

• Guided Filter: Code

• Fast Guided Filter: Code

二、原理

        引导滤波的定义中，用到了局部线性模型，该模型认为，某函数上一点与其邻近部分的点成线性关系，一个复杂的函数就可以用很多局部的线性函数来表示，当需要求该函数上某一点的值时，只需计算所有包含该点的线性函数的值并做平均即可。我们可以将图像看成一个二维函数，因此，而且没法写出解析表达式，因此我们假设该引导滤波函数的输出与输入在一个二维窗口内满足线性关系，如下：

        

        这里p是输入图像 ，I是引导图像 ，q是滤波输出图像， ak和bk是系数, ωk是窗口。

        对上式两边取梯度，可以得到：

            

        即当引导图像I有梯度时，输出 图像q 也有类似的梯度，现在可以解释为什么引导滤波有边缘保持特性。

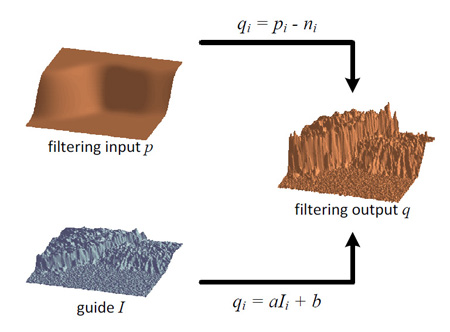
         接下来需要计算ak和bk，我们将输入图像p纳入考虑范围中，根据一般的加性噪声模型，我们很容易得到以下式子：

        

        其中ni表示需要去除的噪声或纹理。

        显然，我们现在要找到一个解能够最小化输出图q和输入图p的差别。定义代价函数如下：

                

         这里，是正则化参数，我们对代价函数求最小值，

        

         令偏导为0，计算得到：

             

         其中pk和uk分别是P和I窗口内的均值。 得到bk，我们再求ak

                  根据方差和协方差公式，

                 

           最终计算得到：

                  

三、实现及效果

        引导滤波算法伪代码如下图：

实际测试结果如下：