模意义下的FFT算法

//写在前面单就FFT算法来说的话，下面只给出个人认为比较重要的推导，详细的介绍可参考　　FFT算法学习笔记

令v[n]是长度为2N的实序列，V[k]表示该实序列的2N点DFT。定义两个长度为N的实序列g[n]和h[n]为

g[n]=v[2n],　　h[n]=v[2n+1],　　0<=n<N

则可进行如下推导

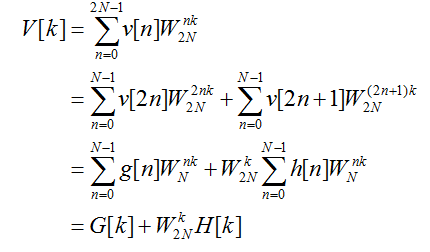
这里所用的FFT算法能够实现O(nlogn)复杂度的离散傅里叶变换和上面最后所得的关系密切相关。

下面进入正题——模意义下的FFT

还是需要先了解一下关于复序列的DFT的对称性质及一些补充定义

由此，可以试想，假设说要模的素数p为1e8级别大小，那么我们可以把原始的实序列x[n]“拆”一下。

下面假设我们要求的是x[n]卷积y[n]的结果t[n]。

假设q是sqrt(p)级别的一个数，我们可以把x[n]/q存到复序列x1[n]的实部，x[n]%q存到复序列x1[n]的虚部。这时，对x1[n]、y1[n]求DFT，再由X1[k]*Y1[k]得到T1[k],整个运算过程中能够产生的最大浮点数为N*q^2级别，一般来说还是在可以接受的范围内的。

接下来考虑从卷积结果{T1[k]}中恢复出原始的t[n]的过程。

看一下T1[k]的组成

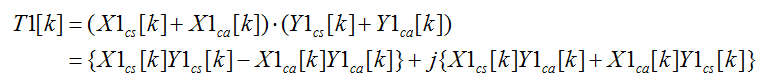
到这里差不多就可以结束了。发现上面最后一行等号右边有四个“乘积”，我们可以把上面四个乘积分别单独拿出来，求IDFT就可以恢复出x/y_re/im卷积的结果，之后针对不同的乘积，考虑需要在模p意义下乘上q^2、q^1或q^0，来进行恢复就可以了。

奉上模板

namespace FFT_MO    //前面需要有 mod(1e8~1e9级别),upmo(a,b) 的定义 
{const int FFT_MAXN=1<<18;const db pi=3.14159265358979323846264338327950288L;struct cp{db a,b;cp(double a_=0,double b_=0){a=a_,b=b_;}cp operator +(const cp&rhs)const{return cp(a+rhs.a,b+rhs.b);}cp operator -(const cp&rhs)const{return cp(a-rhs.a,b-rhs.b);}cp operator *(const cp&rhs)const{return cp(a*rhs.a-b*rhs.b,a*rhs.b+b*rhs.a);}cp operator !()const{return cp(a,-b);}}nw[FFT_MAXN+1],f[FFT_MAXN],g[FFT_MAXN],t[FFT_MAXN];    //a<->f,b<->g,t<~>c int bitrev[FFT_MAXN]; void fft_init()    //初始化 nw[],bitrev[] 
    {int L=0;while((1<<L)!=FFT_MAXN) L++;for(int i=1;i<FFT_MAXN;i++)  bitrev[i]=bitrev[i>>1]>>1|((i&1)<<(L-1));for(int i=0;i<=FFT_MAXN;i++) nw[i]=cp((db)cosl(2*pi/FFT_MAXN*i),(db)sinl(2*pi/FFT_MAXN*i));}// n已保证是2的整数次幂 // flag=1:DFT |  flag=-1: IDFTvoid dft(cp *a,int n,int flag=1)    {int d=0;while((1<<d)*n!=FFT_MAXN) d++;for(int i=0;i<n;i++) if(i<(bitrev[i]>>d))swap(a[i],a[bitrev[i]>>d]);for(int l=2;l<=n;l<<=1){int del=FFT_MAXN/l*flag;    // 决定 wn是在复平面是顺时针还是逆时针变化，以及变化间距 for(int i=0;i<n;i+=l){cp *le=a+i,*ri=a+i+(l>>1);cp *w=flag==1? nw:nw+FFT_MAXN;    // 确定wn的起点 for(int k=0;k<(l>>1);k++){cp ne=*ri * *w;*ri=*le-ne,*le=*le+ne;le++,ri++,w+=del;}}}if(flag!=1) for(int i=0;i<n;i++) a[i].a/=n,a[i].b/=n;}// convo(a,n,b,m,c) a[0..n]*b[0..m] -> c[0..n+m]void convo(LL *a,int n,LL *b,int m,LL *c){for(int i=0;i<=n+m;i++) c[i]=0;int N=2;while(N<=n+m) N<<=1;    // N是c扩展后的长度 for(int i=0;i<N;i++)    //扩展 a[],b[] ，存入f[],g[]，注意取模 
        {LL aa=i<=n?a[i]:0,bb=i<=m? b[i]:0;     aa%=mod,bb%=mod;f[i]=cp(db(aa>>15),db(aa&32767));g[i]=cp(db(bb>>15),db(bb&32767));}dft(f,N),dft(g,N);for(int i=0;i<N;i++)    // 恢复虚部两个“乘积”（乘积具体意义见上文）
        {int j=i? N-i:0;t[i]=((f[i]+!f[j])*(!g[j]-g[i])+(!f[j]-f[i])*(g[i]+!g[j]))*cp(0,0.25);}dft(t,N,-1);for(int i=0;i<=n+m;i++)    upmo(c[i],(LL(t[i].a+0.5))%mod<<15);for(int i=0;i<N;i++)    // 恢复实部两个“乘积”
        {int j=i? N-i:0;t[i]=(!f[j]-f[i])*(!g[j]-g[i])*cp(-0.25,0)+cp(0,0.25)*(f[i]+!f[j])*(g[i]+!g[j]);}dft(t,N,-1);for(int i=0;i<=n+m;i++)    upmo(c[i],LL(t[i].a+0.5)+(LL(t[i].b+0.5)%mod<<30));}
}