题目描述:
小A是一名DIY爱好者,经常制作一些有趣的东西。
今天,小A突然想要来做这样一个东西。小A现在有两块同样大小为n×m,有n×m块大小为1×1小电路板拼成的矩形电路板,假设叫做电路板A和电路板B。电路板A上每个小电路板都是一个开关,电路板B上每个小电路板上都是一盏电灯泡。A与B之间存在如下关系:对于B上的某盏灯Bij的开关控制,有A上第i行与第j列所有开关并联控制。即:
现给一矩阵,表示B上灯泡的明暗状态,问是否存在一种A的开关状态,能够满足给出的B上的灯泡开关情况,如果有输出YES,没有输出NO。
输入描述:
第一行,n和m表示电路板的长和宽,(1<=n,m<=1000)
接下来n行,每行有m个由空格隔开的数字,0或1。0表示灯泡暗,1表示灯泡亮
输出描述:
输出一行,如果存在至少一种A的开关设置方式,能够使得B上灯泡明亮和给出的状态矩阵相同,则输出YES;不存在则输出NO。
示例:
样例1:
输入:
2 3
1 1 1
1 1 1
输出:
YES
样例2:
输入:
2 3
1 1 0
0 1 1
输出:
NO
思路
我的想法是可以不判断开关状态,直接判断灯的状态,因为根据电路知识可以得到,一个a[i][j]开关打开将导致b中[i]行和[j]列所有的灯的打开(一个十字交叉)
因此只需要判断b是否满足这种十字交叉的分布
也就是如果b某个元素为true 则他对应的一行或者一列必须为true 不满足直接输出NO(这里可以只遍历第一行和第一列,并计数满足条件的行和列)
全为true的行数和列数必须大于0(表明有交点,交点处该处a的开关打开) 不满足输出NO
代码整理后给出
另一个网友的代码:
https://blog.csdn.net/lizhentao0707/article/details/80964205
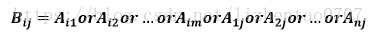








![[HAOI2008]移动玩具](https://images.cnblogs.com/OutliningIndicators/ExpandedBlockStart.gif)