在前面计算完损失后,该进行更新:
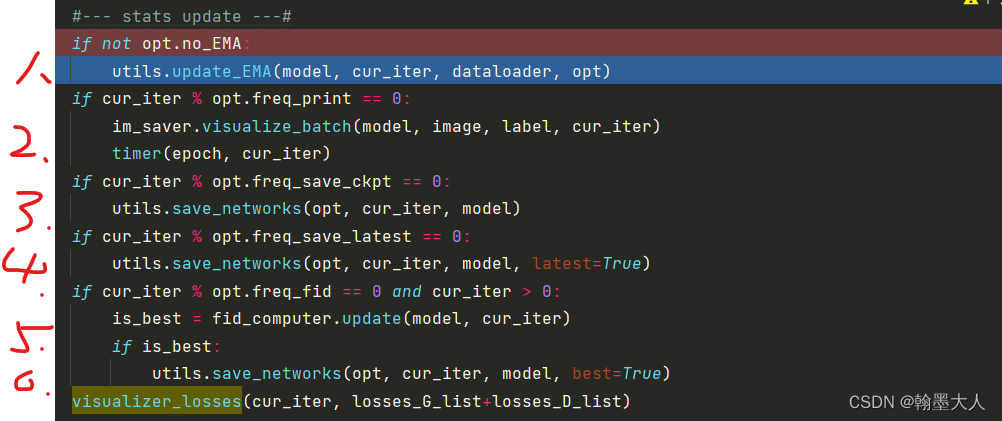
1:netEMA是模型的生成器:

遍历生成器的state_dict,将每一个键对应的值乘以EMA_decay。

接着根据当前迭代步数计算num_upd,每1000,2500,10000代倍数就执行一次。


当num_upd大于50就跳出更新EMA。
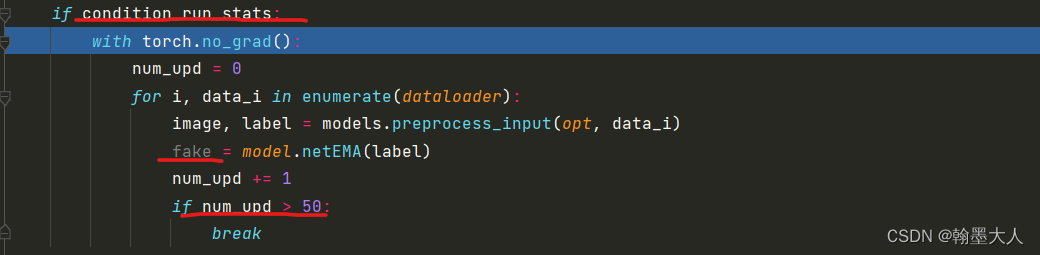
接着对图片进行上色:
def visualize_batch(self, model, image, label, cur_iter):self.save_images(label, "label", cur_iter, is_label=True)self.save_images(image, "real", cur_iter)with torch.no_grad():model.eval()fake = model.netG(label)self.save_images(fake, "fake", cur_iter)model.train()if not self.opt.no_EMA:model.eval()fake = model.netEMA(label)self.save_images(fake, "fake_ema", cur_iter)model.train()
首先对标签进行上色:
label即batch是经过one-hot编码后的标签大小为(5,35,256,512)。

接着len(batch)=5,取第一个batch对应的tensor。
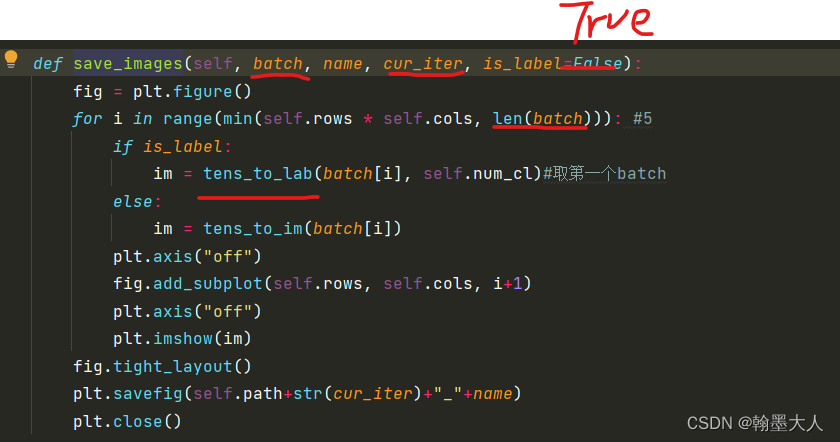
进行上色:
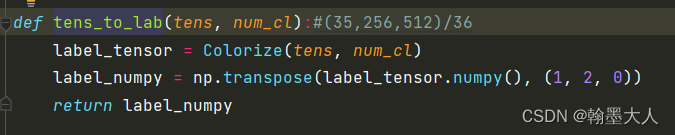
首先获得camp:
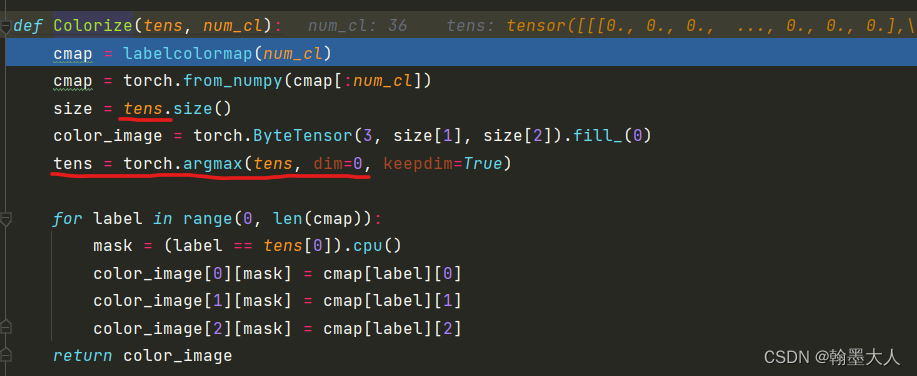
生成的colormap包含空像素和噪声,一共有36个类别,所以执行else语句。
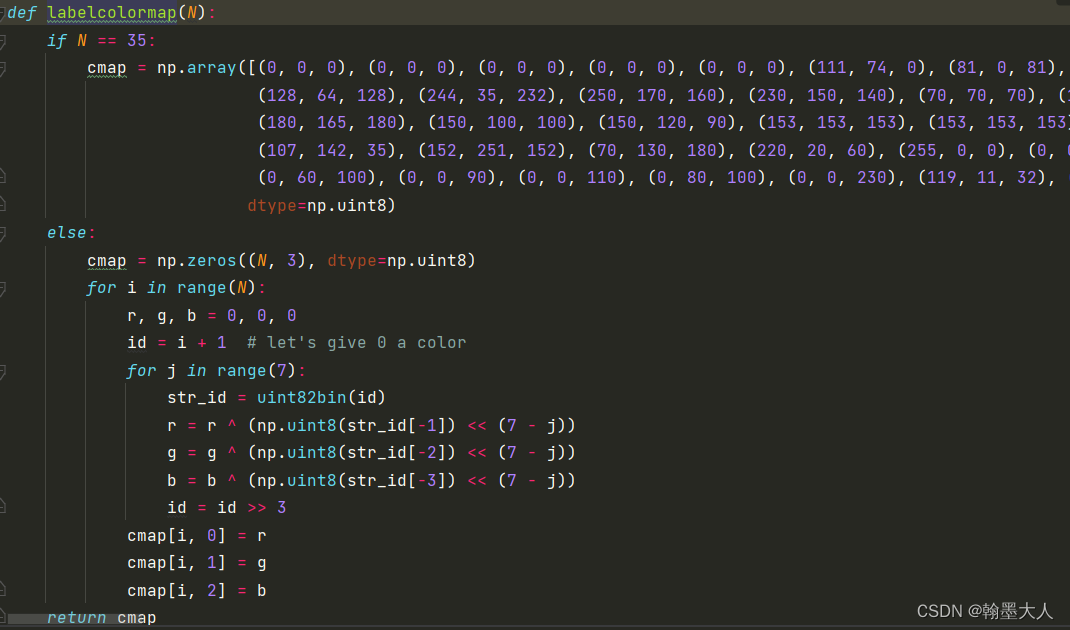
首先生成一个全为0的列表,大小为(36,3)—>接着遍历每个类别,初始化r=g=b=0—>id = 1—>接着遍历7次,首先将id转换为二进制类型。
def uint82bin(n, count=8):"""returns the binary of integer n, count refers to amount of bits"""return ''.join([str((n >> y) & 1) for y in range(count - 1, -1, -1)])
#y = 7,6,5,4,3,2,1,0
y分别取值为7,6,5,4,3,2,1,0。
将n右移位7位,n为1,则移位后为0,分别移位,只有当y等于0时,不移位,n才为1.最后返回一个字符串’00000001’.
移位操作
分别取str_id的倒数1,2,3位。然后将1,0,0分别左移七位,1左移后变为二进制为1000 0000即128.0左移后还是0,所以r=128,g=b=0.
最后id=1右移3位,变为0.
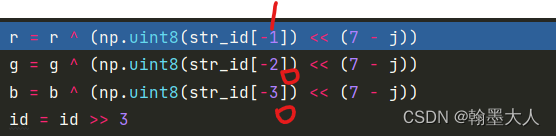
在j循环里执行8次,则下一次id=0.在uint82bin函数中,0不管位移多少次都为0,且0&1=0,所以最后输出’00000000’.
则r = 128^(0)=128.
因为128=(10000000),0=(00000000),(1异或0=1),(0异或0=0),所以128^(0)=128。这样执行7次后,将r填充为第一行第一列,g填充为第一行第二列,b填充为第一行第三列。这样执行for循环36次,则camp就会被重新填充一遍。
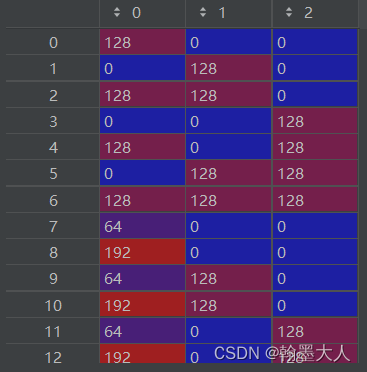
将camp转换为tensor。生成一个由0填充的(3,256,512)大小的size。同时对label的其中一个batch数据求类别。
tens大小由(35,256,512)变为(1,256,512)。

len(camp)=36,开始label=0时,tens[0]=(256,512),label==tens[0]会得到一个mask,其中tens中等于0的类别为True,不等于0的为false。
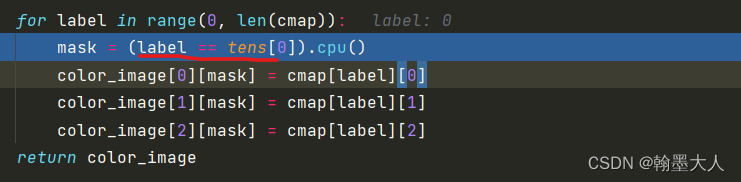
color_image[0]取得color_image第一层R通道,cmap[label][0]为第一行第一列即128,将mask对应的值全部替换为128.同理G和B通道也是这样处理。这样循环36次,将每一个类别都上色。最后输出经过填充的彩色图。

最后将label进行转置,方便cv2保存。
最后将batch剩余的四个图片也进行处理。将五张图放在一个图片上保存到指定位置。
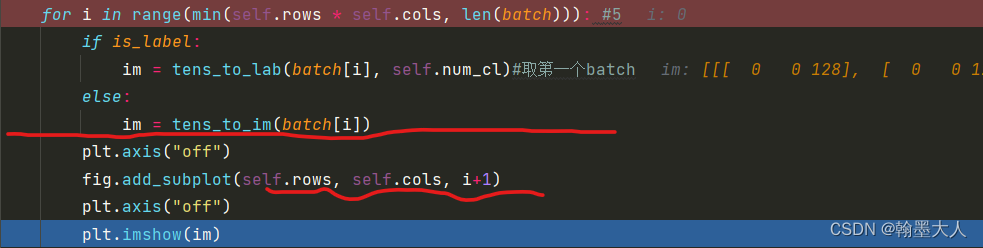
下一步对image处理:



将tens小于0的设置为0,大于1的设置为1.再转置为(h,w,c)格式。
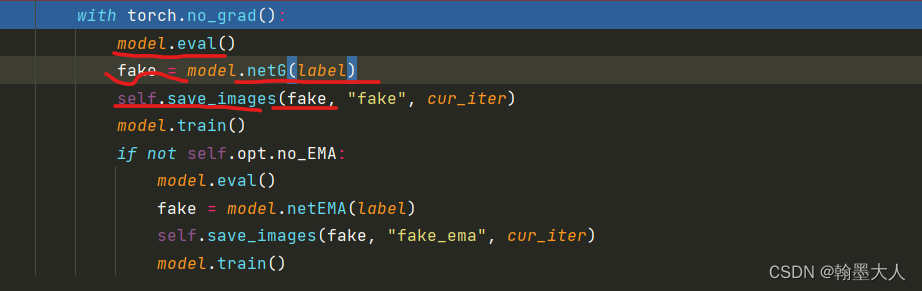
在eval时候,将label输入到生成器中,生成fake image,大小为(5,3,256,512)。将生成的fake image保存起来。

netEMA是对生成器的深拷贝。

下一步计算训练一个batch所需要的时间:

将epoch,总epoch,当前迭代,所花费的时间写到progress.txt文件中,并打印出来。
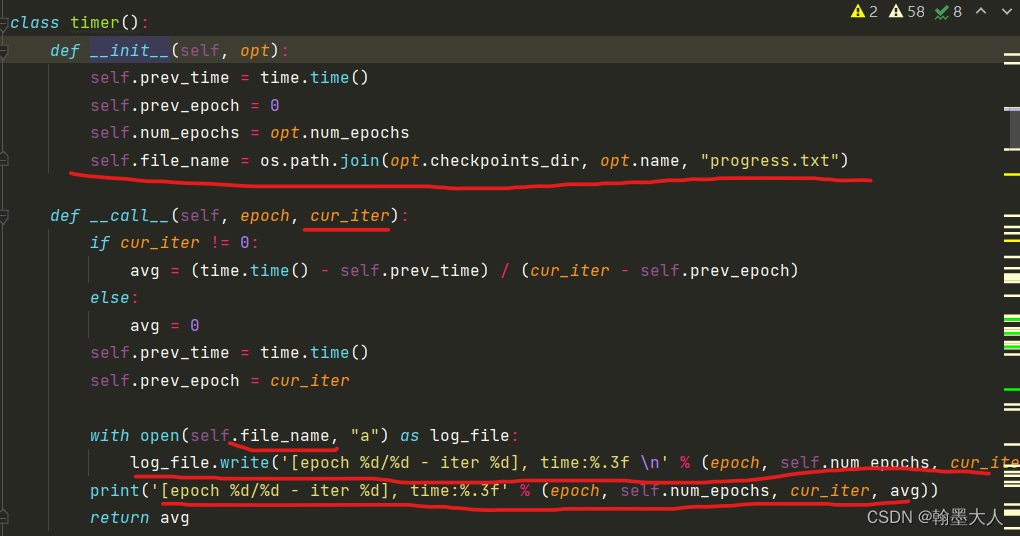
下一步:
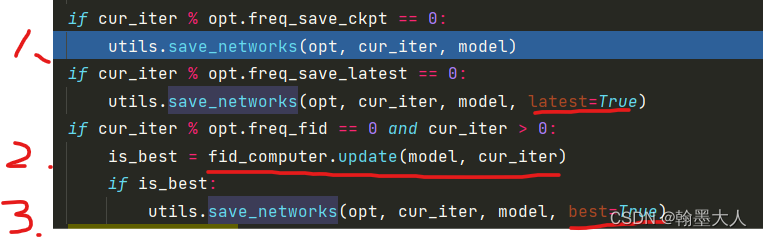
通过控制latest,best来保存权重。
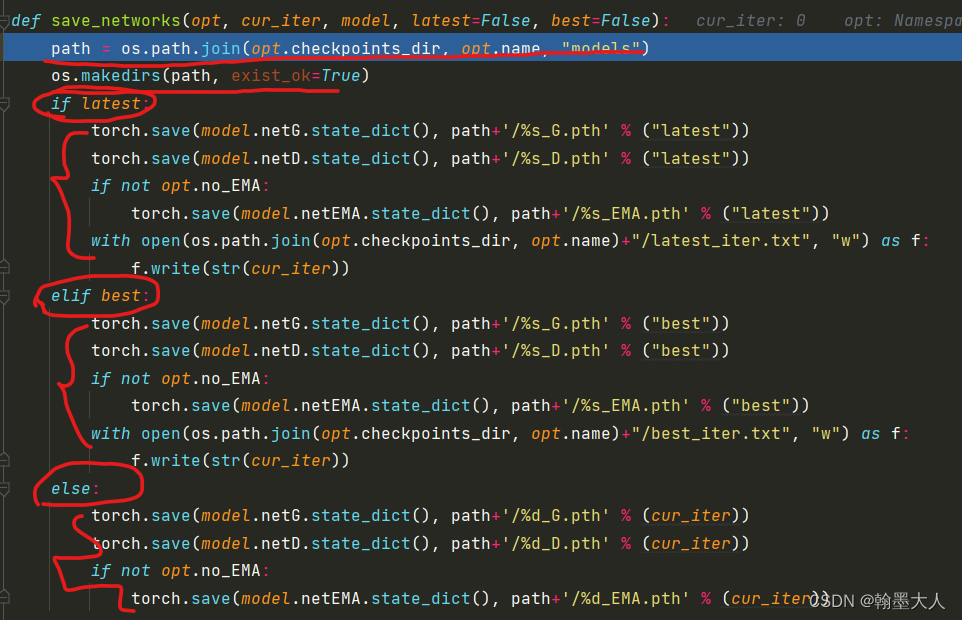
最重要看一下FID计算:比较麻烦,到时候重新开一章。








)
)






)

从入门到精通系列之十四:安装工具)
