1.简述
求解微分方程的时候,如果不能将求出结果的表达式,则可以对利用数值积分对微分方程求解,获取数值解。欧拉方法是最简单的一种数值解法。前面介绍过MATLAB实例讲解欧拉法求解微分方程,今天实例讲解欧拉法求解一阶微分方程组。
本文理论部分来自知乎作者云端之下的文章“常微分方程——数值解——欧拉方法”
微分方程的求解方法有解析解法和数值解法,解析法是求出因变量关于时间 �的具体函数式,表达 ;数值法是解出因变量 关于时间 �的离散序列,通常表达离散数据对。绝大多数的非线性常微分方程,不存在或难以求出解析解,大多数情况下只能求取微分方程的数值解。
2.代码
%% 学习目标:欧拉法求解微分方程组
clear;clc
c=2/3; %设置c的值
x(1)=0.1; %设置x初值为0.1
y(1)=0.3; %设置y初值为0.3
h=0.05; %设置步长为0.05
%for循环:根据Euler法,求解微分方程组
for i=1:1000
x(i+1)=x(i)+h*(x(i)*(c-x(i)/y(i)));
y(i+1)=y(i)+h*(y(i)*(1-y(i))-x(i)*y(i));
end
t=0:h:1000*h; %计算时间
plot(t,x) %绘制x曲线
hold on
plot(t,y,'r') %绘制y曲线
xlabel('time') %设置x轴的标签
ylabel('value') %设置y轴的标签
legend({'x','y'}) %设置图例
title('time evolution plot') %设置图形的标题
figure
plot(x,y) %绘制phase图
title('phase plane plot') %设置标题
xlabel('x') %设置x轴的标签
ylabel('y') %设置y轴的标签
3.运行结果

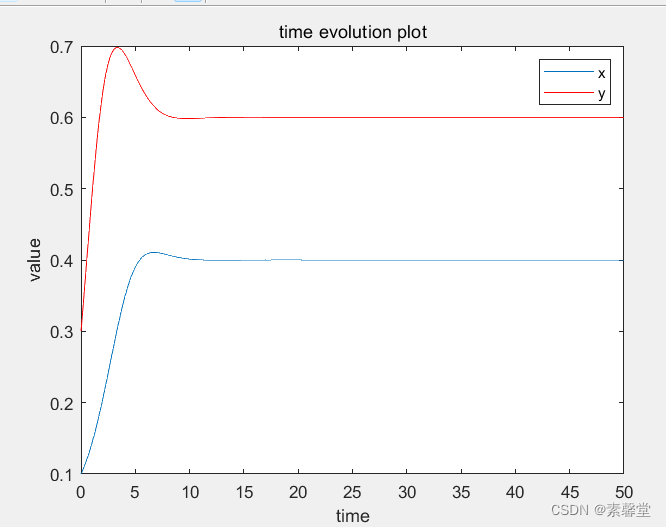
)
的源码说明)






方法可能导致的问题)










