力扣日记：【二叉树篇】236. 二叉树的最近公共祖先
日期：2023.12.24
参考：代码随想录、力扣
ps：提前祝 平安夜快乐！
236. 二叉树的最近公共祖先
题目描述
难度：中等
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例 1：
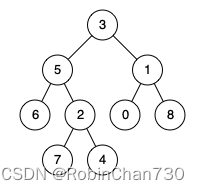
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：
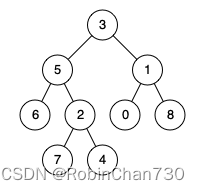
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：
输入：root = [1,2], p = 1, q = 2
输出：1
提示：
- 树中节点数目在范围 [2, 10^5] 内。
- -10^9 <= Node.val <= 10^9
- 所有 Node.val 互不相同 。
- p != q
- p 和 q 均存在于给定的二叉树中。
题解
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:// 本题要找两个子节点的最近公共祖先，是一个从底往上找的过程(先找到子节点才能找其祖先)// 而要从底往上查找->想到是回溯->想到二叉树遍历中的天然回溯,即后序遍历(左右中,根据左右节点的返回值处理中节点逻辑)// 且从底往上找，则先找到的公共祖先一定是最近公共祖先(深度最大)// 关于如何判断一个节点是节点q和节点p的公共祖先：// 第一种情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者反之，那么该节点就是节点p和q的最近公共祖先// 第二种情况：节点本身p(q)，是自己的祖先（实际上在代码实现中也包含在第一种情况中）// 递归参数与返回值：参数为当前节点与指定节点；返回值表示是否在当前节点的树中找到指定节点(或者找到公共祖先)TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {// 递归终止条件// 如果root为空节点了，则没有，返回空// 如果 root == q，或者 root == p，说明找到 q p ，则将其返回if (root == q || root == p || root == NULL) return root; // 如果根节点不为空或还没找到，则递归处理// 左(看左子树能不能找到p或q)TreeNode* left = lowestCommonAncestor(root->left, p, q);// 右(看右子树能不能找到p或q)TreeNode* right = lowestCommonAncestor(root->right, p, q);// 中(对左右返回值的处理逻辑)// 如果左右不为空，说明左子树返回一个，右子树返回一个，则当前root为公共祖先（情况1）if (left != NULL && right != NULL) return root;// 如果左为空而右不为空，说明右找到了一个或者直接找到公共祖先，返回右（包含了情况2）if (left == NULL && right != NULL) return right;// 反之亦然if (left != NULL && right == NULL) return left;// 如果都为空,则返回空return NULL;}
};
复杂度
时间复杂度：
空间复杂度：
思路总结
-
本题想了想没有思路www直接看的代码随想录的…
-
首先明确祖先的概念：一个节点，是 以该节点为根节点的树上的所有节点的祖先；关于最近公共祖先的概念则为题目所述
-
本题思路（实际上是代码注释）：
- 本题要找两个子节点的最近公共祖先，是一个从底往上找的过程(先找到子节点才能找其祖先)
- 而要从底往上查找->想到是回溯->想到二叉树遍历中的天然回溯,即后序遍历(左右中,根据左右节点的返回值处理中节点逻辑)
- 且从底往上找，则先找到的公共祖先一定是最近公共祖先(深度最大)
- 关于如何判断一个节点是节点q和节点p的公共祖先：
- 第一种情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者反之，那么该节点就是节点p和q的最近公共祖先
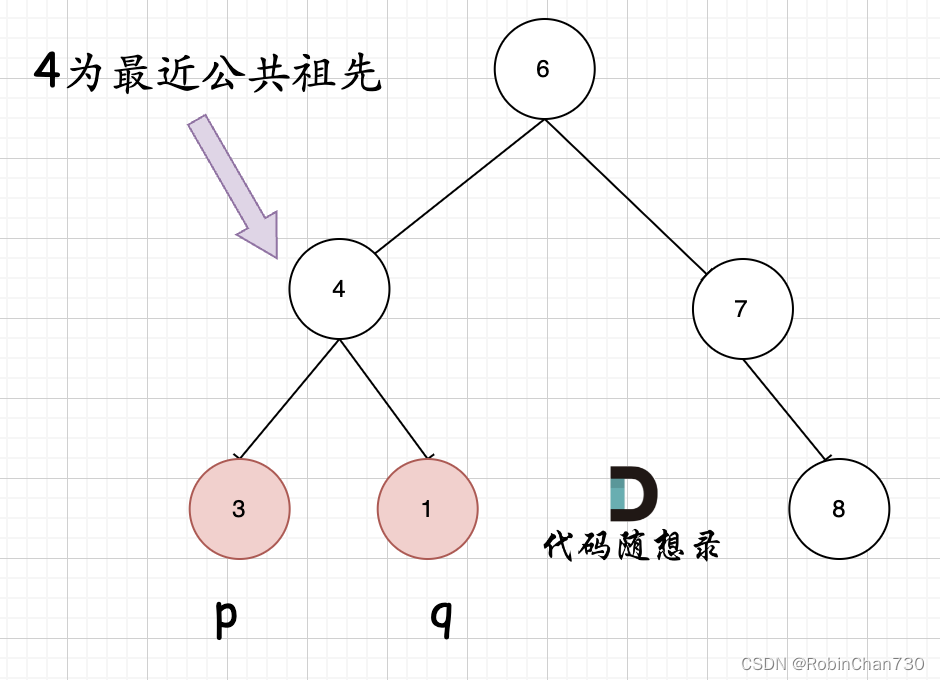
- 第二种情况：节点本身p(q)，是自己的祖先（实际上在代码实现中也包含在第一种情况中）
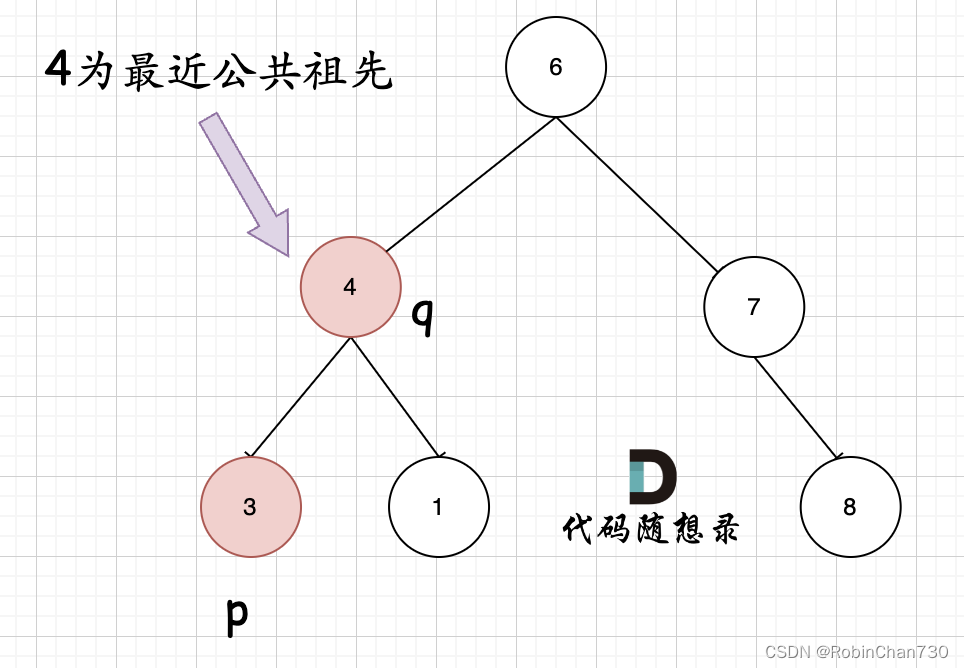
- 第一种情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者反之，那么该节点就是节点p和q的最近公共祖先
- 递归的三部曲：
- 递归参数与返回值：参数为当前节点与指定节点；返回值表示是否在当前节点的树中找到指定节点(或者找到公共祖先)
- 递归终止条件：
- 如果root为空节点了，则没有，返回空
- 如果
root == q，或者root == p，说明找到 q p ，则将其返回
- 递归处理逻辑：
- 如果根节点不为空或还没找到，则递归处理
- 左(看左子树能不能找到p或q)
- 右(看右子树能不能找到p或q)
- 中(对左右返回值的处理逻辑)
- 如果左右不为空，说明左子树返回一个，右子树返回一个，则当前root为公共祖先；（对应情况1）
- 如果左为空而右不为空，说明右找到了一个或者直接找到公共祖先，返回右（反之亦然）（包含了情况2，当然也对情况1的处理也可能有此步骤）
- 如果都为空,则返回空。
-
mark：之后再仔细看看 代码随想录中 关于返回值的描述。
在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。
且代码随想录对本题的解析也很清晰，可以再读读。
-
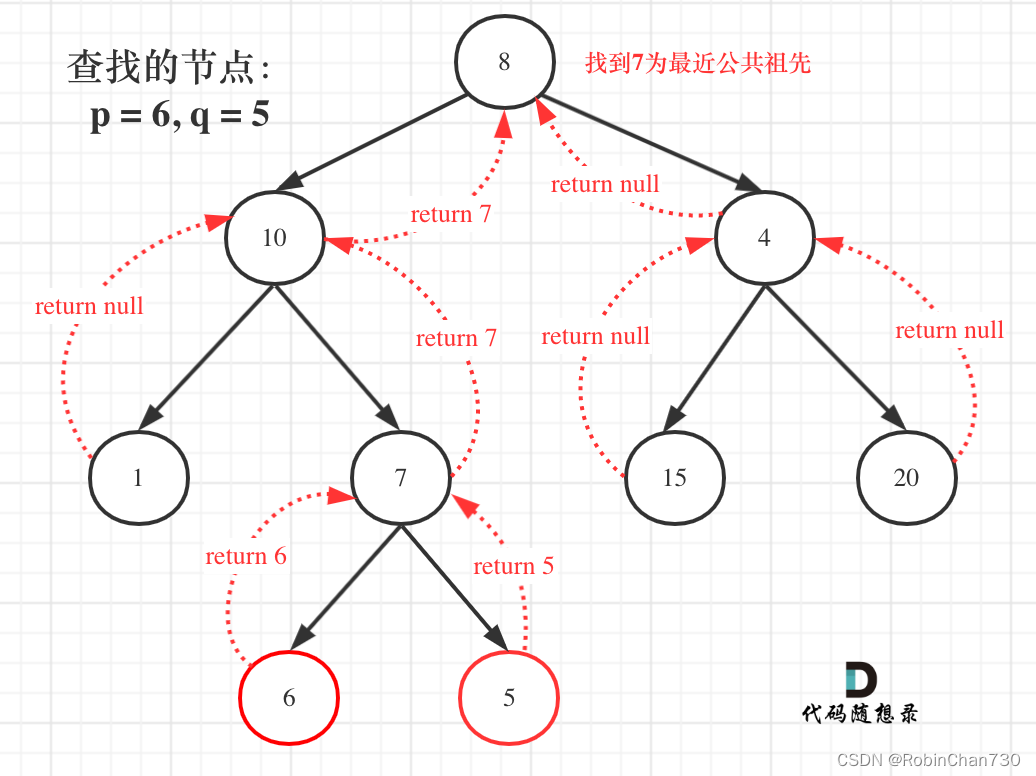
寻找最小公共祖先完整流程图如下：
