目录
- 决策树
- 是:
- Why:
- How:
- 基本概念
- 决策树生成
- 举例
- 决策树缺点
- 参考
- Demo
- 随机森林
- 1.是:
- 2.Why:
- 3.How:
- 参考
- Demo
决策树
是:
1.一种有监督的分类(或预测)算法。
2.利用属性、属性值构造一个决策的路径,可类比程序的if_else的多层判断。
如:利用贷款人信息预测是否会拖延还贷的一个简单决策树。
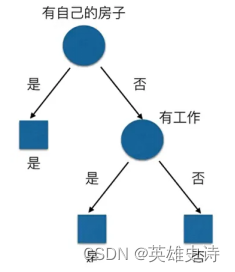
Why:
- 易于理解和解释。树可以被可视化。
- 几乎不需要数据准备。其他算法通常需要数据标准化,需要创建虚拟变量并删除缺失值。但是,请注意,此模块不支持缺失值。
- 使用树的成本(即预测数据)是用于训练树的数据点数的对数。 能够处理数值型和分类型数据。其他技术通常专门分析只有一种类型变量的数据集。
- 能够处理多输出问题。
- 使用白盒模型。如果给定的情况在模型中是可以观察到的,那么对条件的解释就很容易用布尔逻辑来解释。相反,在黑箱模型中(例如,在人工神经网络中),结果可能很难解释。
- 可以使用统计测试验证模型。这样就有可能对模型的可靠性作出解释。 即使它的假设在某种程度上被生成数据的真实模型所违背,它也表现得很好。
How:
基本概念
-
训练数据:用于训练模型的数据,英文是train。
-
测试数据:用于测试(验证)模型准确度的数据,英文是test。训练数据、测试数据都是来自已知的数据集,然后划分为2部分,一部分训练、一部分测试(验证),也就是在已知的数据集内完成训练和验证,才能去预测实战。
-
纯度、不纯度:根据某个属性分割数据集,样本类型的集中度,纯度越高越高。如按是否恒温划分是否哺乳动物,10个里9个是哺乳动物,纯度高;如按是否有毛发划分,则10个里有6个是哺乳动物,则纯度降低。是否恒温是更好的划分属性。常用的测算纯度的函数有基尼gini、熵entropy。、
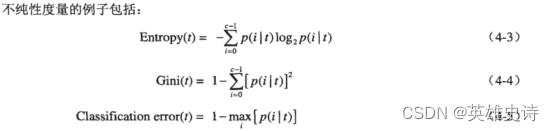
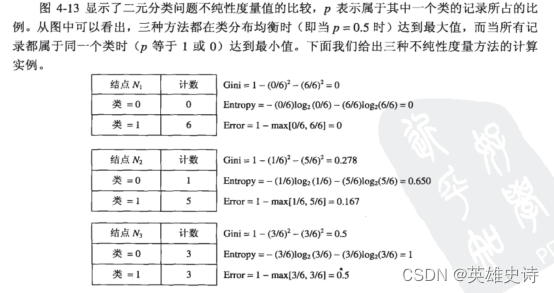
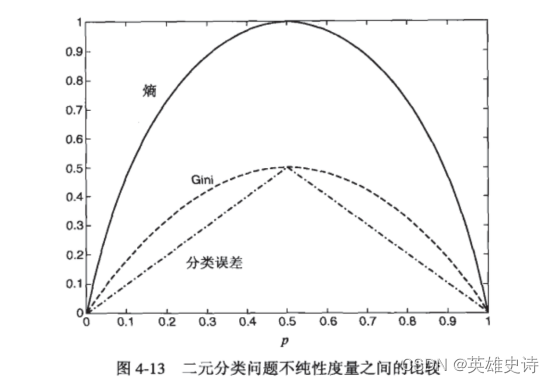
-
信息增益(information gain):对父节点,按属性再次划分后,纯度的增加量。
决策树生成
举例
-
数据集
样本个数10个,属性3个:有房者、婚姻、年收入;标签:是否拖欠贷款。
可以凭感觉,用if-else构造一个决策树。属性排序:有房者、婚姻、年收入。
问题:因为属性、属性性值、先后顺序,决策树有指数个肯能,哪个是最优?
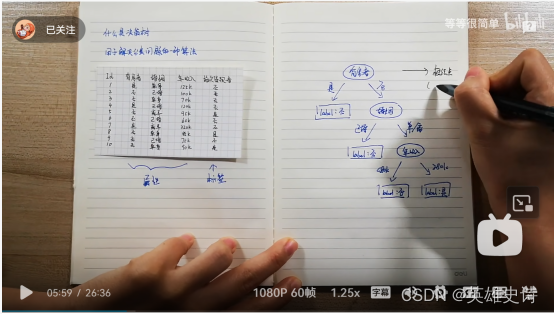
-
属性测算

婚姻属性的信息纯度最高。
3. 属性选择

类似,生成完整的树。与感性的分配有差异,属性排序:婚姻、有房者、年收入。
关键问题:如何选择属性、生成节点?
选择属性、按属性值分类、局部最优、信息增益最大。
后序以此类推。
决策树缺点
- 决策树学习器可以创建过于复杂的树,不能很好地概括数据。这就是所谓的过拟合。为了避免这个问题,必须设置剪枝、设置叶节点所需的最小样本数或设置树的最大深度等机制。
- 决策树可能是不稳定的,因为数据中的小变化可能导致生成完全不同的树。通过集成决策树来缓解这个问题。
- 学习最优决策树的问题在最优性的几个方面都是NP-complete的,甚至对于简单的概念也是如此。因此,实际的决策树学习算法是基于启发式算法,如贪婪算法,在每个节点上进行局部最优决策。这种算法不能保证返回全局最优决策树。这可以通过训练多棵树再集成一个学习器来缓解,其中特征和样本被随机抽取并替换。
- 有些概念很难学习,因为决策树不能很容易地表达它们,例如异或、奇偶校验或多路复用器问题。
- 如果某些类占主导地位,则决策树学习者会创建有偏见的树。因此,建议在拟合决策树之前平衡数据集。
参考
https://www.bilibili.com/video/BV1T7411b7DG/?spm_id_from=333.337.search-card.all.click&vd_source=1e37904a72db86b329d6b5320c86a013
Demo
酒分类预测:
https://github.com/heroicpoem/MachineLearningInAction/blob/master/decisionTree.ipynb
随机森林
1.是:
基于决策树的、集成算法。
森林,指包含多个决策树;
随机,指构造单棵决策树时,随机的选择样本,使得决策树是不同,或者侧重不同的能力。最后是整合多棵树的预测结果:均值或者众数。
2.Why:
- 随机决策森林纠正了决策树的过度拟合
- 随机森林通常优于决策树,但它们的准确性低于梯度提升树
- 更多的树会提高性能并使预测更稳定
- 抗噪
3.How:
构造多棵决策树,分别决策,整合结果。
2个超参:决策树个数、分几层、如何采样、结果整合方法。
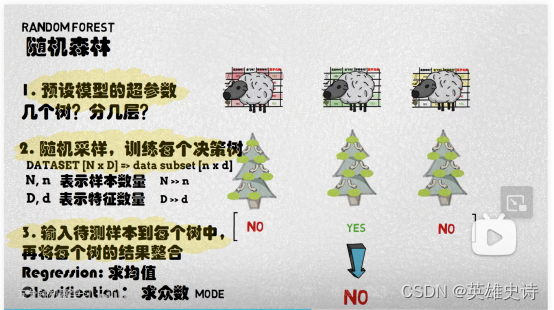
参考
https://www.bilibili.com/video/BV1H5411e73F/?spm_id_from=333.337.search-card.all.click&vd_source=1e37904a72db86b329d6b5320c86a013
Demo
https://blog.csdn.net/Graow/article/details/106749351


















)
