【ChatGPT】前些天发现了一个巨牛的人工智能学习电子书,通俗易懂,风趣幽默,无广告,忍不住分享一下给大家。(点击查看学习资料)
前段时间微软发的Microsoft 365 Copilot 可以说非常火爆了,那么该怎么抢鲜体验呢。今天分享的操作,目前大家不用急着来,因为订阅365还是要花钱的,大家可以等到真正能用的时候再开通。
如果你已经订阅了365,有时间可以按照这个步骤操作一下,早早排队。现在只是英文的,中文的还没出。
首先,打开自己的office word
点击左上角“文件”

点击左下角“账户

查看自己的账户是否有开通office 365
必须开通了才可以
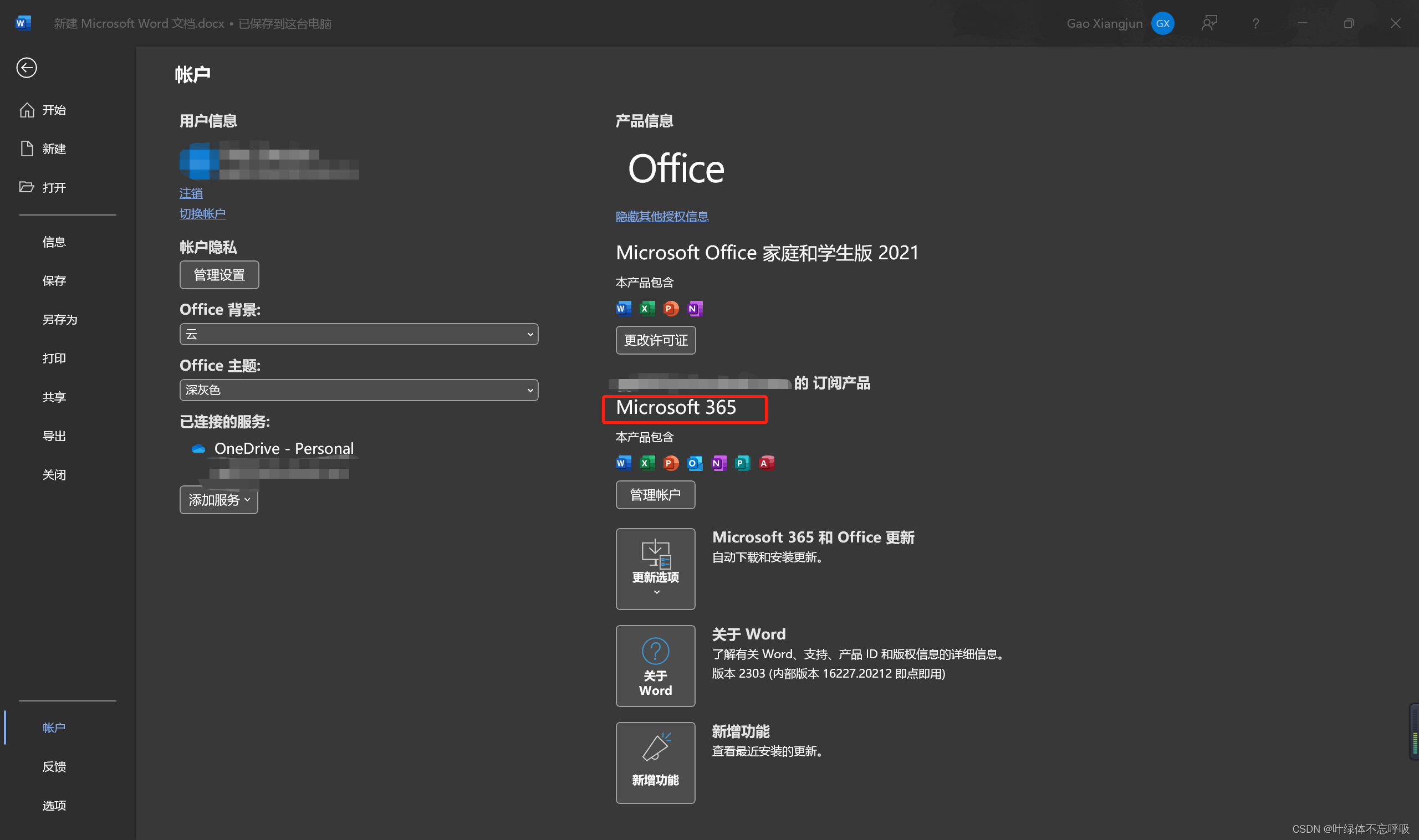
然后点击左下角:选项
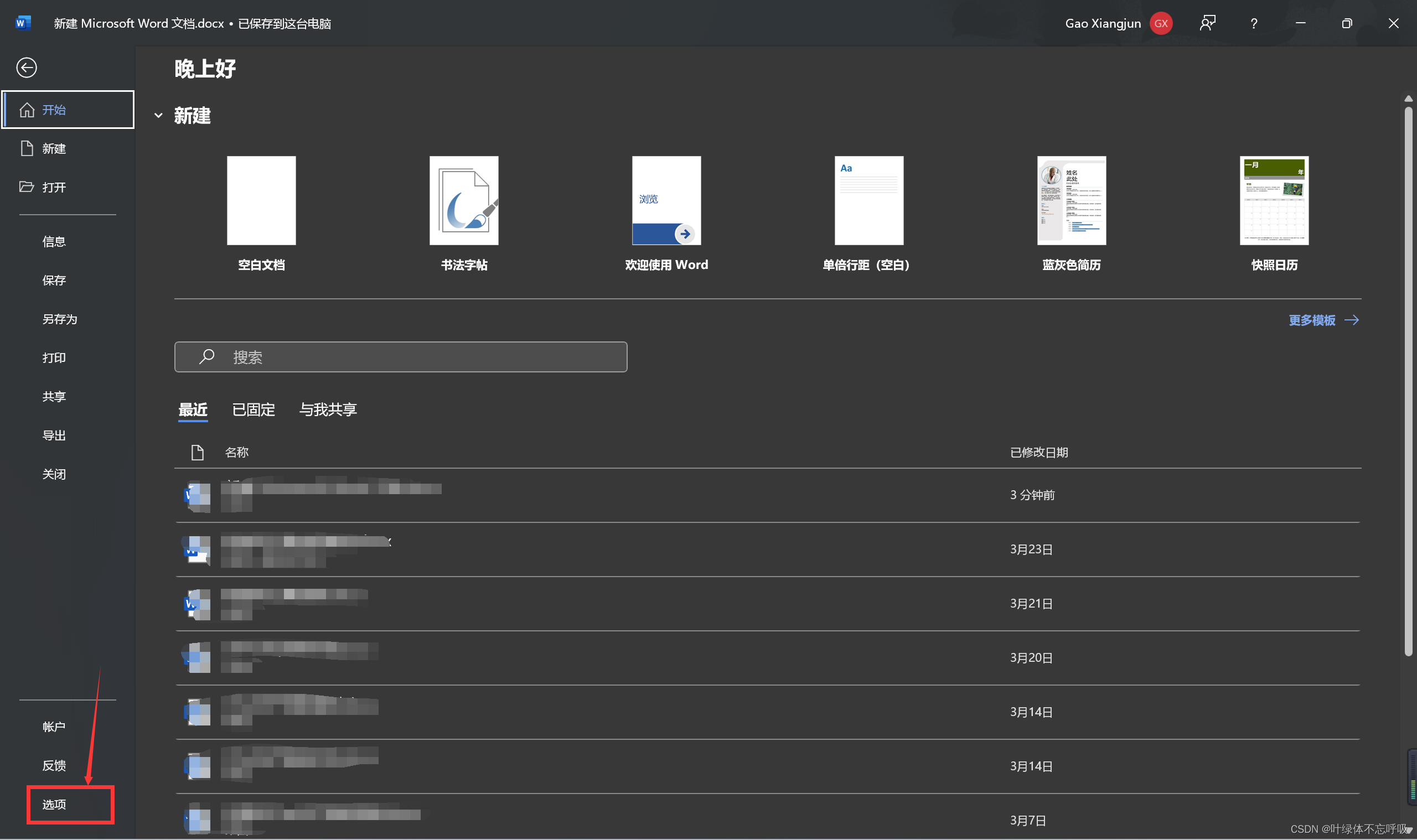
会弹出一个框
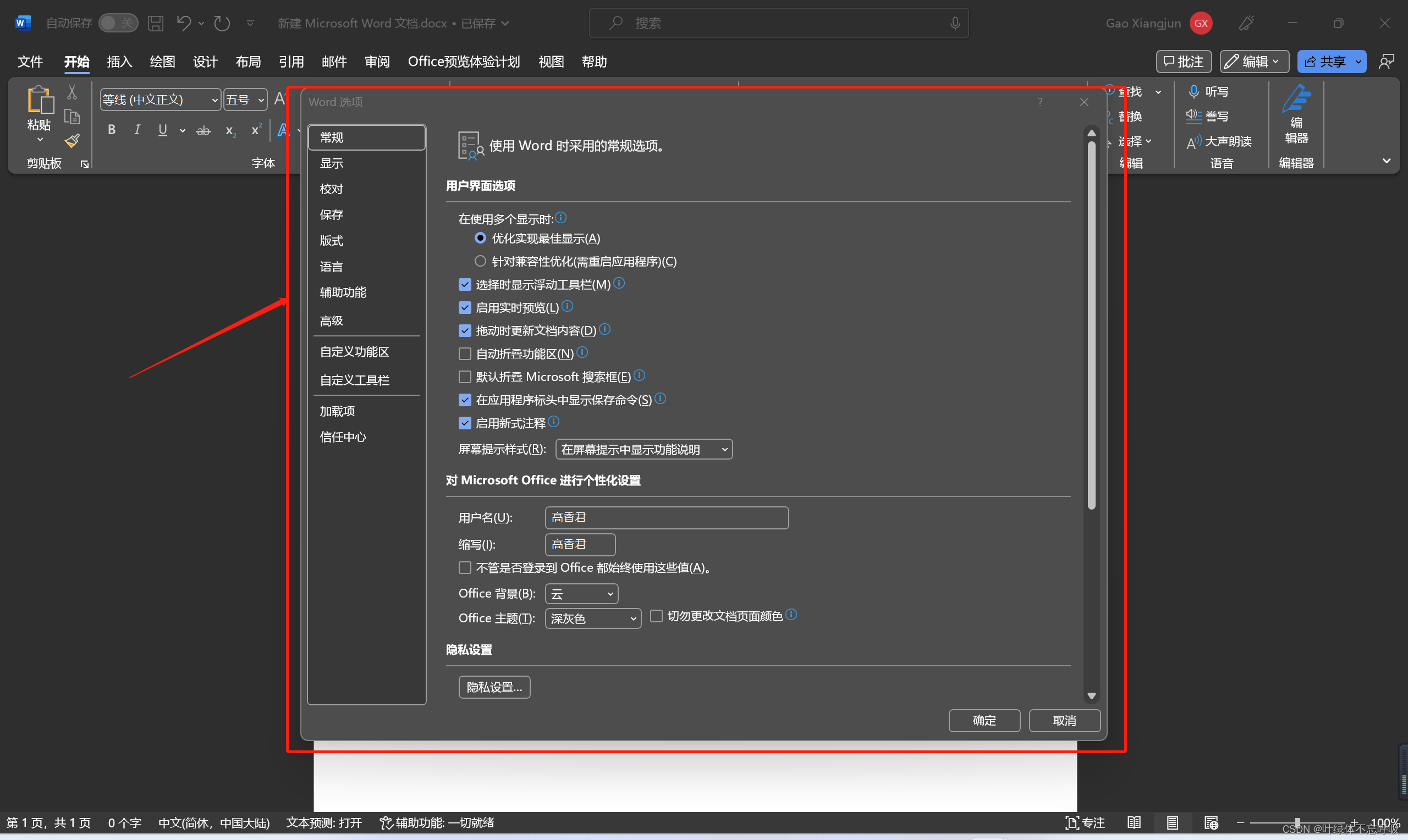
选择自定义功能区-左侧: 从下列位置选择命令:
切换到:不在功能区中的命令
如图所示
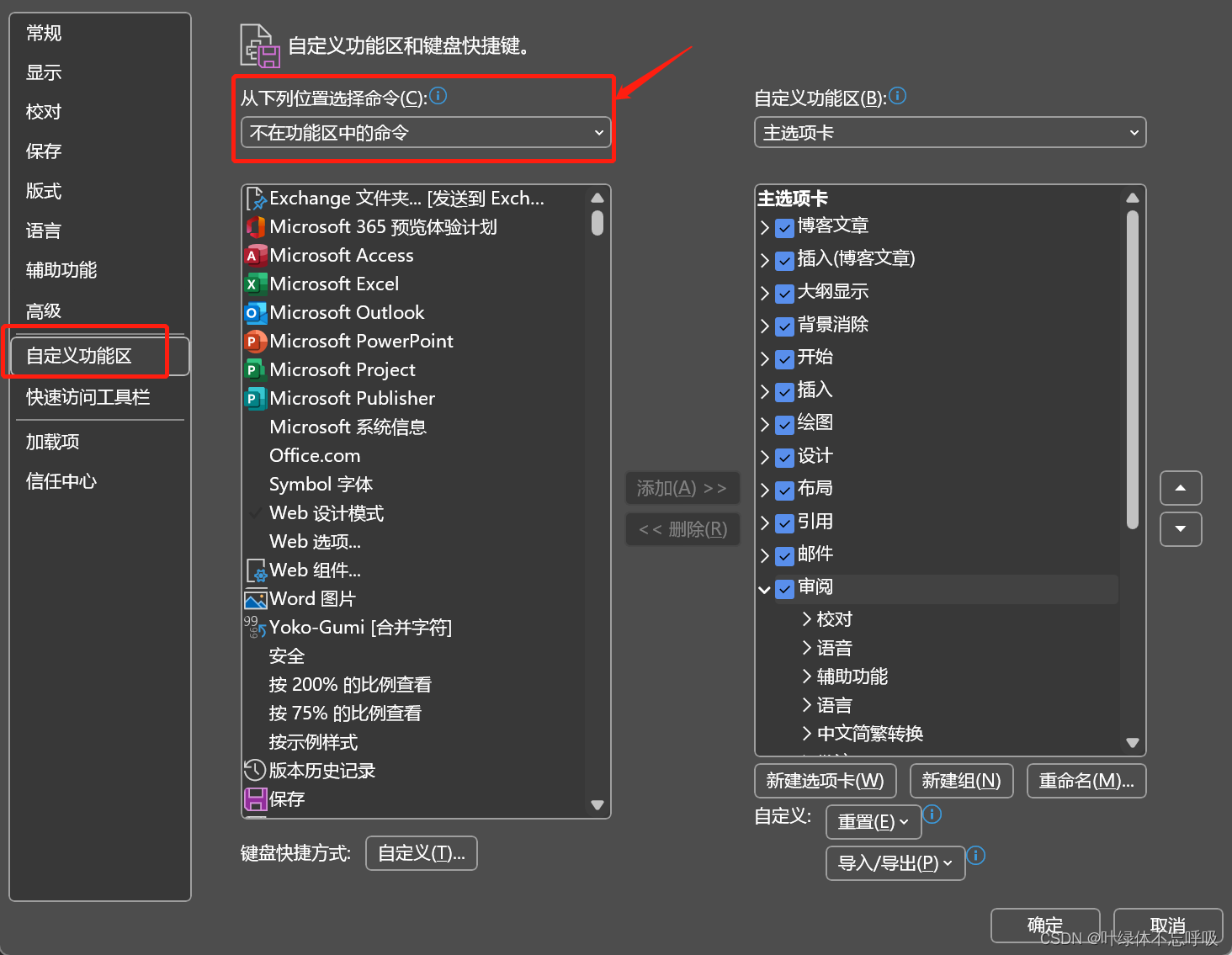
点击: 365 预览体验计划
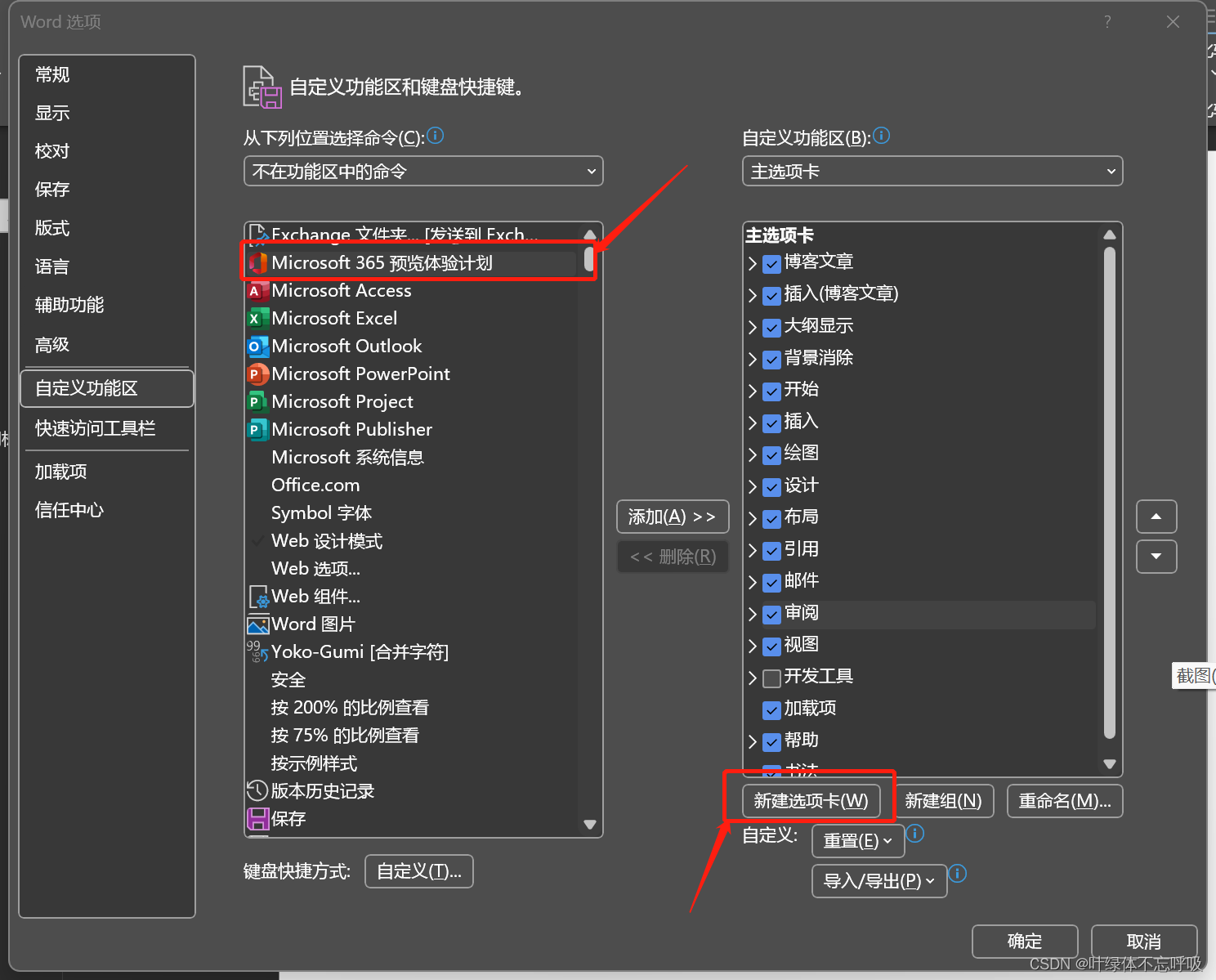
点击新建选项卡,
会多出来一个“新建选项卡 (自定义)”,然后点击重命名
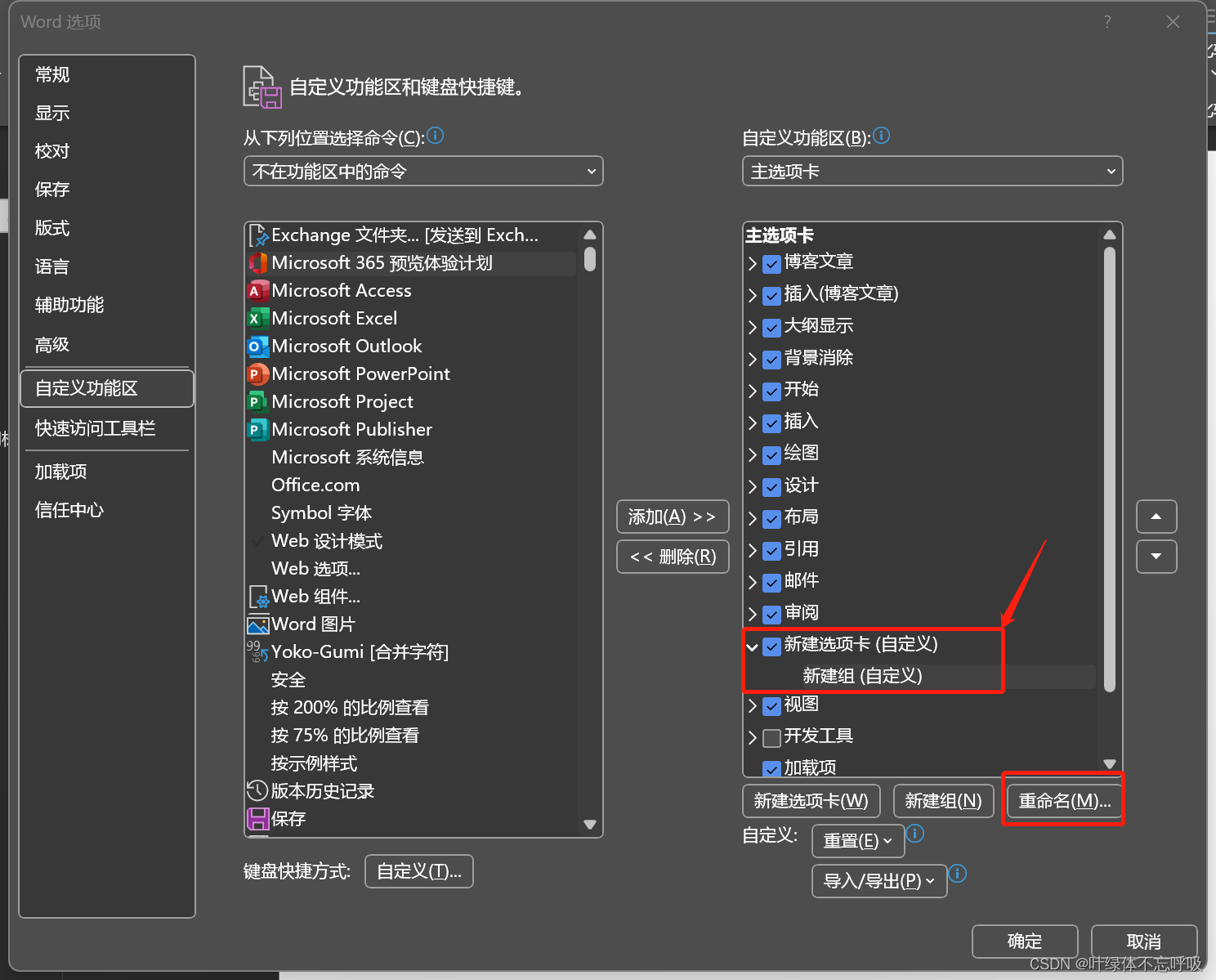
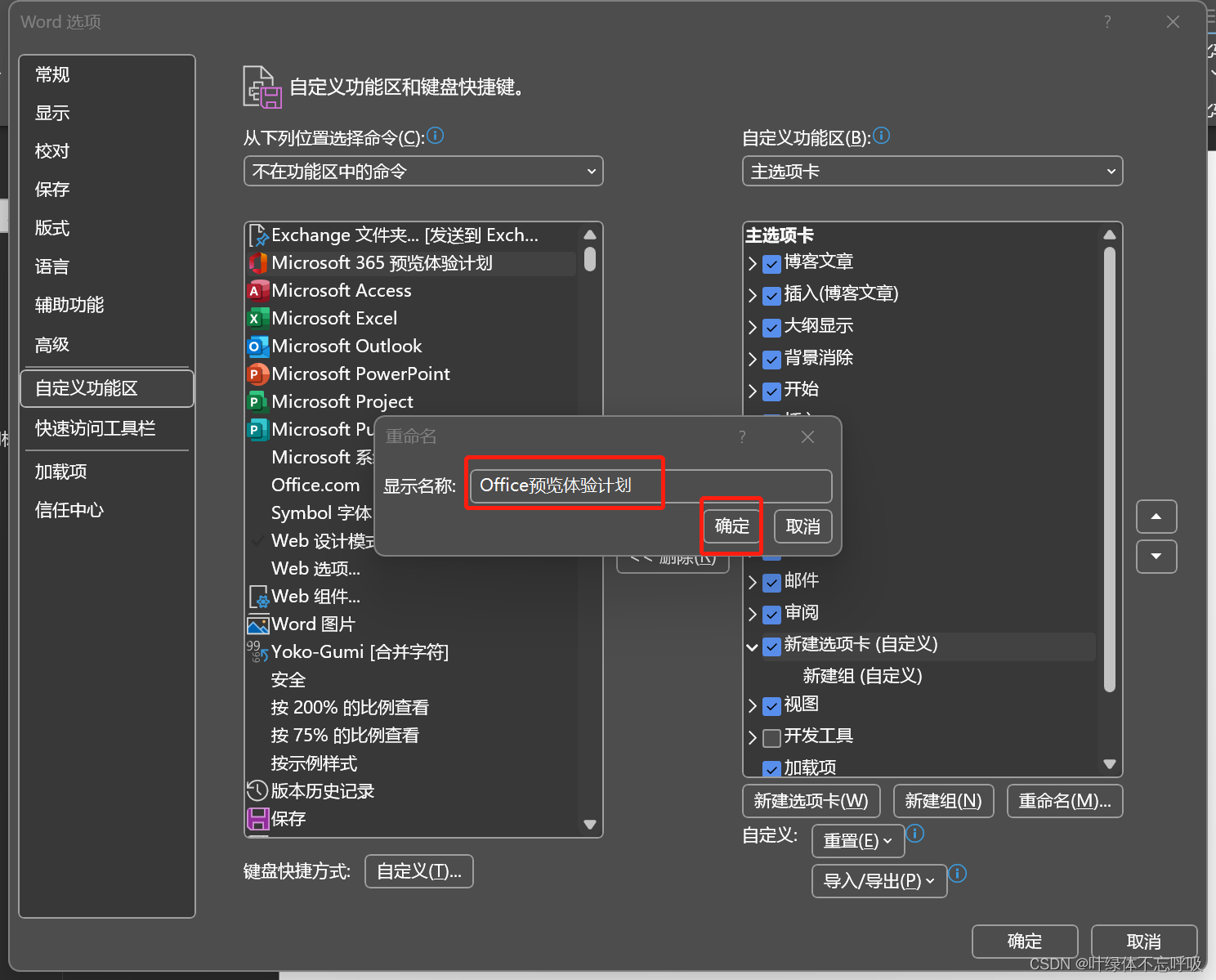
这里重命名为“Ofice预览体验计划”,点击确定
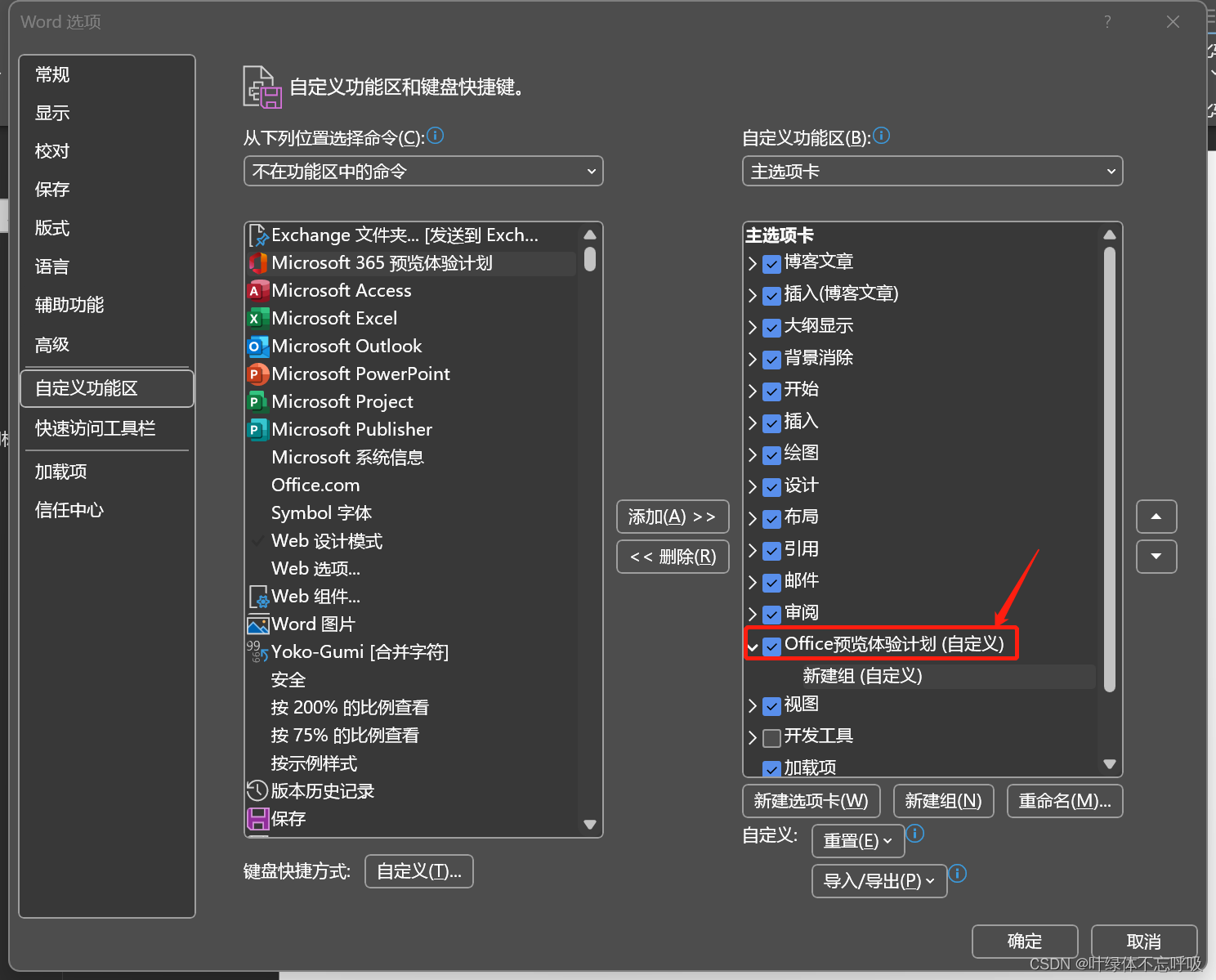
然后,按照下图挨个按按钮,看清楚顺序哦
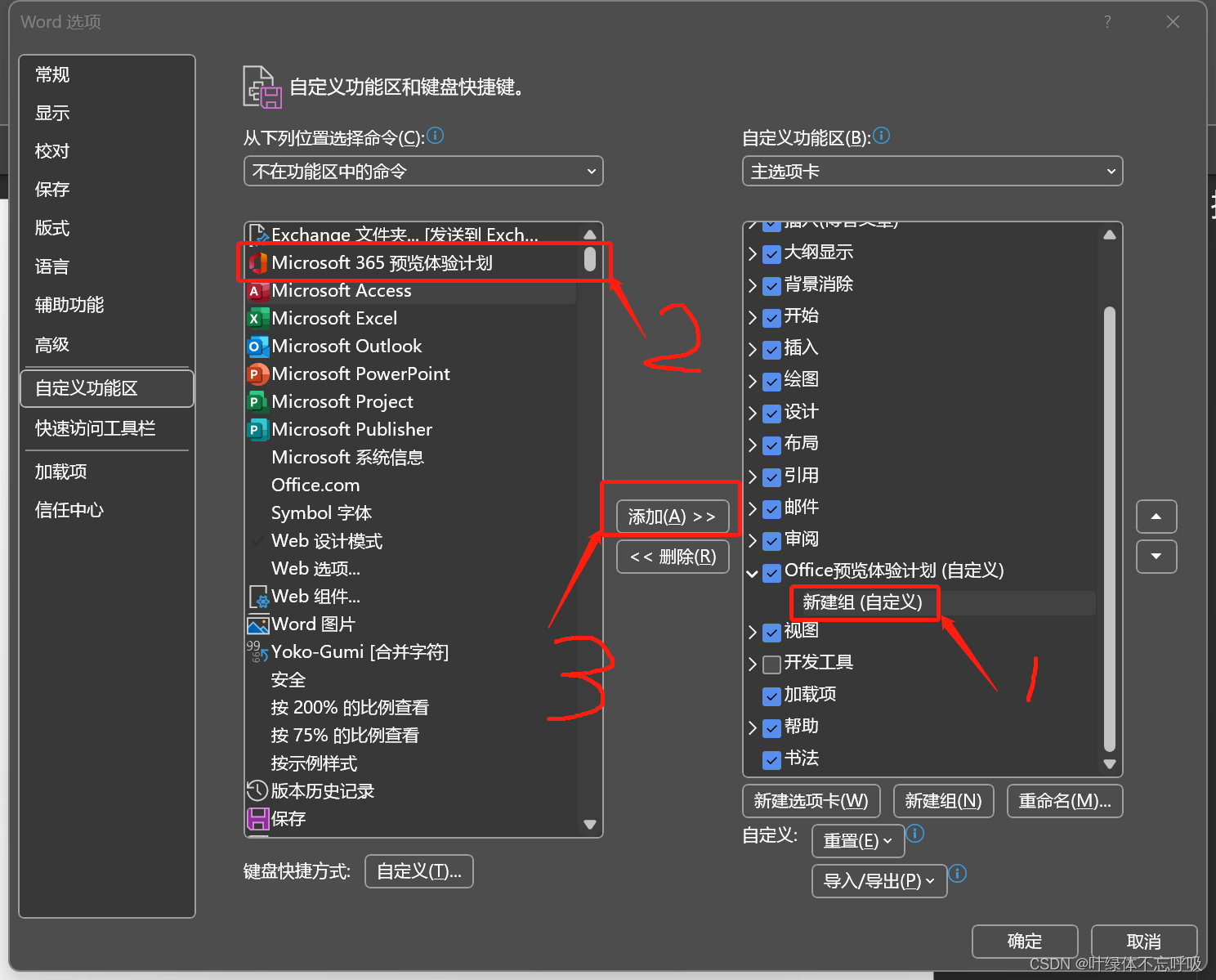
之后会看到这样的界面
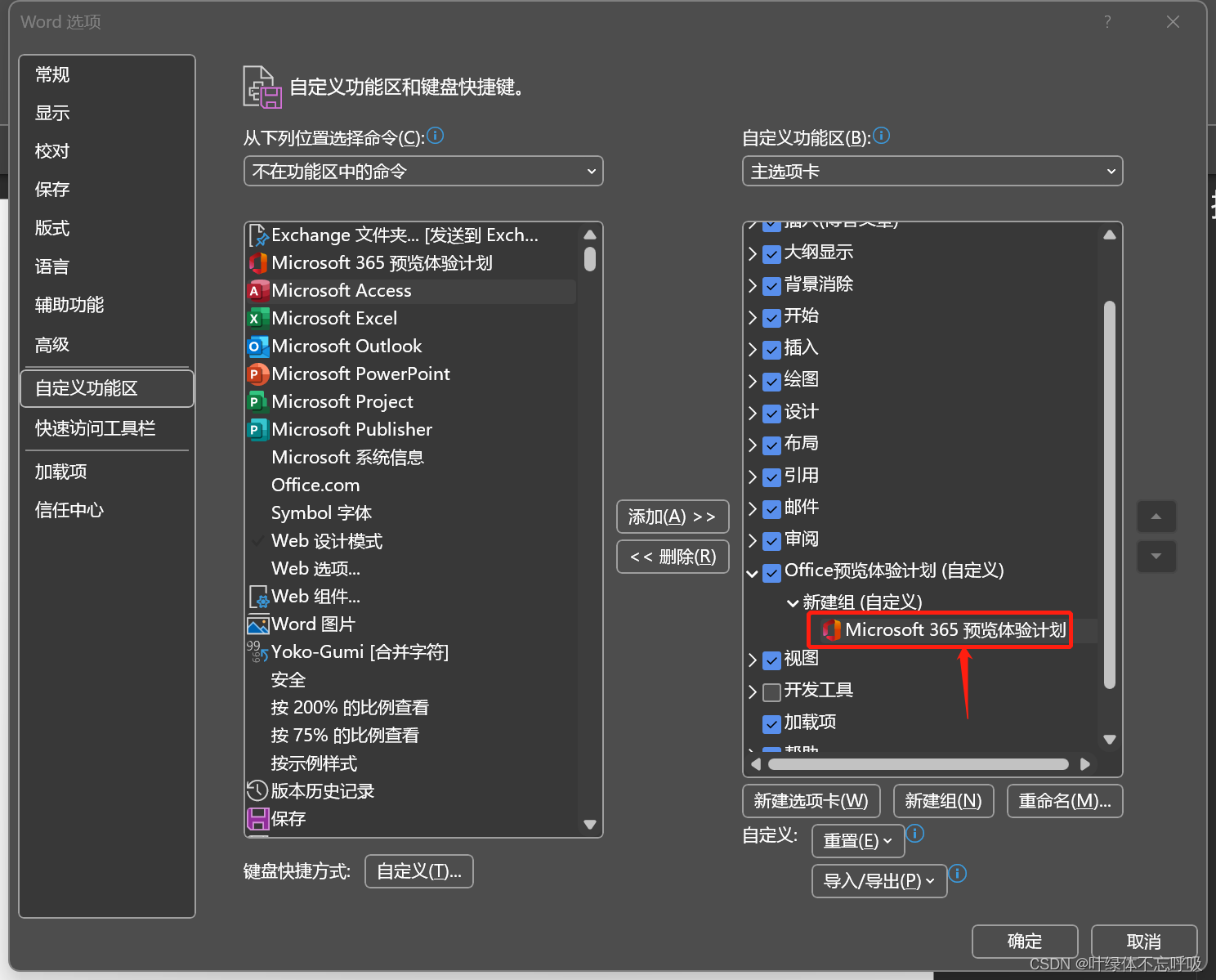
365预览计划添加到新建组下面了,点击确定右下角确定按钮
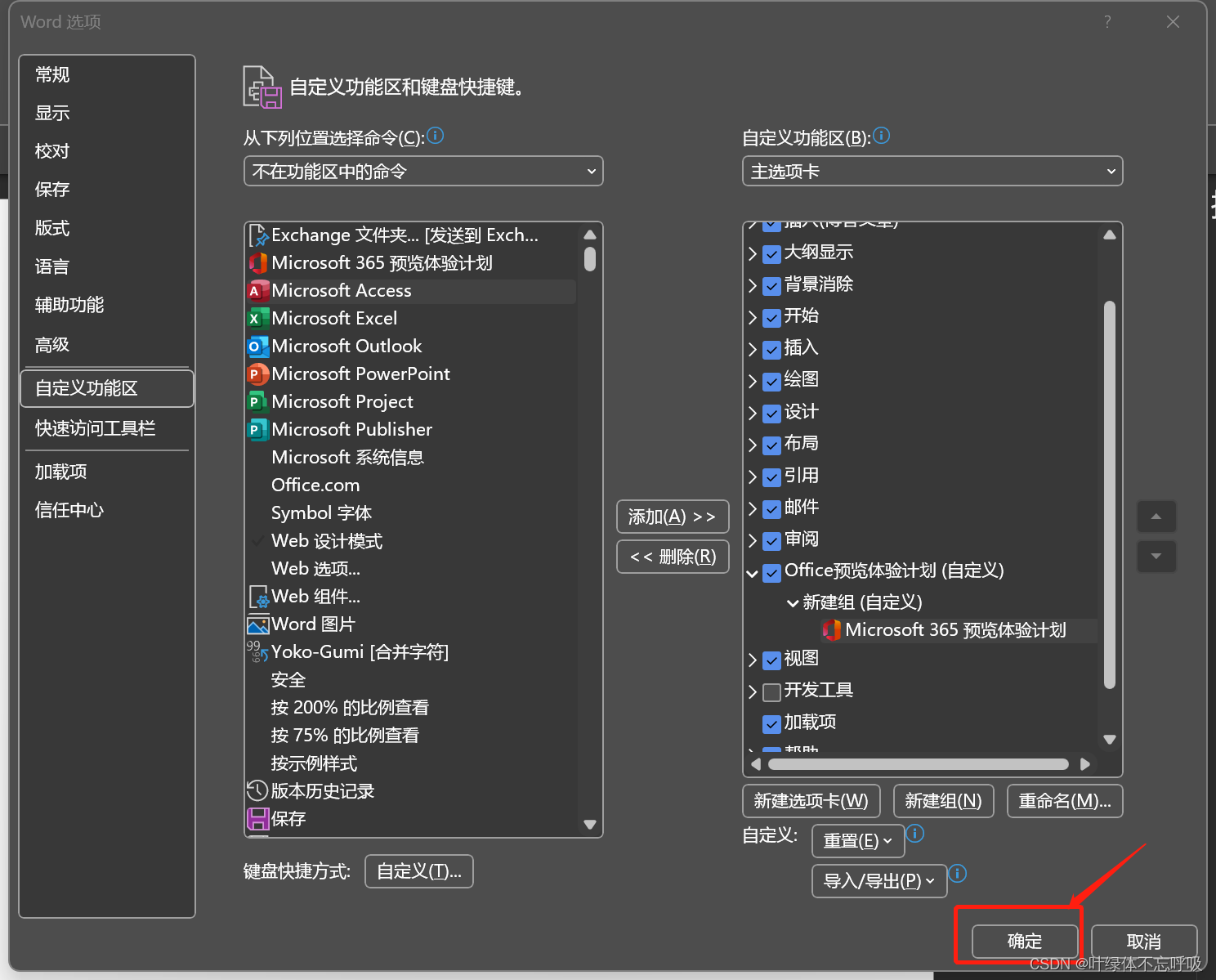
我们就可以在word首页看到刚刚设置的: ofice预览体验计划这个选项卡了
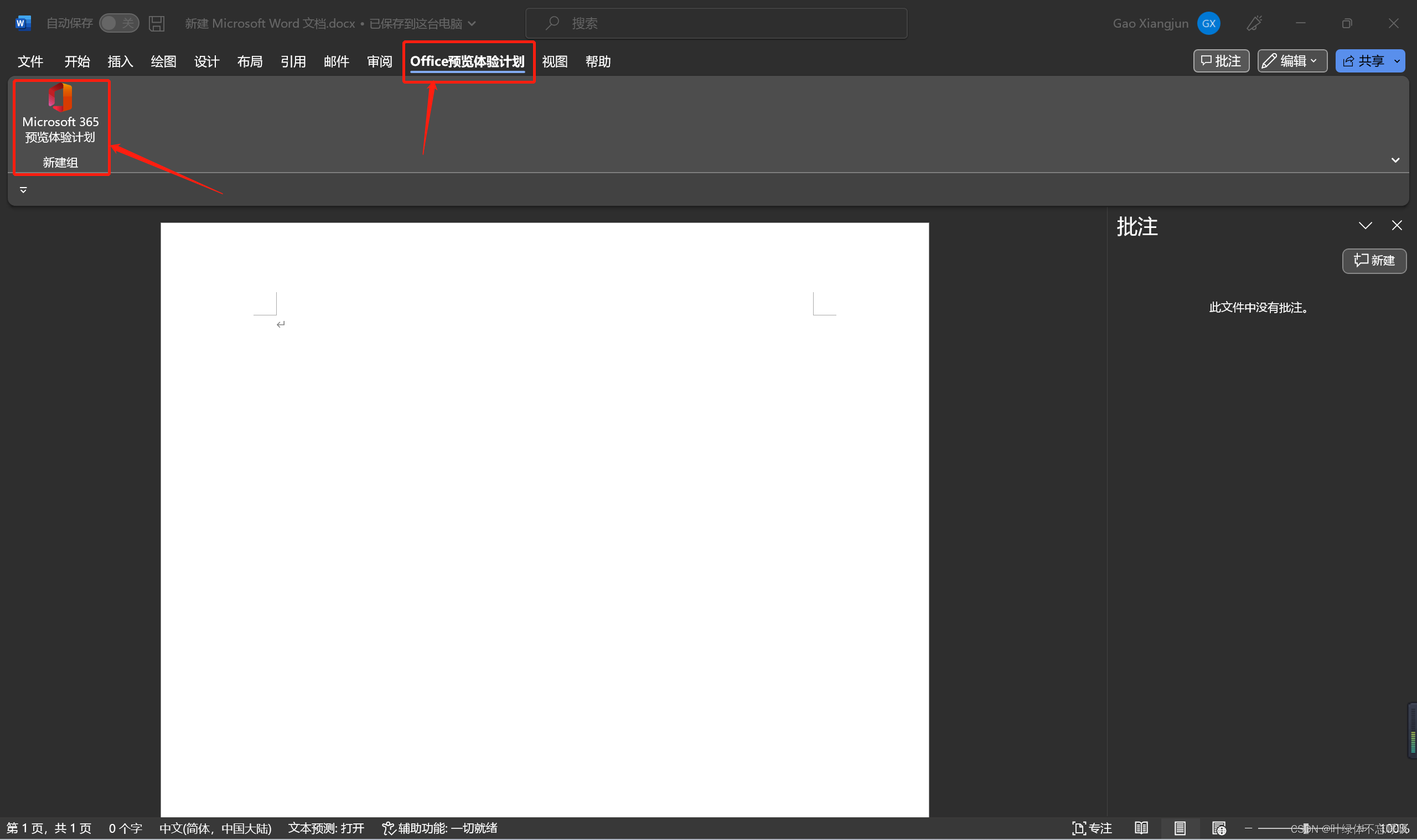
点击我们自己添加的“office预览体验计划”,点一下,会弹出一个框
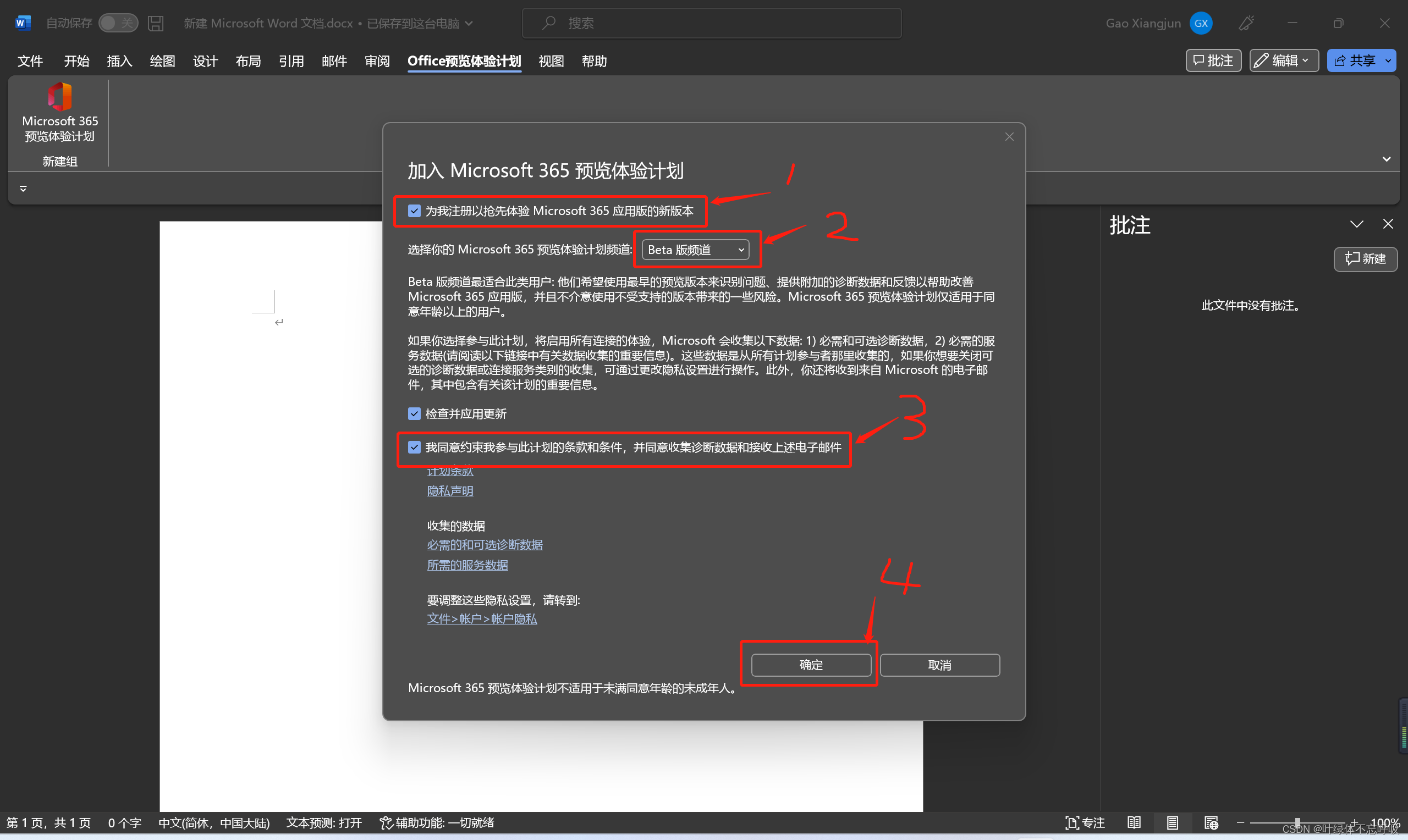
按照这个图操作:
勾选上面的“为我注册以获得提前体验office新版本的资格”然后在下面一行“选择你的ofice预览体验计划频道”右边可看到可选的下拉菜单,在这里选择beta版频道,然后勾选“我同意有关我参与此计划的条款和条件,并且同意收集上述诊断数据”再选择“确定”即可成功加入。
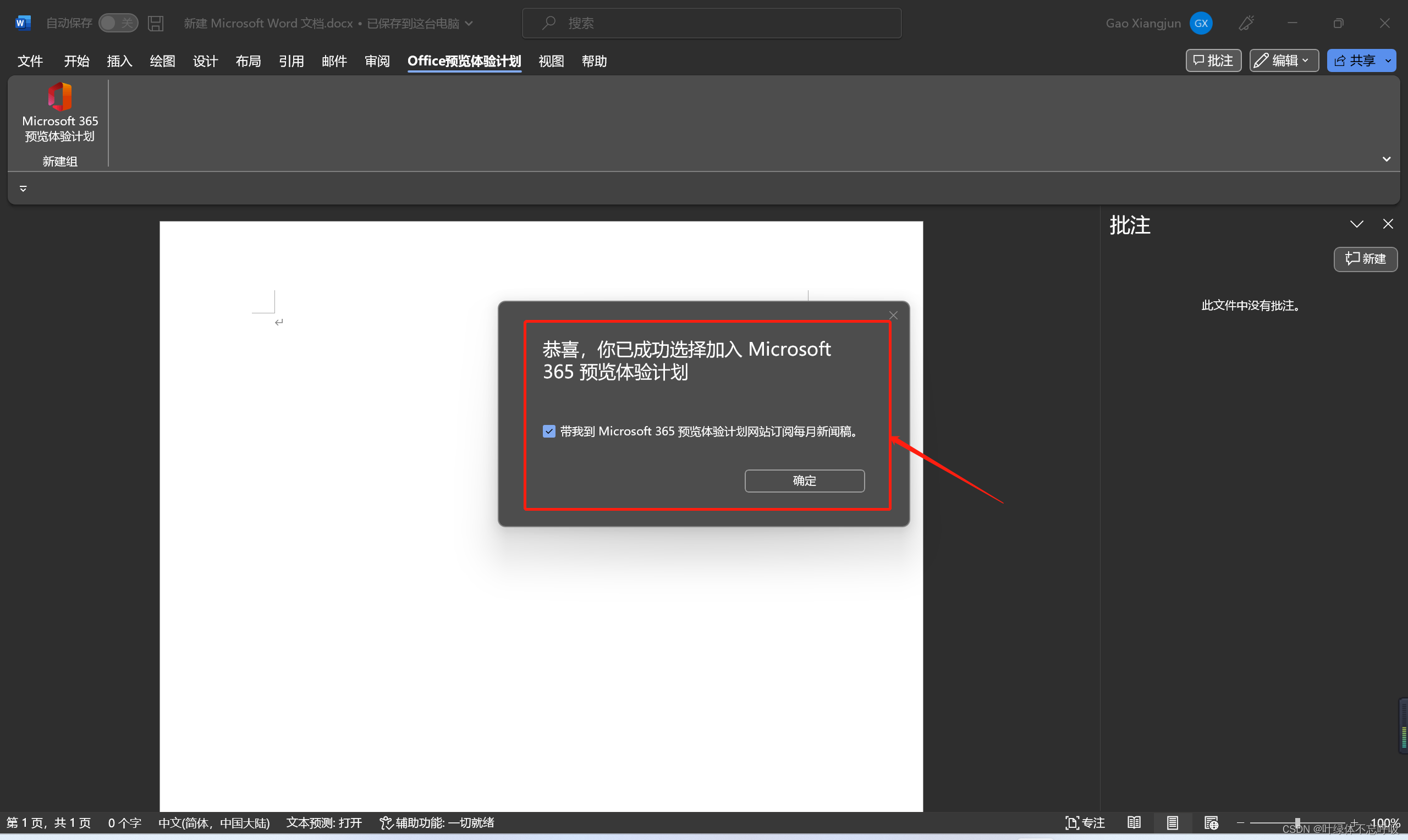
之后office会自动更新,如果没有自动更新,可以在账户-选项里,选择“Office 更新”旁边的下拉菜单中的“立即更新”ofice将在后台自动更新。
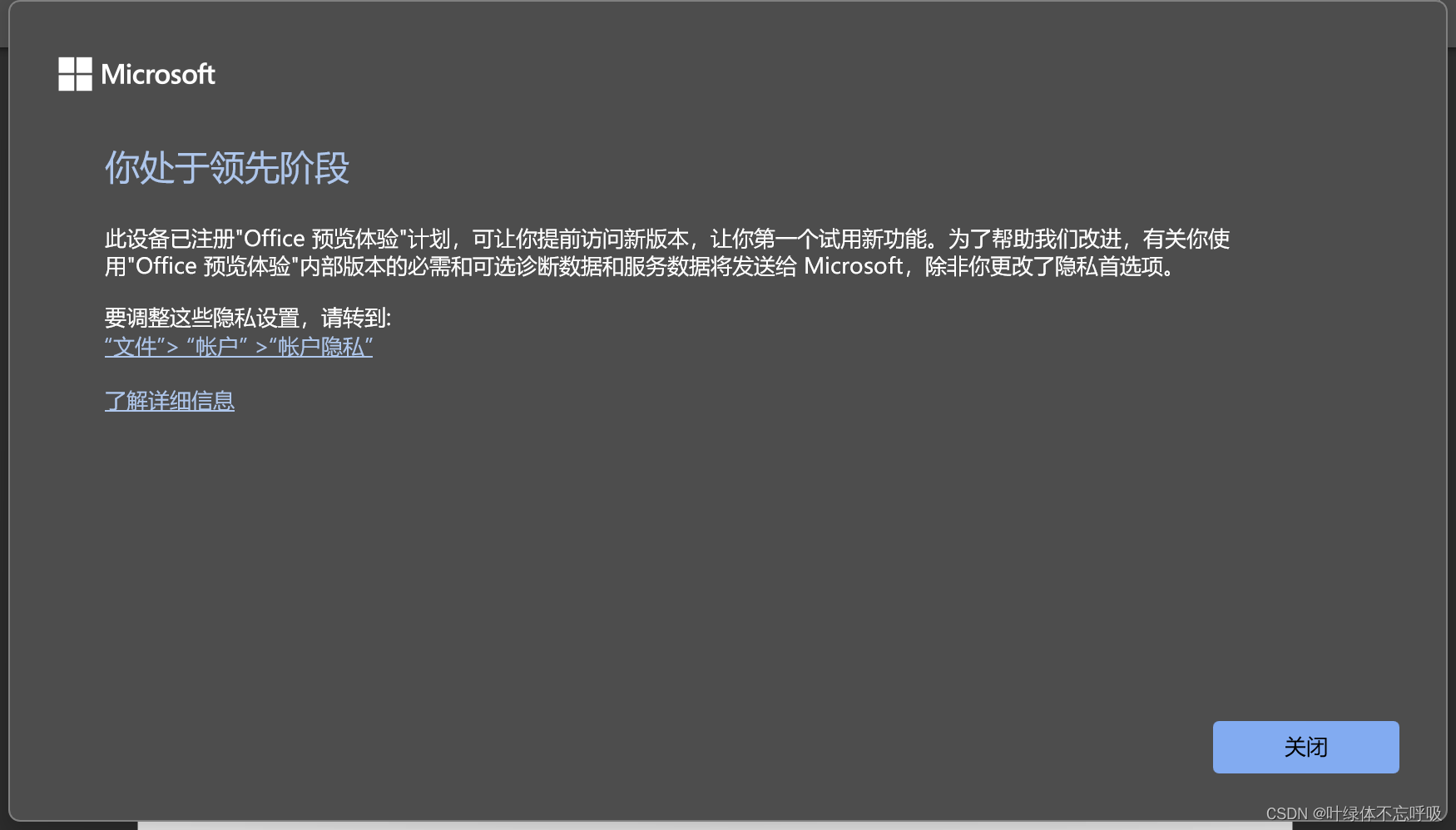
更新完成后会有这个弹框,如果不确定自己是否是最新的版本,也可以在自己账户页面,点击“更新选项”按钮,它会告诉你当前是否是最新版本。
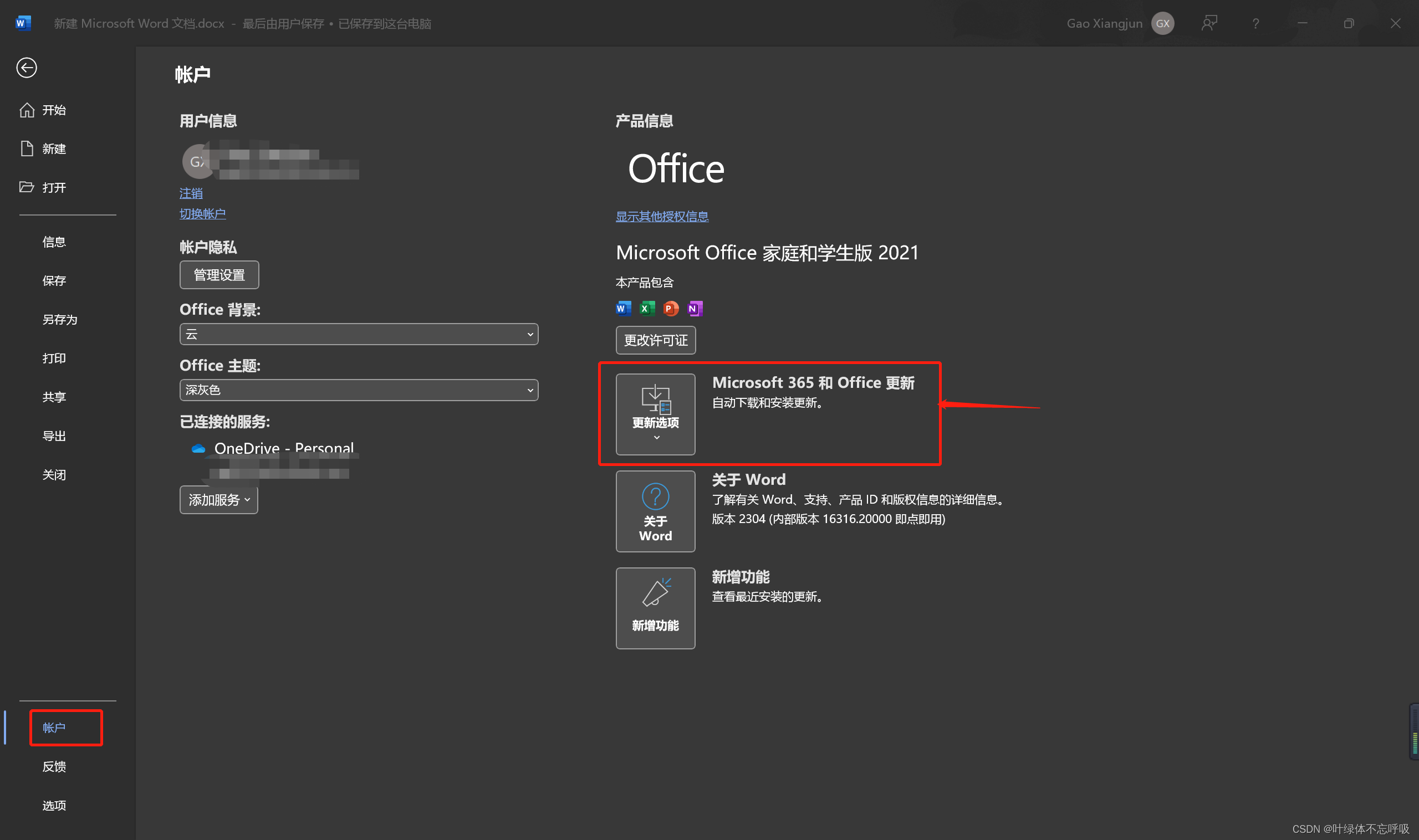
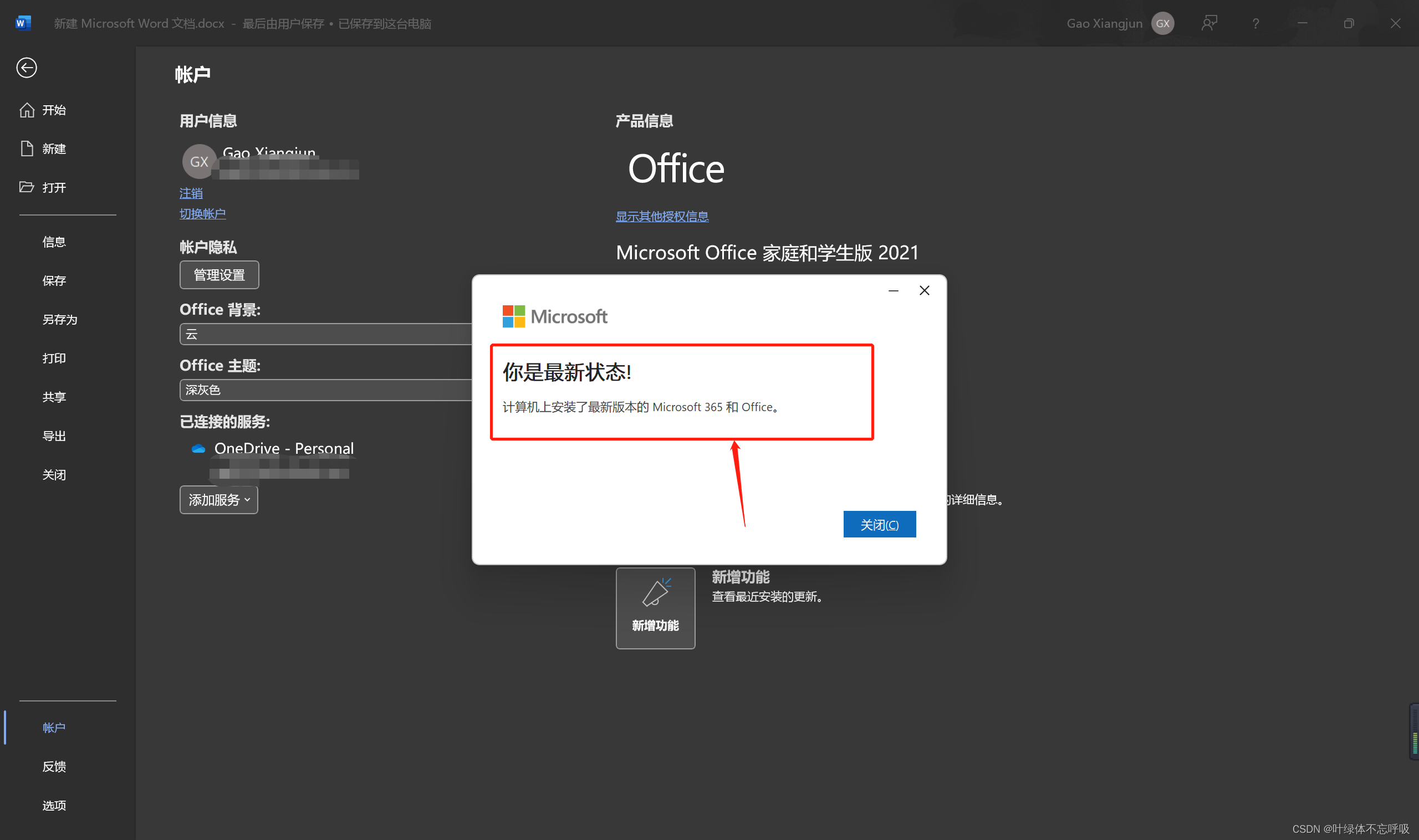
当安装更新完后,会有这样子的弹框
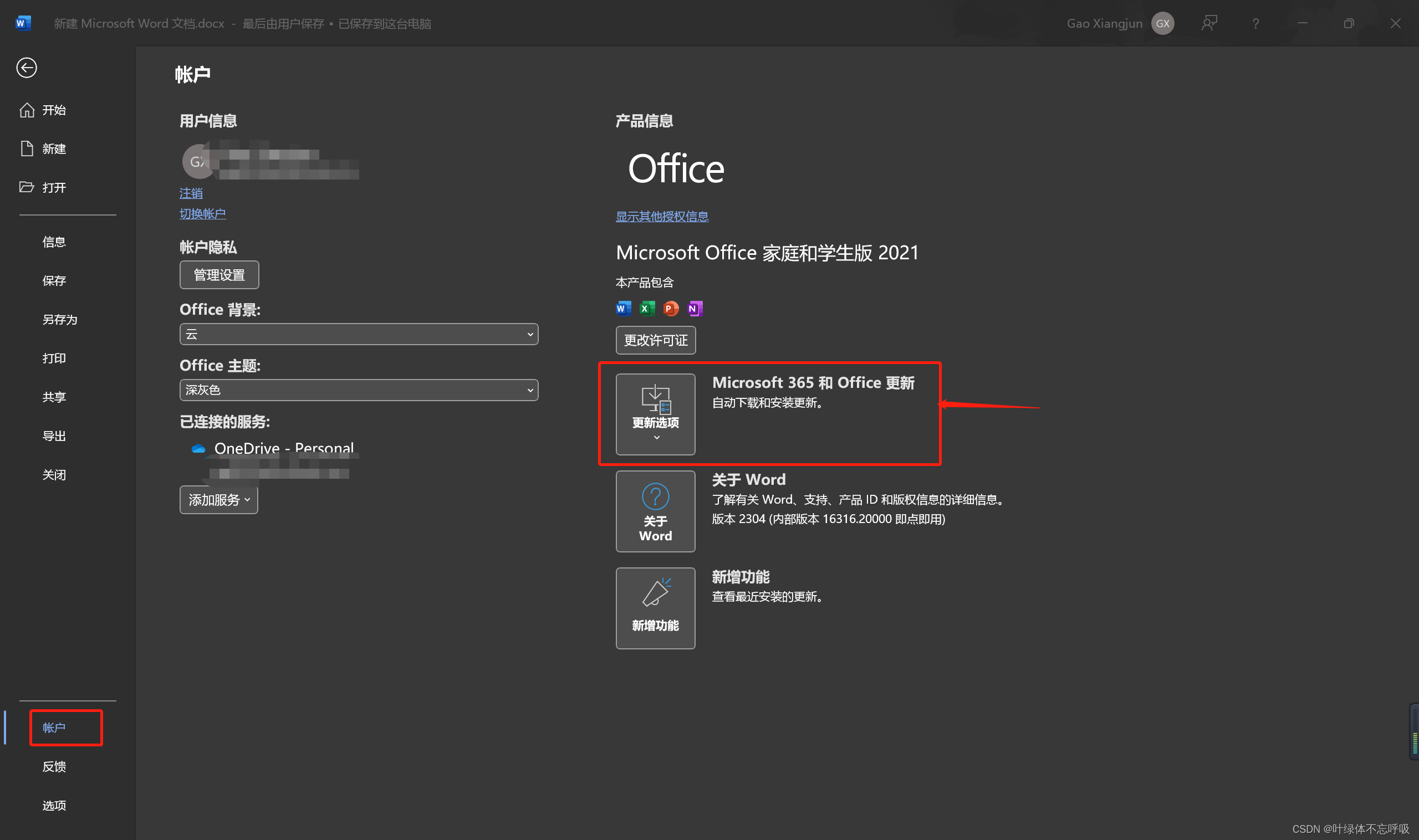
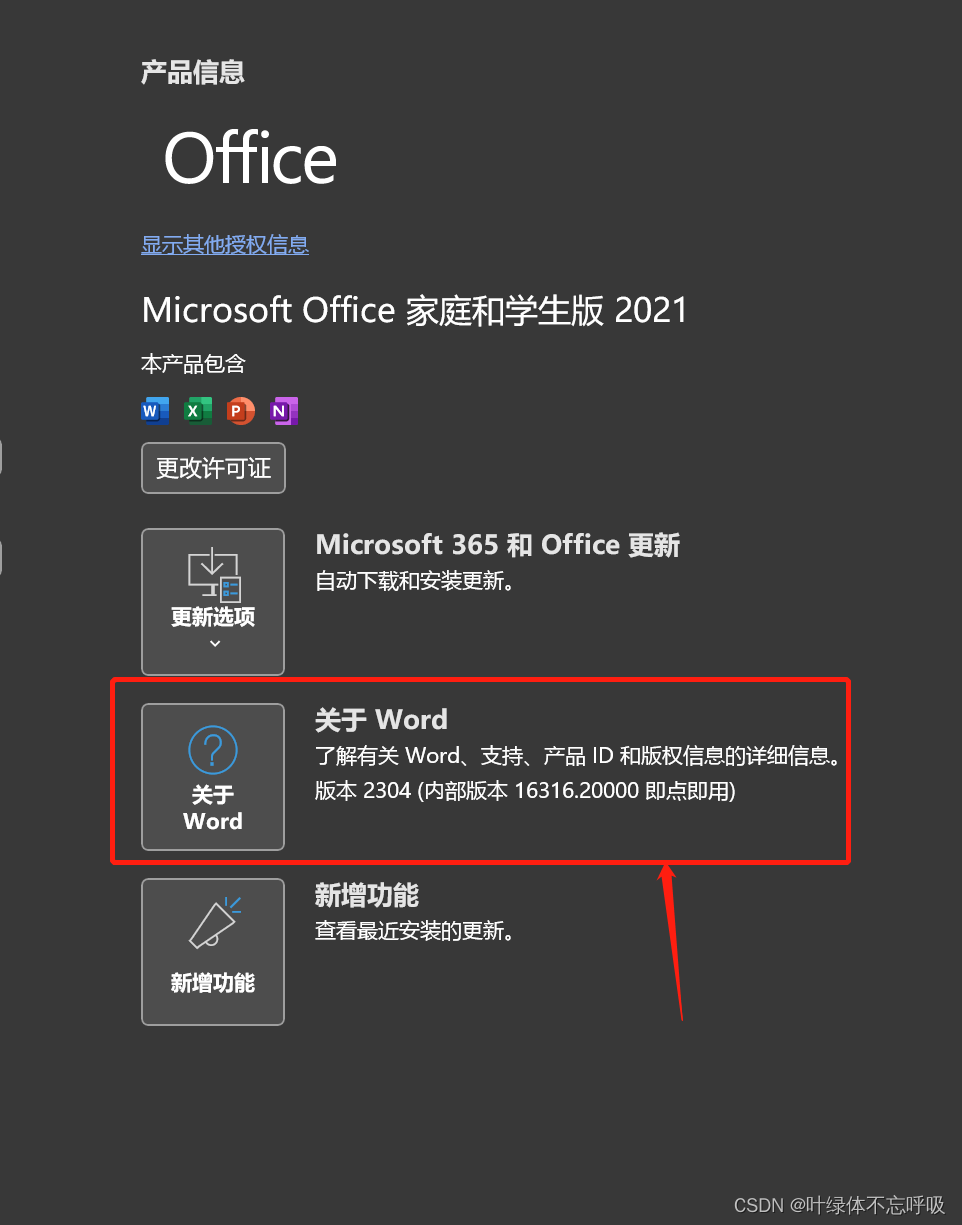
点击这个“关于”,可以查看当前版本
关闭word,重新打开,会看到自己账户页面多了一个信息
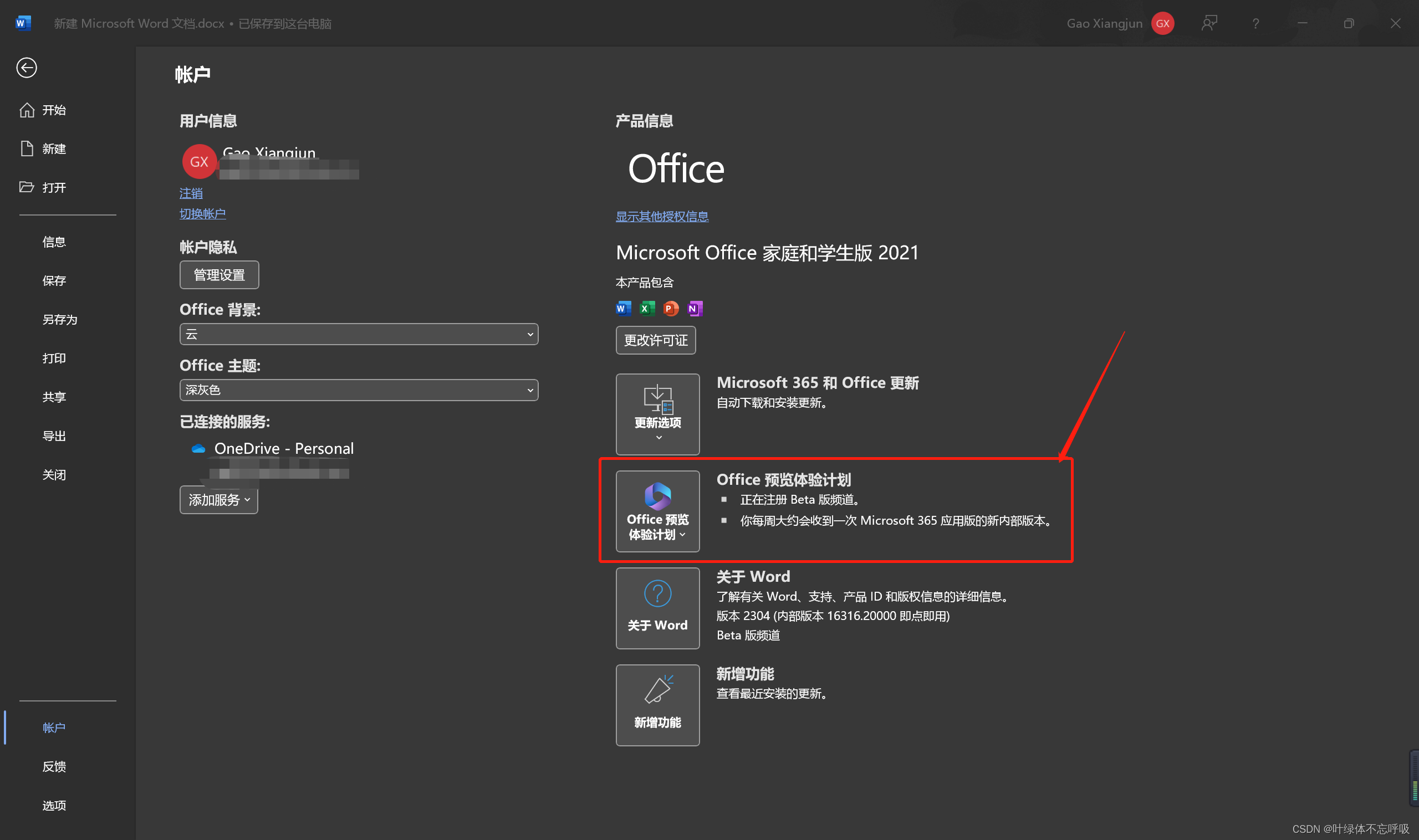
如果没有出来这个,可能需要你重启下电脑
到目前为止,我们已经申请加入ofice预览体验计划了,要做的就是等待审批通过即可,这个审批通过是随机的。






)


函数)
(12))


)


)



