🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

📌树的定义
树(Tree)是n(n≥0)个结点的有限集.n=0时称为空树.
在任意一颗非空树中:
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集
,其中每一个集合本身又是一颗树,并且称为根的子树(SubTree),如下图:
有关树的定义我们还需强调两点:
- n>0时根节点是唯一的,不可能存在多个根节点.
- m>0时,子树的个数没有限制,但它们一定是互不相交的.下图的两个结构就不符合树的定义,因为它们都有相交的子树:
📌树的相关概念

- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6.
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I、K、L、...等节点为叶节点.
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G、J等节点为分支节点.
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点.
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点.
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点.
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6.
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4.
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点.
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先.
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙.
- 森林:由m(m>0)棵互不相交的树的集合称为森林.
📌线性结构与树结构的对比
线性结构
- 第一个数据元素:无前驱
- 最后一个数据元素:无后继
- 中间元素:一个前驱一个后继
树结构
- 根节点:无双亲且唯一
- 叶节点:无孩子,可以存在多个
- 中间节点:一个双亲多个孩子
📌树的抽象数据类型
这里我们给出了一些树的基本常用操作:
ADT 树(tree)
Data树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
OperationInitTree(*T):构造空树T。DestroyTree(*T):销毁树T。CreateTree(*T,definition):按definition中给出树的定义来构造树。ClearTree(*T):若树T存在,则将树T清为空树。TreeEmpty(*T):若树T为空树,返回true,否则返回false。TreeDepth(*T):返回树T的深度。Root(T):返回T的根结点。Value(T,cur_e):cur_e是树T中一个结点,返回此结点的值。Assign(T,cur_e,value):给树T的结点cur_e赋值为value。Parent(T,cur_e):若cur_e是树T中的非根结点,则返回它的双亲,否则返回空。LeftChild(T,cur_e):若cur_e是树T的非叶结点,则返回它的最左孩子,否则返回空。RightSibling(T,cur_e):若cur_e有右兄弟,则返回它的右兄弟,否则返回空。InsertChild(*T,*p,i,c):其中p指向树T的某个结点,i为所指结点p的度加上1,非空树c与T不相交,操作结果为插入c为树T中p指结点的第i棵子树。DeleteChild(*T,*p,i): 其中p指向树T的某个结点, i为所指结点p的度,操作结果为删除T中p所指结点的第i棵子树。
endADT📌树的存储结构
对于树的存储结构,我们这里介绍三种不同的表示法:双亲表示法、孩子表示法、孩子兄弟表示法。
🎏双亲表示法
在链表中,我们设置的结点结构是由一个数据域和一个指针域构成的,如下图:

而到了树结构中,由于树中包含了诸多重要的要素,我们的结点构成就非常的灵活了,以双亲表示法为例,我们在每个结点中,附设一个指示器指示其双亲结点在数组的位置.也就是说,每个节点除了知道自己是谁外,还知道它的双亲在哪里.它的结点结构如下图所示:

🎏孩子表示法
孩子表示法的思路是:
把每个结点放到一个顺序存储结构的数组里,再对每个结点的孩子建立一个单链表体现它们的关系.
具体办法是:
把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空.然后n个头指针又组成一个线性表,采用顺序存储结构,放进一个一维数组中,如下图所示:

🎏孩子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的.因此,我们设置两个指针,分别指向该结点的第一个孩子和此节点的右兄弟.
结点示意图:
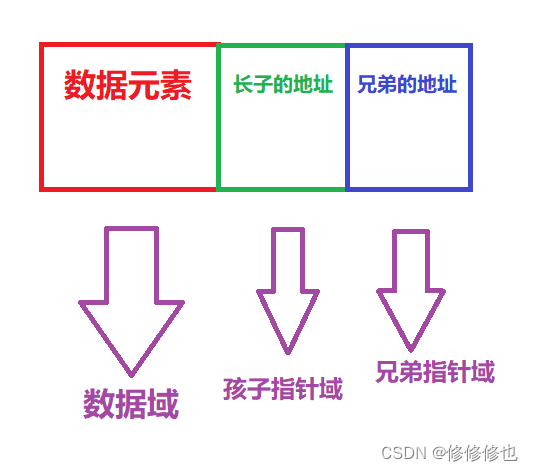
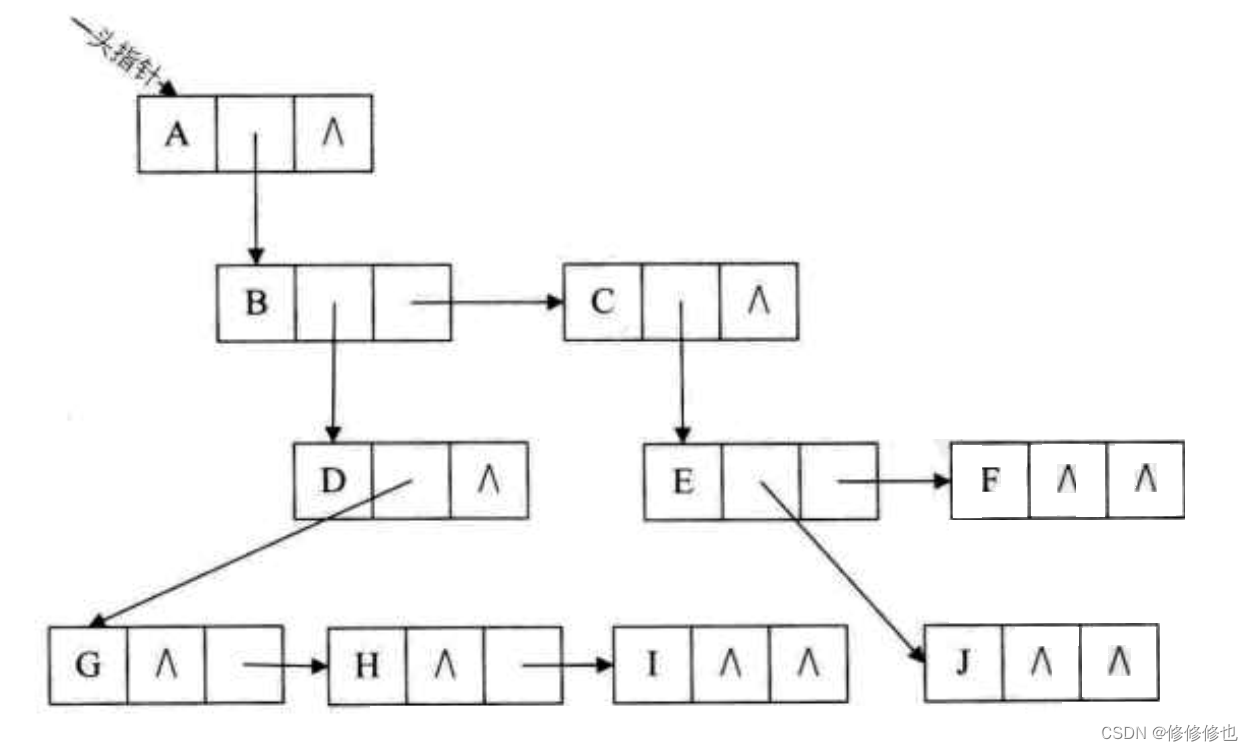
该方法实现的树如下图所示:
结语
希望这篇树的介绍能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是线性表?
【数据结构】线性表的链式存储结构
【数据结构】什么是栈?
【数据结构】用C语言实现顺序栈(附完整运行代码)
【数据结构】深入浅出理解链表中二级指针的应用
【数据结构】10道经典面试题目带你玩转链表











——二叉树)





:对象的重要特性:构造函数与析构函数)





