算法提高课整理

CSDN个人主页：更好的阅读体验

原题链接

题目描述

给定一个长度为 $n$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 $k$ 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式

第一行包含整数 $n,k$，表示数组的长度以及你可以完成的最大交易笔数。

第二行包含 $n$ 个不超过 $10^4$ 的正整数，表示完整的数组。

输出格式

输出一个整数，表示最大利润。

数据范围

$1\le N\le 10^5$,
$1\le k\le 100$

---

思路

本题为 DP 问题，可以使用 闫氏DP分析法 解题。

DP：

• 状态表示 $f_{i,j,0/1}$：
  • 集合：在前 $i$ 天中进行买卖，第 $i$ 天【持有 $(1)$ | 不持有 $(0)$】股票且已经完成 $j$ 笔完整的交易（先卖出后买入）的所有方案的集合。
  • 属性：$\max$
• 状态计算：
  • 本题状态较复杂，如何用 $0/1$ 表示各种状态转移？
    • $0\to 0$ 继续不持有股票；
    • $0\to 1$ 买当天的股票；
    • $1\to 0$ 卖出手里的股票；
    • $1\to 1$ 继续持有股票。
  • 解决了状态转移的问题，考虑设计状态转移方程。
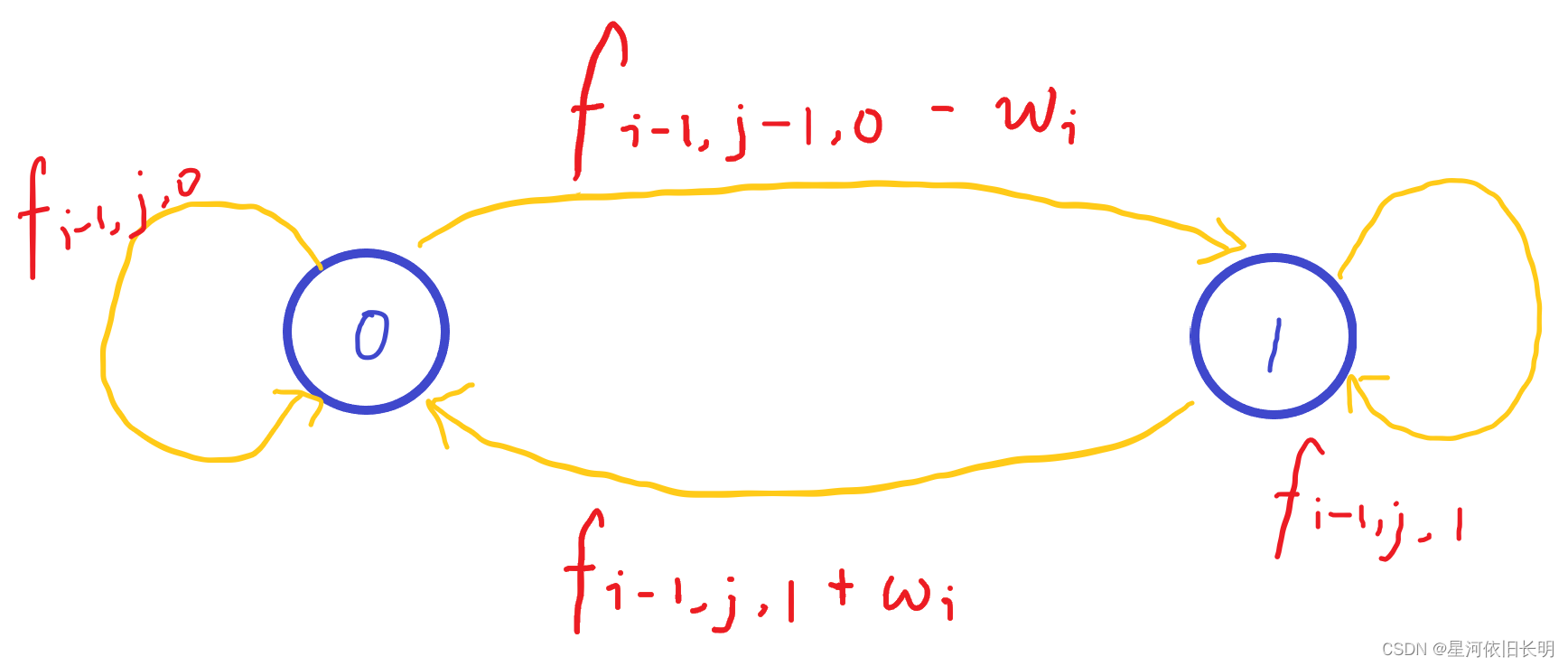
  • 观察下图状态机，我们发现：
    • $f_{i,j,0}$ 由上一层的两个状态 $f_{i-1,j,0},f_{i-1,j,1}$ 转移过来，因此状态转移方程为：f[j][0] = max(f[j][0], f[j][1] + w[i]);
    • $f_{i,j,1}$ 由上一层的两个状态 $f_{i-1,j,1},f_{i-1,j-1,0}$ 转移过来，因此状态转移方程为：f[j][1] = max(f[j][1], f[j - 1][0] - a[i]);

• 初始化

  • 由于有的状态值为负数，对应到实际情况就是亏钱的股票买卖，所以我们即使求最大值也应该将所有状态都初始化为 $-\infty$。
  • f[0][0][0] = 0; 什么都没有，当然是 $0$ 咯~

• 目标状态：$f_{n,0\sim k,0}$（即所有日期都考虑了，买卖次数不超过 $k$ 次，最后手里不剩股票的所有状态）。

---

疑难解答

Q：为什么状态的设计是先卖出再买入呢？题中不是先买入嘛？

A：第一支股票第一次操作只有买或不买，一定不可能是卖或不卖，因此第一支股票买入时必须按照一次交易处理。

---

算法

时间复杂度 $O(nk)$，空间复杂度 $O(nk)$。

发现空间卡的很紧，容易 MLE。

注意到每次转移全部用的上一层的状态，因此我们考虑滚动数组优化，直接删掉 $f$ 数组的第一维，还是正确的。

AC Code

$\text{C}++$

#include <iostream>
#include <cstring>using namespace std;const int N = 100010, M = 110;int n, m;
int a[N];
int f[M][2]; // 滚动数组int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ )scanf("%d", &a[i]);memset(f, -0x3f, sizeof f);f[0][0] = 0; // 初始化for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ ){f[j][0] = max(f[j][0], f[j][1] + a[i]);f[j][1] = max(f[j][1], f[j - 1][0] - a[i]);}int res = 0;for (int i = 0; i <= m; i ++ )res = max(res, f[i][0]);printf("%d\n", res);return 0;
}

---

最后，如果觉得对您有帮助的话，点个赞再走吧！