概述
研一时为应付高等工程数学考试整理的有关数值分析部分的内容,目的是为了应付考试。
误差
误差限与有效数字的联系
对于有 n n n 位有效数字的 x x x 的近似值 x ∗ x^* x∗, 其科学计数法表示形式 x ∗ = a 1 . a 2 . . . a n × 1 0 m ( a 1 ≠ 0 ) x^* = a_1.a_2...a_n\times 10^m \ \ (a_1 \ne 0) x∗=a1.a2...an×10m (a1=0)
绝对误差限 : ∣ e ∣ = ∣ x ∗ − x ∣ ≤ 1 2 ∗ 1 0 m + 1 − n 相对误差限 : ∣ e r ∣ = ∣ x ∗ − x ∣ ∣ x ∣ ≈ ∣ x ∗ − x ∣ ∣ x ∗ ∣ ≤ 1 2 ∗ a 1 ∗ 1 0 1 − n \begin{array} {ll} 绝对误差限 &:& |e| &=& |x^*-x| &\le& \frac{1}{2} * 10^{m+1-n} \\ \\ 相对误差限 &:& |e_r| &=& \frac{|x^*-x|}{|x|} \approx \frac{|x^*-x|}{|x^*|} &\le& \frac{1}{2*a_1} * 10^{1-n} \end{array} 绝对误差限相对误差限::∣e∣∣er∣==∣x∗−x∣∣x∣∣x∗−x∣≈∣x∗∣∣x∗−x∣≤≤21∗10m+1−n2∗a11∗101−n
函数逼近与曲线拟合
函数内积
-
连续型
( f , g ) = ∫ a b ρ ( x ) × f ( x ) × g ( x ) d x (f,g)=\int_a^b \rho(x)\times f(x) \times g(x) dx (f,g)=∫abρ(x)×f(x)×g(x)dx -
离散型
x x x x 0 x_0 x0 x 1 x_1 x1 x 2 x_2 x2 x 3 x_3 x3 f ( x ) f(x) f(x) f ( x 0 ) f(x_0) f(x0) f ( x 1 ) f(x_1) f(x1) f ( x 2 ) f(x_2) f(x2) f ( x 3 ) f(x_3) f(x3) g ( x ) g(x) g(x) g ( x 0 ) g(x_0) g(x0) g ( x 1 ) g(x_1) g(x1) g ( x 2 ) g(x_2) g(x2) g ( x 3 ) g(x_3) g(x3) ( f , g ) = f T g 向量内积 \begin{array} {ll} (f,g) &=& f^Tg &向量内积 \\ \end{array} (f,g)=fTg向量内积
线性无关函数族
- 线性无关的函数族: { 1 , x , x 2 , . . . , x n , . . . } \{1,x,x^2,...,x^n,...\} {1,x,x2,...,xn,...}
- 线性相关的函数族: { 1 , x , 2 x , . . . , n x , . . . } \{1,x,2x,...,nx,...\} {1,x,2x,...,nx,...}
法方程组
G n ⋅ A = D G_n \cdot A = D Gn⋅A=D
其中: G n = [ ( φ 0 , φ 0 ) ( φ 0 , φ 1 ) ⋯ ( φ 0 , φ n ) ( φ 1 , φ 0 ) ( φ 1 , φ 1 ) ⋯ ( φ 1 , φ n ) ⋮ ⋮ ⋮ ( φ n , φ 0 ) ( φ n , φ 1 ) ⋯ ( φ n , φ n ) ] n + 1 A = [ a 0 a 1 . . . a n ] D = [ ( φ 0 , f ) ( φ 1 , f ) . . . ( φ n , f ) ] G_n=\left[\begin{array}{cccc} \left(\varphi_0, \varphi_0\right) & \left(\varphi_0, \varphi_1\right) & \cdots & \left(\varphi_0, \varphi_n\right) \\ \left(\varphi_1, \varphi_0\right) & \left(\varphi_1, \varphi_1\right) & \cdots & \left(\varphi_1, \varphi_n\right) \\ \vdots & \vdots & & \vdots \\ \left(\varphi_n, \varphi_0\right) & \left(\varphi_n, \varphi_1\right) & \cdots & \left(\varphi_n, \varphi_n\right) \end{array}\right]_{n+1} \ \ A = \left[\begin{array}{lll} a_0 \\ a_1 \\... \\ a_n \end{array} \right] \ \ \ D= \left[\begin{array}{lll} (\varphi_0, f) \\ (\varphi_1,f) \\... \\ (\varphi_n, f) \end{array} \right] Gn= (φ0,φ0)(φ1,φ0)⋮(φn,φ0)(φ0,φ1)(φ1,φ1)⋮(φn,φ1)⋯⋯⋯(φ0,φn)(φ1,φn)⋮(φn,φn) n+1 A= a0a1...an D= (φ0,f)(φ1,f)...(φn,f)
正交函数族
- 三角函数族 { 1 , c o s x , s i n x , c o s ( 2 x ) , s i n ( 2 x ) , . . . } \{1, cosx, sinx, cos(2x), sin(2x), ...\} {1,cosx,sinx,cos(2x),sin(2x),...}
- Legendre(勒让德)多项式 { 1 , x , 1 2 ( 3 x 2 − 1 ) , 1 2 ( 5 x 3 − 3 x ) , 1 8 ( 35 x 4 − 30 x 2 + 3 ) . . . } \{1, x, \frac{1}{2}(3x^2-1), \frac{1}{2}(5x^3-3x), \frac{1}{8}(35x^4-30x^2+3)...\} {1,x,21(3x2−1),21(5x3−3x),81(35x4−30x2+3)...}
- Chebyshev(切比雪夫)多项式 { 1 , x , 2 x 2 − 1 , 4 x 3 − 3 x , 8 x 4 − 8 x 2 + 1... , c o s ( n × a r c c o s ( x ) ) } \{1,x,2x^2-1,4x^3-3x,8x^4-8x^2+1...,cos(n\times arccos(x)) \} {1,x,2x2−1,4x3−3x,8x4−8x2+1...,cos(n×arccos(x))}
多项式的正交化算法
正交多项式递推公式
g k + 1 ( x ) = ( x − α k ) × g k ( x ) − β k × g k − 1 ( x ) , k = 0 , 1 , 2 , ⋯ g _ { k + 1 } ( x ) = ( x - \alpha _ { k } ) \times g _ { k } ( x ) - \beta _ k \times g_{ k - 1 } ( x ) , \quad k = 0, 1 , 2 , \cdots gk+1(x)=(x−αk)×gk(x)−βk×gk−1(x),k=0,1,2,⋯
其中:
{ α k = ( x × g k , g k ) ( g k , g k ) β k = ( g k , g k ) ( g k − 1 , g k − 1 ) β 0 = 0 g 0 ( x ) = 1 \left\{ \begin{array} {ll} \alpha_k &=& \frac{ ( x \times g_k , g_k ) } { ( g_{ k }, g_{k} ) } \\ \beta_k &=& \frac { ( g_k , g_k ) } { ( g_{ k-1 } , g_{ k-1 } ) } \\ \beta_0 &=& 0 \\ g_0(x) &=& 1 \end{array} \right. ⎩ ⎨ ⎧αkβkβ0g0(x)====(gk,gk)(x×gk,gk)(gk−1,gk−1)(gk,gk)01
算法流程
- 由 g k ( x ) g_k(x) gk(x) 计算出 α k , β k \alpha_k, \beta_k αk,βk
- 由 g k − 1 ( x ) , g k ( x ) g_{k-1}(x), g_{k}(x) gk−1(x),gk(x) 通过递推公式得到 g k + 1 ( x ) g_{k+1}(x) gk+1(x)
法方程组
G n ⋅ A = D G_n \cdot A = D Gn⋅A=D
其中: G n = [ ( g 0 , g 0 ) 0 ⋯ 0 0 ( g 1 , g 1 ) ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ ( g n , g n ) ] n + 1 A = [ a 0 a 1 . . . a n ] D = [ ( g 0 , f ) ( g 1 , f ) . . . ( g n , f ) ] G_n=\left[\begin{array}{cccc} (g_0, g_0) & 0 & \cdots & 0 \\ 0& (g_1, g_1) & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & (g_n, g_n) \end{array}\right]_{n+1} \ \ A = \left[\begin{array}{lll} a_0 \\ a_1 \\... \\ a_n \end{array} \right] \ \ \ D= \left[\begin{array}{lll} (g_0, f) \\ (g_1,f) \\... \\ (g_n, f) \end{array} \right] Gn= (g0,g0)0⋮00(g1,g1)⋮0⋯⋯⋯00⋮(gn,gn) n+1 A= a0a1...an D= (g0,f)(g1,f)...(gn,f)
故可以直接解出 a k = ( g k , f ) ( g k , g k ) a_k = \frac{(g_k, f)}{(g_k, g_k)} ak=(gk,gk)(gk,f)
常用的正交多项式(一): Legendre多项式
定义
积分区间在 [ − 1 , 1 ] [-1,1] [−1,1], 权函数 ρ ( x ) = 1 \rho(x)=1 ρ(x)=1, 由 g 1 ( x ) = x g_1(x)=x g1(x)=x 正交化得到的多项式称为 Legendre多项式
区间变换公式
将积分区间由 x ∈ [ a , b ] x \in [a,b] x∈[a,b] 转变为 t ∈ [ − 1 , 1 ] t \in [-1, 1] t∈[−1,1]
x = b − a 2 × t + b + a 2 x = \frac{b-a}{2} \times t + \frac{b+a}{2} x=2b−a×t+2b+a
通项公式
一般使用 P n ( x ) P_n(x) Pn(x) 替换 φ n ( x ) \varphi_n(x) φn(x) 来表示Legendre多项式
P n ( x ) = 1 2 n × n ! d n d x n ( x 2 − 1 ) n P_n(x) = \frac{1}{2^n \times n!} \frac{d^n}{dx^n}(x^2-1)^n Pn(x)=2n×n!1dxndn(x2−1)n
| 阶数 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Legendre多项式 | 1 | x x x | 1 2 ( 3 x 2 − 1 ) \frac{1}{2}(3x^2-1) 21(3x2−1) | 1 2 ( 5 x 3 − 3 x ) \frac{1}{2}(5x^3-3x) 21(5x3−3x) | 1 8 ( 35 x 4 − 30 x 2 + 3 ) \frac{1}{8}(35x^4-30x^2+3) 81(35x4−30x2+3) |
性质
-
正交性
( P k , P k ) = ∫ − 1 1 1 × P k ( x ) × P k ( x ) d x = 2 2 k + 1 (P_k, P_k) = \int_{-1}^{1} 1 \times P_k(x) \times P_k(x) dx = \frac{2}{2 k + 1} (Pk,Pk)=∫−111×Pk(x)×Pk(x)dx=2k+12 -
Legendre多项式的递推公式
( n + 1 ) × P n + 1 ( x ) = ( 2 n + 1 ) × x × P n ( x ) − n × P n − 1 ( x ) (n+1) \times P_{n+1}(x) = (2n+1) \times x \times P_n(x) - n \times P_{n-1}(x) (n+1)×Pn+1(x)=(2n+1)×x×Pn(x)−n×Pn−1(x)
常用的正交多项式(二): Chebyshev多项式
定义
积分区间在 [ − 1 , 1 ] [-1,1] [−1,1], 权函数 ρ ( x ) = 1 1 − x 2 \rho(x) = \frac{1}{\sqrt{1-x^2}} ρ(x)=1−x21, 由 g 1 ( x ) = x g_1(x)=x g1(x)=x 正交化得到的正交多项式称为 Chebyshev多项式
通项公式
一般使用 T n ( x ) T_n(x) Tn(x) 替换 φ n ( x ) \varphi_n(x) φn(x) 来表示Chebyshev多项式
T n ( x ) = c o s ( n × a r c c o s ( x ) ) T_n(x) = cos(n \times arccos(x)) Tn(x)=cos(n×arccos(x))
| 阶数 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Chebyshev多项式 | 1 | x x x | 2 x 2 − 1 2x^2-1 2x2−1 | 4 x 3 − 3 x 4x^3-3x 4x3−3x | 8 x 4 − 8 x 2 + 1 8x^4-8x^2+1 8x4−8x2+1 |
性质
-
正交性
( T k , T k ) = { π 2 , k = 0 π , k ≠ 0 (T_k, T_k) = \left\{ \begin{array} {ll} \frac{\pi}{2} &,k=0 \\ \pi &,k\ne 0 \\ \end{array} \right. (Tk,Tk)={2ππ,k=0,k=0 -
T n ( x ) = 0 T_n(x) = 0 Tn(x)=0 的解
x k = c o s ( 2 k − 1 2 n π ) x_k = cos(\frac{2k-1}{2n}\pi) xk=cos(2n2k−1π)
最佳平方逼近及其误差(连续函数)
n n n 次最佳平方逼近
使用 n n n 次正交函数族来拟合给定函数
平方误差
记 f ( x ) f(x) f(x) 是待拟合的函数, s ( x ) = ∑ k = 0 n ( a k × P k ( x ) ) s(x) = \sum_{k=0}^n(a_k \times P_k(x)) s(x)=∑k=0n(ak×Pk(x)) 是用来拟合的多项式
∣ ∣ δ ∣ ∣ 2 2 = ∣ ∣ f ( x ) − s ( x ) ∣ ∣ 2 2 = ( f − s , f − s ) = ( f − s , f ) − ( f − s , s ) = ( f − s , f ) = ( f , f ) − ( s , f ) = ( f , f ) − ( f , ∑ k = 0 n ( a k × g k ) ) = ( f , f ) − ∑ k = 0 n a k × ( f , g k ) = ( f , f ) − ∑ k = 0 n a k × a k × ( g k , g k ) \begin{array} {ll} ||\delta||_2^2 = ||f(x)-s(x)||_2^2 &=& (f-s, f-s) \\ \\ &=& (f-s, f) - (f-s, s) \\ \\ &=& (f-s,f) \\ \\ &=& (f,f) - (s,f) \\ \\ &=& (f,f) - (f, \sum_{k=0}^n(a_k \times g_k)) \\ \\ &=& (f,f) - \sum_{k=0}^na_k \times (f, g_k) \\ \\ &=& (f,f) - \sum_{k=0}^na_k \times a_k \times (g_k, g_k) \end{array} ∣∣δ∣∣22=∣∣f(x)−s(x)∣∣22=======(f−s,f−s)(f−s,f)−(f−s,s)(f−s,f)(f,f)−(s,f)(f,f)−(f,∑k=0n(ak×gk))(f,f)−∑k=0nak×(f,gk)(f,f)−∑k=0nak×ak×(gk,gk)
- 在Legendre多项式中, g ( x ) = P ( x ) g(x) = P(x) g(x)=P(x), 故 ( g k , g k ) = ( P k , P k ) = 2 2 k + 1 (g_k, g_k)=(P_k, P_k) = \frac{2}{2k+1} (gk,gk)=(Pk,Pk)=2k+12
- 在Chebyshev多项式中, g ( x ) = T ( x ) g(x) = T(x) g(x)=T(x), 故 ( g k , g k ) = ( T k , T k ) = { π 2 , k = 0 π , k ≠ 0 (g_k, g_k) = (T_k, T_k) = \left\{ \begin{array}{ll}\frac{\pi}{2}&,k=0 \\\pi&,k\ne 0 \\\end{array}\right. (gk,gk)=(Tk,Tk)={2ππ,k=0,k=0
曲线拟合的最小二乘法(离散数据点)
在离散的情况下, 此时无论是Legendre多项式还是Chebyshev多项式, 都不能直接使用正交性的结论, 需要根据离散情况下的内积定义进行计算 ( g k , g k ) (g_k, g_k) (gk,gk)
例题
给定数据表, 计算数据的二次多项式拟合
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x i x_i xi | 0 | 0.25 | 0.5 | 0.75 | 1 |
| y i y_i yi | 0.10 | 0.35 | 0.81 | 1.09 | 1.96 |
| 权函数 w i w_i wi | 1 | 1 | 1 | 1 | 1 |
解析: 多项式的正交化算法
-
算法开始: g 0 ( x ) = 1 g_0(x)=1 g0(x)=1
i 1 2 3 4 5 x i x_i xi 0 0.25 0.5 0.75 1 y i y_i yi 0.10 0.35 0.81 1.09 1.96 权函数 w i w_i wi 1 1 1 1 1 g 0 = 1 g_0=1 g0=1 1 1 1 1 1 -
计算 α k , β k \alpha_k, \beta_k αk,βk, 即 α 0 , β 0 \alpha_0, \beta_0 α0,β0
{ α k = ( x × g k , g k ) ( g k , g k ) β k = ( g k , g k ) ( g k − 1 , g k − 1 ) β 0 = 0 \left\{ \begin{array} {ll} \alpha_k &=& \frac{ ( x \times g_k , g_k ) } { ( g_{ k }, g_{k} ) } \\ \beta_k &=& \frac { ( g_k , g_k ) } { ( g_{ k-1 } , g_{ k-1 } ) } \\ \beta_0 &=& 0 \\ \end{array} \right. ⎩ ⎨ ⎧αkβkβ0===(gk,gk)(x×gk,gk)(gk−1,gk−1)(gk,gk)0
i 1 2 3 4 5 x i x_i xi 0 0.25 0.5 0.75 1 y i y_i yi 0.10 0.35 0.81 1.09 1.96 权函数 w i w_i wi 1 1 1 1 1 g 0 = 1 g_0=1 g0=1 1 1 1 1 1 x × g 0 x\times g_0 x×g0 0 0.25 0.5 0.75 1 得到: α 0 = 0.5 , β 0 = 0 \alpha_0=0.5, \beta_0=0 α0=0.5,β0=0
-
通过正交多项式的递推公式 g k + 1 ( x ) = ( x − α k ) × g k ( x ) − β k × g k − 1 ( x ) g _ { k + 1 } ( x ) = ( x - \alpha _ { k } ) \times g _ { k } ( x ) - \beta _ k \times g_{ k - 1 } ( x ) gk+1(x)=(x−αk)×gk(x)−βk×gk−1(x) 得到 g 1 ( x ) = x − 0.5 g_1(x)=x-0.5 g1(x)=x−0.5, 重复步骤(1)到(3)
i 1 2 3 4 5 x i x_i xi 0 0.25 0.5 0.75 1 y i y_i yi 0.10 0.35 0.81 1.09 1.96 权函数 w i w_i wi 1 1 1 1 1 g 0 = 1 g_0=1 g0=1 1 1 1 1 1 x × g 0 x\times g_0 x×g0 0 0.25 0.5 0.75 1 g 1 = x − 0.5 g_1=x-0.5 g1=x−0.5 -0.5 -0.25 0 0.25 0.5
#插值法
代数插值多项式
基本形式
P n ( x ) = ∑ k = 0 n ( a k × x k ) \begin{array} {ll} P_n(x) = \sum_{k=0}^{n}(a_k \times x^k) \end{array} Pn(x)=∑k=0n(ak×xk)
截断误差公式(余项)
R n ( x ) = f ( n + 1 ) ( ϵ ) ( n + 1 ) ! w n + 1 ( x ) \begin{array} {ll} R _ { n } ( x ) &=& \frac { f ^ { ( n + 1 ) } ( \epsilon ) } { ( n + 1 ) ! } w _ { n + 1 } ( x ) \\ \end{array} Rn(x)=(n+1)!f(n+1)(ϵ)wn+1(x)
其中, w n + 1 ( x ) = ∏ i = 0 n ( x − x i ) w_{n+1}(x) = \prod_{i=0}^{n}(x-x_i) wn+1(x)=∏i=0n(x−xi)
不足
面对给出的 n + 1 n+1 n+1 组数据点
| x x x | x 0 x_0 x0 | x 1 x_1 x1 | … | x n x_n xn |
|---|---|---|---|---|
| y y y | y 0 y_0 y0 | y 1 y_1 y1 | … | y n y_n yn |
如果使用插值多项式的基本形式, 则面临解如下的一个高阶线性方程组 X ⋅ A = Y X \cdot A = Y X⋅A=Y
其中: X = [ 1 x 0 . . . x 0 n 1 x 1 . . . x 1 n . . . 1 x n . . . x n n ] , A = [ a 0 a 1 . . . a n ] , Y = [ y 0 y 1 . . . y n ] X = \left[\begin{array}{lll} 1&x_0&...&x^n_0 \\ 1&x_1&...&x^n_1\\... \\ 1&x_n&...&x^n_n \end{array} \right], \ \ A = \left[\begin{array}{lll} a_0 \\ a_1 \\... \\ a_n \end{array} \right], \ \ Y= \left[\begin{array}{lll} y_0 \\ y_1 \\... \\ y_n \end{array} \right] X= 11...1x0x1xn.........x0nx1nxnn , A= a0a1...an , Y= y0y1...yn
缺点: 对于 n n n 较大的高阶线性方程组, 称为病态方程组. 不适用
Lagrange(拉格朗日)插值
Lagrange插值多项式
P n ( x ) = ∑ k = 0 n ( l k ( x ) × y k ) = ∑ k = 0 n ( l k ( x ) × y ( x k ) ) \begin{array}{ll} P_n(x) &=& \sum_{k=0}^{n}(l_k(x) \times y_k) \\ \\ &=& \sum_{k=0}^{n}(l_k(x) \times y(x_k)) \end{array} Pn(x)==∑k=0n(lk(x)×yk)∑k=0n(lk(x)×y(xk))
由代数多项式基本形式的 直接求解系数 ⇒ \Rightarrow ⇒ Lagrange插值法的 寻找基函数 l k ( x ) l_k(x) lk(x)
将左边点 ( x i , y i ) (x_i, y_i) (xi,yi) 代入到Lagrange插值形式中, 得到基函数 l k ( x ) l_k(x) lk(x) 应该满足如下性质
l i ( x j ) = { 1 , i = j 0 , i ≠ j l_i(x_j)= \left\{ \begin{array}{ll} 1, & i=j \\ 0, & i \neq j \end{array} \right. li(xj)={1,0,i=ji=j
所以有
l i ( x ) = ∏ j = 0 , i ≠ j j = n x − x j x i − x j l_i(x) = \prod_{j=0,i\ne j}^{j=n}\frac{x-x_j}{x_i-x_j} li(x)=j=0,i=j∏j=nxi−xjx−xj
例题
分别使用线性插值和2次插值计算 ln(11.75) 的近似值
| x x x | 10 | 11 | 12 | 13 |
|---|---|---|---|---|
| y = l n ( x ) y=ln(x) y=ln(x) | 2.3026 | 2.3979 | 2.4849 | 2.5649 |
线性插值: 使用两个插值点(最接近待计算的值)
L 1 ( x ) = ( x − x 1 ) ( x 0 − x 1 ) ⋅ y 0 + ( x − x 0 ) ( x 1 − x 0 ) ⋅ y 1 \begin{array}{l} L_1(x) = \frac{(x-x_1)}{(x_0-x_1)} \cdot y_0 + \frac{(x-x_0)}{(x_1-x_0)} \cdot y_1 \end{array} L1(x)=(x0−x1)(x−x1)⋅y0+(x1−x0)(x−x0)⋅y1
2次插值: 使用三个插值点
L 2 ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) ⋅ y 0 + ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) ⋅ y 1 + ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) ⋅ y 2 L_2(x) = \frac{\left(x-x_1\right)\left(x-x_2\right)}{\left(x_0-x_1\right)\left(x_0-x_2\right)} \cdot y_0 + \frac{\left(x-x_0\right)\left(x-x_2\right)}{\left(x_1-x_0\right)\left(x_1-x_2\right)} \cdot y_1 + \frac{\left(x-x_0\right)\left(x-x_1\right)}{\left(x_2-x_0\right)\left(x_2-x_1\right)} \cdot y_2 L2(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)⋅y0+(x1−x0)(x1−x2)(x−x0)(x−x2)⋅y1+(x2−x0)(x2−x1)(x−x0)(x−x1)⋅y2
Newton(牛顿)插值
差商
Newton插值多项式
N ( x ) = a 0 + a 1 ∗ ( x − x 0 ) + a 2 ∗ ( x − x 0 ) ( x − x 1 ) + . . . + a n − 1 ∗ ( x − x 0 ) . . . ( x − x n − 1 ) N(x) = a_0 + a_1 * (x - x_0) + a_2 * (x-x_0)(x-x_1) + ... + a_{n-1}*(x-x_0)...(x-x_{n-1}) N(x)=a0+a1∗(x−x0)+a2∗(x−x0)(x−x1)+...+an−1∗(x−x0)...(x−xn−1)
Newton插值的扩展: Hermite插值多项式
分段插值
对于大区间使用高阶多项式插值会产生Runge(龙格)现象 ⇒ \Rightarrow ⇒ 对多个小区间使用低阶多项式插值
数值积分
用有限的几个点的函数值 f ( x 0 ) , f ( x 1 ) , . . . , f ( x n ) f(x_0), f(x_1), ..., f(x_n) f(x0),f(x1),...,f(xn) 的线性组合来近似某个区间 [ a , b ] [a,b] [a,b] 上的积分
∫ a b f ( x ) d x = ∑ k = 0 n ( A k × f ( x k ) ) \int_a^b f(x) dx = \sum_{k=0}^n (A_k \times f(x_k)) ∫abf(x)dx=k=0∑n(Ak×f(xk))
A k A_k Ak 称为求积系数, x k x_k xk 称为求积点
- 梯形公式 ∫ a b f ( x ) d x = b − a 2 f ( x a ) + b − a 2 f ( x b ) \int_a^b f(x) dx = \frac{b-a}{2}f(x_a) + \frac{b-a}{2}f(x_b) ∫abf(x)dx=2b−af(xa)+2b−af(xb)
- 辛普森公式 ∫ a b f ( x ) d x = b − a 6 f ( x a ) + 4 ( b − a ) 6 f ( x a + x b 2 ) + b − a 6 f ( x b ) \int_a^b f(x) dx = \frac{b-a}{6}f(x_a) + \frac{4(b-a)}{6}f(\frac{x_a + x_b}{2}) + \frac{b-a}{6}f(x_b) ∫abf(x)dx=6b−af(xa)+64(b−a)f(2xa+xb)+6b−af(xb)
代数精度
求积公式是近似方法, 但希望求积公式能够对尽可能多的函数准确成立, 因此提出了代数精度的概念
定理: 在给定区间 [ a , b ] [a,b] [a,b] 上, 对于给定的 n + 1 n+1 n+1 个互不相同的节点, 一定存在求积系数 A 0 , A 1 , . . . A n A_0, A_1,...A_n A0,A1,...An, 使得求积公式至少具有 n n n 次代数精度
插值型求积公式
∫ a b ρ ( x ) × f ( x ) d x ≈ ∫ a b ρ ( x ) × L n ( x ) d x = ∫ a b ρ ( x ) × ∑ k = 0 n ( l k ( x ) × y k ) d x = ∑ k = 0 n ( y k × ∫ a b [ ρ ( x ) × l k ( x ) ] d x ) = ∑ k = 0 n ( f ( x k ) × A k ) \begin{array}{ll} \int_a^b \rho(x) \times f(x) dx \approx \int_a^b \rho(x) \times L_n(x) dx &=& \int_a^b \rho(x) \times \sum_{k=0}^n (l_k(x) \times y_k) dx \\ \\ &=& \sum_{k=0}^n (y_k \times \int_a^b [\rho(x) \times l_k(x)] dx ) \\ \\ &=& \sum_{k=0}^n (f(x_k) \times A_k ) \end{array} ∫abρ(x)×f(x)dx≈∫abρ(x)×Ln(x)dx===∫abρ(x)×∑k=0n(lk(x)×yk)dx∑k=0n(yk×∫ab[ρ(x)×lk(x)]dx)∑k=0n(f(xk)×Ak)
其中: A k = ∫ a b [ ρ ( x ) × l k ( x ) ] d x A_k = \int_a^b[ \rho(x) \times l_k(x) ]dx Ak=∫ab[ρ(x)×lk(x)]dx, 默认情况下 ρ ( x ) = 1 \rho(x)=1 ρ(x)=1, 故 A k = ∫ a b l k ( x ) d x A_k=\int_a^b l_k(x) dx Ak=∫ablk(x)dx
判断一个公式是否是插值型求积公式, 通过判断其求积系数是否满足 A k = ∫ a b l k ( x ) d x A_k = \int_a^b l_k(x) dx Ak=∫ablk(x)dx. 若满足则为插值型求积公式
由上面的代数精度定理, 可以知道 n + 1 n+1 n+1 个互不相同的节点 { x 0 , x 1 , . . . , x n } \{x_0,x_1,...,x_n\} {x0,x1,...,xn} 一定至少具有 n n n 次代数精度, 进一步插值型求积公式可以通过 A k = ∫ a b l k ( x ) d x A_k = \int_a^b l_k(x) dx Ak=∫ablk(x)dx 来确定求积系数
例题
对 ∫ 0 3 f ( x ) d x \int_0^3 f(x) dx ∫03f(x)dx 构造一个至少具有3次代数精度的求积公式
解析
-
至少 n = 3 n=3 n=3 次代数精度 ⇒ \Rightarrow ⇒ 使用具有 n + 1 = 4 n+1=4 n+1=4 个任意的插值节点的插值型求积公式必定能够满足要求, 取 { 0 , 1 , 2 , 3 } \{0,1,2,3\} {0,1,2,3}
-
相应的拉格朗日基函数
l 0 ( x ) = ( x − x 1 ) ( x − x 2 ) ( x − x 3 ) ( x 0 − x 1 ) ( x 0 − x 2 ) ( x 0 − x 3 ) = ( x − 1 ) ( x − 2 ) ( x − 3 ) ( 0 − 1 ) ( 0 − 2 ) ( 0 − 3 ) l 1 ( x ) = ( x − x 0 ) ( x − x 2 ) ( x − x 3 ) ( x 1 − x 0 ) ( x 1 − x 2 ) ( x 1 − x 3 ) = ( x − 0 ) ( x − 2 ) ( x − 3 ) ( 1 − 0 ) ( 1 − 2 ) ( 1 − 3 ) l 2 ( x ) = ( x − x 0 ) ( x − x 1 ) ( x − x 3 ) ( x 2 − x 0 ) ( x 2 − x 1 ) ( x 2 − x 3 ) = ( x − 0 ) ( x − 1 ) ( x − 3 ) ( 2 − 0 ) ( 2 − 1 ) ( 2 − 3 ) l 3 ( x ) = ( x − x 0 ) ( x − x 1 ) ( x − x 2 ) ( x 3 − x 0 ) ( x 3 − x 1 ) ( x 3 − x 2 ) = ( x − 0 ) ( x − 1 ) ( x − 2 ) ( 3 − 0 ) ( 3 − 1 ) ( 3 − 2 ) l_0(x)=\frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} = \frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)}\\l_1(x)=\frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} = \frac{(x-0)(x-2)(x-3)}{(1-0)(1-2)(1-3)}\\l_2(x)=\frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)} = \frac{(x-0)(x-1)(x-3)}{(2-0)(2-1)(2-3)}\\l_3(x)=\frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)} = \frac{(x-0)(x-1)(x-2)}{(3-0)(3-1)(3-2)} l0(x)=(x0−x1)(x0−x2)(x0−x3)(x−x1)(x−x2)(x−x3)=(0−1)(0−2)(0−3)(x−1)(x−2)(x−3)l1(x)=(x1−x0)(x1−x2)(x1−x3)(x−x0)(x−x2)(x−x3)=(1−0)(1−2)(1−3)(x−0)(x−2)(x−3)l2(x)=(x2−x0)(x2−x1)(x2−x3)(x−x0)(x−x1)(x−x3)=(2−0)(2−1)(2−3)(x−0)(x−1)(x−3)l3(x)=(x3−x0)(x3−x1)(x3−x2)(x−x0)(x−x1)(x−x2)=(3−0)(3−1)(3−2)(x−0)(x−1)(x−2)
-
计算求积系数 A k = ∫ 0 3 l k ( x ) d x A_k = \int_0^3 l_k(x) dx Ak=∫03lk(x)dx
-
插值型求积公式 ∫ 0 3 f ( x ) d x = A 0 × f ( 0 ) + A 1 × f ( 1 ) + A 2 × f ( 2 ) + A 3 × f ( 3 ) \int_0^3 f(x) dx=A_0 \times f(0) + A_1 \times f(1) + A_2 \times f(2) + A_3 \times f(3) ∫03f(x)dx=A0×f(0)+A1×f(1)+A2×f(2)+A3×f(3)
求积公式的稳定性
若求积系数 A k > 0 , k = 0 , 1 , 2 , . . . A_k > 0, k=0,1,2,... Ak>0,k=0,1,2,..., 则称求积公式是稳定的
插值型求积公式的余项(截断误差)
R [ f ] = ∫ a b f ( x ) d x − ∫ a b L n ( x ) d x = ∫ a b f ( x ) − ∑ k = 0 n ( l k ( x ) × y k ) d x = ∫ a b f ( n + 1 ) ( ϵ ) ( n + 1 ) ! ∏ i = 0 n ( x − x i ) d x = ∫ a b f ( n + 1 ) ( ϵ ) ( n + 1 ) ! w n + 1 ( x ) d x \begin{array}{ll} R[f] &=& \int_a^b f(x) dx - \int_a^b L_n(x) dx \\ \\ &=& \int_a^b f(x) - \sum_{k=0}^n (l_k(x) \times y_k) dx \\ \\ &=& \int_a^b \frac{f^{(n+1)}(\epsilon)}{(n+1)!}\prod_{i=0}^{n}(x-x_i)dx \\ \\ &=& \int_a^b \frac{f^{(n+1)}(\epsilon)}{(n+1)!} w_{n+1}(x)dx \\ \end{array} R[f]====∫abf(x)dx−∫abLn(x)dx∫abf(x)−∑k=0n(lk(x)×yk)dx∫ab(n+1)!f(n+1)(ϵ)∏i=0n(x−xi)dx∫ab(n+1)!f(n+1)(ϵ)wn+1(x)dx
Newton-Cotes(牛顿-柯斯特)公式
作为插值型求积公式中一类特殊且常用的形式, 额外限制了求积点的选择(等距节点), 即 h = b − a n , x k = a + k × h h = \frac{b-a}{n}, x_k = a + k \times h h=nb−a,xk=a+k×h, 默认包含了两个端点
∫ a b f ( x ) d x = ∑ k = 0 n ( f ( x k ) × A k ) = ( b − a ) × ∑ k = 0 n ( f ( x k ) × C k ( n ) ) \begin{array}{ll} \int_a^b f(x) dx &=& \sum_{k=0}^n (f(x_k) \times A_k ) \\ \\ &=& (b-a)\times \sum_{k=0}^n (f(x_k) \times C^{(n)}_k ) \end{array} ∫abf(x)dx==∑k=0n(f(xk)×Ak)(b−a)×∑k=0n(f(xk)×Ck(n))
其中: C k ( n ) C_k^{(n)} Ck(n) 称为Cotes系数, 满足 C k ( n ) = 1 b − a A k = ( − 1 ) n − k n × k ! × ( n − k ) ! ∫ 0 n ∏ i = 0 , i ≠ k n ( t − i ) d t C_k^{(n)} = \frac{1}{b-a} A_k = \frac{(-1)^{n-k}}{n \times k! \times (n-k)!} \int_0^n \prod_{i=0, i\ne k}^n(t-i)dt Ck(n)=b−a1Ak=n×k!×(n−k)!(−1)n−k∫0n∏i=0,i=kn(t−i)dt
| n\k | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | nan | |||
| 1 | 1/2 | 1/2 | ||
| 2 | 1/6 | 4/6 | 1/6 | |
| 3 | 1/8 | 3/8 | 3/8 | 1/8 |
Newton求积公式的代数精度
- 如果 n n n 是偶数, 代数精度为 n + 1 n+1 n+1
- 如果 n n n 是奇数, 代数精度为 n n n
Newton求积公式的截断误差
n = 1 梯形公式 : R [ f ] = − ( b − a ) 3 12 f ( 2 ) ( ϵ ) n = 2 辛普森公式 : R [ f ] = − ( b − a ) 5 2880 f ( 4 ) ( ϵ ) \begin{array}{ll} n=1 & 梯形公式 &:& R[f] &=& -\frac{(b-a)^3}{12}f^{(2)}(\epsilon) \\ \\ n=2 & 辛普森公式 &:& R[f] &=& -\frac{(b-a)^5}{2880}f^{(4)}(\epsilon) \\ \end{array} n=1n=2梯形公式辛普森公式::R[f]R[f]==−12(b−a)3f(2)(ϵ)−2880(b−a)5f(4)(ϵ)
n n n 阶Newton求积公式 ⇒ \Rightarrow ⇒ h ( n ) h(n) h(n) 次代数精度 ⇒ \Rightarrow ⇒ h ( n ) + 1 h(n) + 1 h(n)+1 阶导数 ⇒ \Rightarrow ⇒ ( b − a ) h ( n ) + 2 (b-a)^{h(n)+2} (b−a)h(n)+2
例题
分别使用梯形公式和辛普森公式计算积分 ∫ 1 2 e 1 x d x \int_1^2 e^{\frac{1}{x}} dx ∫12ex1dx 的近似值, 并估计截断误差
复化求积公式
使用区间越大, 根据插值公式的余项可以分析出需要更大的 n n n 才能保持相应的精度. 一方面, 当 n n n 越大时, C k ( n ) C_k^{(n)} Ck(n) 不方便计算; 另一方面, 当 n > 8 n>8 n>8 时, A k ≯ 0 A_k \not\gt 0 Ak>0, 因此求积公式也是不稳定的
因此, 将区间划分为小区间, 在每个小区间上分别使用低阶的Newton插值公式
Gauss型求积公式
给定 n + 1 n+1 n+1 个求积点, 可以得到 2 n + 1 2n+1 2n+1 次代数精度的求积公式, 不一定包含区间端点(大概率不包含)
一般的插值型求积公式: 任意求积点 ⇒ \Rightarrow ⇒ Newton求积公式: 等距求积点 ⇒ \Rightarrow ⇒ Gauss求积公式: 正交多项式的零点作为求积点
算法流程
- 计算满足 2 n + 1 2n+1 2n+1 次代数精度的求积公式 ⇒ \Rightarrow ⇒ n + 1 n+1 n+1 个求积点
- 选用或计算出正交多项式 g n + 1 ( x ) g_{n+1}(x) gn+1(x)
- 如果是满足常用的正交多项式的使用条件, 则直接使用公式结论, 例如Legendre多项式和Chebyshev多项式
- 如果不是常用的正交多项式, 则通过多项式正交化算法计算
- 得到正交多项式的零点, 即高斯求积点, 满足 g n + 1 ( x ) = 0 ⇒ x k = ? , k = 0 , 1 , . . . , n g_{n+1}(x)=0 \Rightarrow x_k=?, k=0,1,...,n gn+1(x)=0⇒xk=?,k=0,1,...,n
- 计算求积系数 A k = ∫ a b [ ρ ( x ) × l k ( x ) ] d x A_k = \int_a^b [\rho(x) \times l_k(x)] dx Ak=∫ab[ρ(x)×lk(x)]dx
- 确定高斯求积公式 G ( x ) = ∑ k = 0 n ( A k × f ( x k ) ) G(x) = \sum_{k=0}^n (A_k \times f(x_k)) G(x)=∑k=0n(Ak×f(xk))
常用的Gauss型求积公式(一): Gauss-Legendre求积公式
Legendre多项式的使用条件:
- 积分区间 [ − 1 , 1 ] [-1,1] [−1,1], 如果不满足需要进行换元
- 权函数 ρ ( x ) = 1 \rho(x)=1 ρ(x)=1

常用的Gauss型求积公式(二): Gauss-Chebyshev求积公式
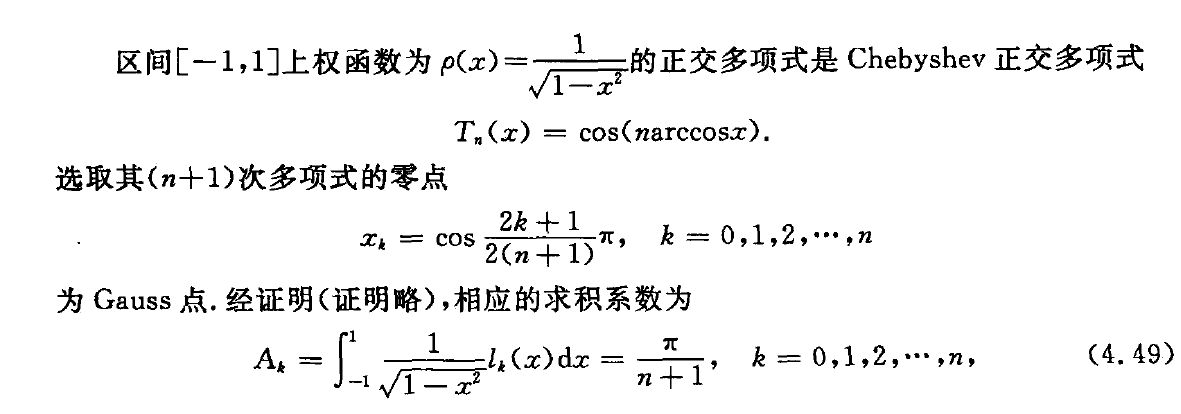
常微分方程的数值方法
预测-校正系统
-
预测: 用显式法计算下一步或下n步的值,
-
校正: 将预测值代入到隐式法中进行求解, 修正预测值
Euler方法
显式Euler公式
向前差分公式 $y’(x_k) &\approx& \frac{y(x_{k+1})-y(x_{k})}{x_{k+1}-x_{k}} \$ 得
y ( x k + 1 ) = y ( x k ) + Δ x × y ′ ( x k ) y k + 1 = y k + h × y k ′ \begin{array}{lll} y(x_{k+1}) &=& y(x_{k}) + \Delta x \times y'(x_{k}) \\ \\ y_{k+1} &=& y_{k} + h \times y'_{k} \\ \end{array} y(xk+1)yk+1==y(xk)+Δx×y′(xk)yk+h×yk′
def euler(x0, y0, threshold, h, f):"""显式Euler方法:param x0: x初值:param y0: y初值:param threshold: 上界,阈值:param h: 步长:param f: 导函数, 即y':return: 包含迭代过程中出现的(x,y)坐标的一个字典"""x = x0y = y0xList = [x]yList = [y]result = {'x': xList,'y': yList}while True:# 终止条件if x >= threshold:break# 迭代公式y = y + h * f(x, y)# 更新x, 推进迭代过程x = x + h# 保存数据result['x'].append(x)result['y'].append(y)return result
隐式Euler公式
由向后差分公式 y ′ ( x k + 1 ) ≈ y ( x k + 1 ) − y ( x k ) x k + 1 − x k y'(x_{k+1}) \approx \frac{y(x_{k+1})-y(x_{k})}{x_{k+1}-x_{k}} y′(xk+1)≈xk+1−xky(xk+1)−y(xk) 得
y k + 1 = y k + h × y k + 1 ′ y_{k+1} = y_{k} + h \times y'_{k+1} yk+1=yk+h×yk+1′
当 y ′ y' y′ 是 y y y 的线性函数, 即函数表达式的形式满足 y ′ = g ( x ) × y + t ( x ) y' = g(x) \times y + t(x) y′=g(x)×y+t(x) 时, 有
y k + 1 = y k + h × y k + 1 ′ = y k + h × [ g ( x k + 1 ) × y k + 1 + t ( x k + 1 ) ] = y k + h × t ( x k + 1 ) 1 − h × g ( x k + 1 ) \begin{array}{ll} y_{k+1} &=& y_{k} + h \times y'_{k+1} \\ \\ &=& y_k + h \times [g(x_{k+1}) \times y_{k+1} + t(x_{k+1})] \\ \\ &=& \frac{y_k + h \times t(x_{k+1})}{1-h \times g(x_{k+1})} \\ \end{array} yk+1===yk+h×yk+1′yk+h×[g(xk+1)×yk+1+t(xk+1)]1−h×g(xk+1)yk+h×t(xk+1)
def implicitEuler(x0, y0, threshold, h, g, t):"""隐式Euler方法:param x0: x初值:param y0: y初值:param threshold: 上界,阈值:param h: 步长:param g: y'=g*y+t:param t: y'=g*y+t:return: 包含迭代过程中出现的(x,y)坐标的一个字典"""x = x0y = y0xList = [x]yList = [y]result = {'x': xList,'y': yList}while True:# 终止条件if x >= threshold:break# 迭代公式, 注意这里是 t(x+h)y = (y + h * t(x + h)) / (1 - h * g(x))# 更新x, 推进迭代过程x = x + h# 保存数据result['x'].append(x)result['y'].append(y)return result
梯形公式
加权平均 ⇒ \Rightarrow ⇒ Runge-Kutta方法
y k + 1 = y k + h × ( 1 2 y k ′ + 1 2 y k + 1 ′ ) \begin{array}{ll} y_{k+1} &=& y_{k} + h \times (\frac{1}{2}y'_{k} + \frac{1}{2}y'_{k+1}) \\ \end{array} yk+1=yk+h×(21yk′+21yk+1′)
同样在满足 y ′ = g ( x ) × y + t ( x ) y' = g(x) \times y + t(x) y′=g(x)×y+t(x) 条件后, 有
y k + 1 = y k + h × ( 1 2 y k ′ + 1 2 y k + 1 ′ ) = y k + h × 1 2 ( g ( x k ) × y ( x k ) + t ( x k ) + g ( x k + 1 ) × y ( x k + 1 ) + t ( x k + 1 ) ) = ( 1 + 1 2 × h × g ( x k ) ) × y ( x k ) + 1 2 × h × ( t ( x k ) + t ( x k + 1 ) ) 1 − 1 2 × h × g ( x k + 1 ) = ( 2 + h × g k ) × y k + h × ( t k + t k + 1 ) 2 − h × g k + 1 \begin{array}{ll} y_{k+1} &=& y_{k} + h \times (\frac{1}{2}y'_{k} + \frac{1}{2}y'_{k+1}) \\ \\ &=& y_{k} + h \times \frac{1}{2}(g(x_{k})\times y(x_k) + t(x_k) + g(x_{k+1}) \times y(x_{k+1}) + t(x_{k+1})) \\ \\ &=& \frac{(1+\frac{1}{2} \times h \times g(x_k))\times y(x_k) + \frac{1}{2} \times h \times (t(x_{k}) + t(x_{k+1}))}{1-\frac{1}{2}\times h \times g(x_{k+1})} \\ \\ &=& \frac{(2+ h \times g_k)\times y_k + h\times (t_{k} + t_{k+1})}{2- h \times g_{k+1}} \\ \end{array} yk+1====yk+h×(21yk′+21yk+1′)yk+h×21(g(xk)×y(xk)+t(xk)+g(xk+1)×y(xk+1)+t(xk+1))1−21×h×g(xk+1)(1+21×h×g(xk))×y(xk)+21×h×(t(xk)+t(xk+1))2−h×gk+1(2+h×gk)×yk+h×(tk+tk+1)
def middleEuler(x0, y0, threshold, h, g, t):"""梯形公式Euler方法:param x0: x初值:param y0: y初值:param threshold: 上界,阈值:param h: 步长:param g: y'=g*y+t:param t: y'=g*y+t:return: 包含迭代过程中出现的(x,y)坐标的一个字典"""x = x0y = y0xList = [x]yList = [y]result = {'x': xList,'y': yList}while True:# 终止条件if x >= threshold:break# 迭代公式y = ((2 + h * g(x)) * y + h * (t(x) + t(x + h))) / (2 - h * g(x + h))# 更新x, 推进迭代过程x = x + h# 保存数据result['x'].append(x)result['y'].append(y)return result改进Euler公式
不需要隐式法中额外的限制条件, 能够应用于更多的场合
- 显式Euler公式预测
- 梯形公式校正
y k + 1 ( 1 ) = y k + h × f ( x k , y k ) y k + 1 = y k + h × f ( x k , y k ) + f ( x k + 1 , y k + 1 ( 1 ) ) 2 \begin{array}{ll} y_{ k + 1 }^{(1)} &=& y _ { k } + h \times f ( x _ { k } , y _ { k } ) \\ \\ y_{k + 1} &=& y _ { k } + h \times \frac { f ( x _ { k } , y _ { k } ) + f ( x _ { k + 1 } , y^{(1)}_{ k + 1 } ) } { 2 } \\ \end{array} yk+1(1)yk+1==yk+h×f(xk,yk)yk+h×2f(xk,yk)+f(xk+1,yk+1(1))
def optimizateEuler(x0, y0, threshod, h, f):x = x0y = y0xList = [x]yList = [y]result = {'x': xList,'y': yList}while True:if x >= threshod:break# euler公式预测y_tmp = y + h * f(x, y)# 改进euler公式校正y = y + h * (f(x, y) + f(x + h, y_tmp)) / 2x = x + h# 保存数据result['x'].append(x)result['y'].append(y)return result
局部截断误差
对于任意一个常微分方程问题, 假设能够解出其精确解 y ( x ) y(x) y(x), 那么在同一基准线上, 仅仅比较下一次精确解的准确值和迭代公式的估计值的差即为局部截断误差.
T n + 1 = y ( x n + h ) − y ^ n + 1 ( x n , y n ) = y ( x n + h ) − [ y ( x n ) + h × y ′ ( x n ) ] = y ( x n ) + y ′ ( x n ) × h + y ′ ′ ( x n ) 2 ! × h 2 + O ( h 3 ) − [ y ( x n ) + h × y ′ ( x n ) ] ( 泰勒展开 ) = y ′ ′ ( x n ) 2 ! × h 2 + O ( h 3 ) \begin{array}{ll} T_{n+1} &=& y(x_{n} + h) - \hat{y}_{n+1}(x_n, y_n)\\ \\ &=& y(x_{n}+h) - [y(x_n) + h \times y'(x_n)]\\ \\ &=& y(x_n) + y'(x_n) \times h + \frac{y''(x_n)}{2!} \times h^2 + O(h^3) - [y(x_n) + h \times y'(x_n)] &(泰勒展开)\\ \\ &=& \frac{y''(x_n)}{2!} \times h^2 + O(h^3) \end{array} Tn+1====y(xn+h)−y^n+1(xn,yn)y(xn+h)−[y(xn)+h×y′(xn)]y(xn)+y′(xn)×h+2!y′′(xn)×h2+O(h3)−[y(xn)+h×y′(xn)]2!y′′(xn)×h2+O(h3)(泰勒展开)
之所以称之为局部截断误差, 是因为除了在初值条件的时候, 精确解和迭代公式都不在同一基准线上, 迭代公式每一步都会产生误差, 因此逐渐偏离基准线, 整体截断误差应该表示为 y ( x n + h ) − y ^ n + 1 ( x n , y ^ n ) y(x_n+h)-\hat{y}_{n+1}(x_n, \hat{y}_n) y(xn+h)−y^n+1(xn,y^n)
Runge-Kutta方法(略)
加权平均 ⇒ \Rightarrow ⇒ Runge-Kutta方法
y k + 1 = y k + h × ( ∑ i = 0 n ( λ i × k i ) \begin{array}{ll} y_{k+1} &=& y_{k} + h \times (\sum_{i=0}^{n}(\lambda_i \times k_i) \\ \end{array} yk+1=yk+h×(∑i=0n(λi×ki)
其中: k i k_i ki 满足一系列规则
收敛性与稳定性
单步法的收敛性
没懂
单步法的(绝对)稳定性
绝对稳定性用来对步长的选取进行限制, 不能任意选择
通过Taylor展开并局部线性化, 一般形式的一阶微分方程总可以化作如下的模型方程
y ′ = ∂ y ′ ( x , y ) ∂ y × y = ∂ f ( x , y ) ∂ y × y = λ × y \begin{array}{ll} y' &=& \frac{\partial y'(x,y)}{\partial y} \times y \\ \\ &=& \frac{\partial f(x,y)}{\partial y} \times y \\ \\ &=& \lambda \times y \\ \end{array} y′===∂y∂y′(x,y)×y∂y∂f(x,y)×yλ×y
单步法经过整理后, 可以得到形式如下
y n + 1 = E ( λ h ) × y n 其中 E ( λ h ) 由选择的方法决定 \begin{array}{ll} y_{n+1} &=& E(\lambda h) \times y_n &其中E(\lambda h)由选择的方法决定\\ \end{array} yn+1=E(λh)×yn其中E(λh)由选择的方法决定
误差传播公式同上
e n + 1 = E ( λ h ) × e n \begin{array}{ll} e_{n+1} &=& E(\lambda h) \times e_n \\ \end{array} en+1=E(λh)×en
为保证绝对稳定, 因此需要满足条件 ∣ E ( λ h ) ∣ ≤ 1 |E(\lambda h)| \le 1 ∣E(λh)∣≤1
线性方程组的解法
非线性方程的解法
特征值和特征向量的计算
幂法与反幂法
- 幂法: 适用于计算矩阵的主特征值(模最大的特征值)和对应的特征向量
- 反幂法: 用于计算矩阵的模最小特征值及其特征向量, 还可以用来计算给定近似特征值的特征向量
幂法算法流程
-
任取一个非零向量 u 0 = k 1 e 1 + k 2 e 2 + ⋯ k n e n u_0 = k_1 e_1 + k_2 e_2 + \cdots k_n e_n u0=k1e1+k2e2+⋯knen
-
迭代公式
u k = A ⋅ u k − 1 = A k ⋅ u 0 = A k ⋅ ( k 1 e 1 + k 2 e 2 + ⋯ k n e n ) ≈ ( λ 1 k k 1 ) e 1 ( k 足够大时 ) \begin{array}{ll} u_{k} &=& A \cdot u_{k-1} \\ \\ &=& A^k \cdot u_0 \\ \\ &=& A^k \cdot (k_1 e_1 + k_2 e_2 + \cdots k_n e_n) \\ \\ &\approx& (\lambda_1^k k_1) e_1 &(k足够大时) \end{array} uk===≈A⋅uk−1Ak⋅u0Ak⋅(k1e1+k2e2+⋯knen)(λ1kk1)e1(k足够大时) -
因为 e 1 e_1 e1 是特征向量, u k u_k uk 作为 e 1 e_1 e1 的近似, 因此 u k u_k uk 作为矩阵 A A A 的主特征向量的近似 (向量之间, 方向是最基本的, 系数都是次要的)
-
使用归一化 u k = u k ∣ ∣ u k ∣ ∣ u_k = \frac{u_k}{||u_k||} uk=∣∣uk∣∣uk 控制系数, 防止系数对误差的影响
)




)
)

)

)








