快速排序算法最早是由图灵奖获得者Tony Hoare设计出来的,他在形式化方法理论以 及ALGOL.60编程语言的发明中都有卓越的贡献,是20世纪最伟大的计算机科学家之—。 而这快速排序算法只是他众多贡献中的—个小发明而已。
快速排序(Quick Sort)的基本算法思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可以分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
接下来我们一起来认识一下快排。
霍尔版本
快排共有三种实现方法,最初的一代就是创始人霍尔的版本;

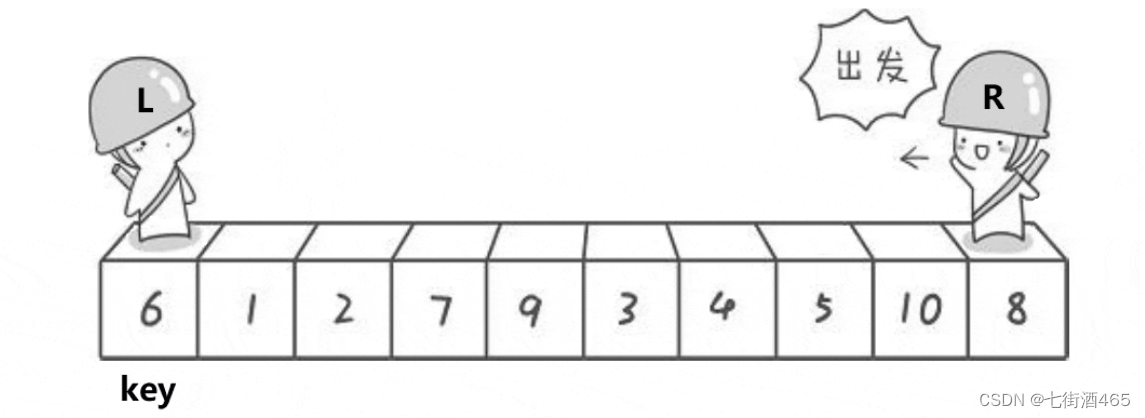
霍尔版本是数组的数,选定数组第一个位置keyi,然后从数组的最右边right=n-1往前一个个找到比keyi位置小的数,接下来从最左边left=0开始,找到第一个比Keyi位置大的数,然后交换刚才找到的右边小的数和左边大的数;接下来继续从右边找小,从左边找大,等到right和left相遇时,停下,此时再交换keyi和left(right)位置的数,那么,比这个key小的数都在key的左边,比Key大的数都在key的右边,再递归0到keyi-1,keyi+1到n-1位置的数,如此下来就可以得到有序的数据。
接下来我们开始实现
int PartSort1(int* a, int left, int right)
{int keyi = left;while (left < right)//left和right相遇时循环停下{while (left<right&&a[right] >= a[keyi])//找小{right--;//right没找到小right--往下走}while (left < right && a[left] <= a[keyi])//找大{left++;//left没找到大left++往下走}Swap(&a[left], &a[right]);//将找到的小的和大的交换位置}Swap(&a[left], &a[keyi]);//最后left和keyi交换位置return left;
}这是一趟keyi的找大找小过程,一个过程只能确定一个数的位置,我们还需要继续递归keyi的左边和keyi的右边。
int keyi = PartSort1(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi+1, end);
但是什么时候停止呢?当区间只有一个数的时候就需要停止,即begin==end时候return。但是还可能存在只剩区间【0,0】时,此时keyi=1,begin=0,keyi-1=0;keyi+1=2,end=0,发生不存在区间,所以就会停止。

void QuickSort(int* a, int begin,int end)
{if (begin >= end)//{return;}int keyi = PartSort1(a, begin, end);//每次可以确定一个keyi位置,保证不再变动QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}上述partsort1版本就是霍尔版本的快排。
挖坑法
第二个实现快排的方法是挖坑法
挖坑法呢其实就是也是从a[0]开始,记key=a[0],在最开始处即a[0]处定义一个hole(坑),从右边开始找比key小的值,找到了把a[right]处赋给上一个hole,使right现在的位置为新的hole,再从左边left处找到比key大的值,把a[left]的值赋给上一个hole,使left现在的位置为新的hole,下面我们一起实现。
int PartSort2(int* a, int left, int right)
{int key = a[left];int hole = left;while (left < right){while (left<right && a[right]>key){right--;}a[hole] = a[right];hole = right;while (left<right && a[left]<key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;//相遇后把最后一个hole位置的值给key;return hole;
}最后返回hole的位置,接下来就和上面一样,QuickSort直接调用PastSort2,然后递归就可以啦。
前后指针法
第三种实现快排的方法是 前后指针法,虽然说是前后指针,其实并不是使用指针,而是两个下标一前一后走。所谓前后指针法就是定义两个下标cur和pre,pre初始为Left,cur是left+1的位置,记录keyi=left的位置的值,cur从当前位置依次往后找比a[keyi]小的值,如果比a[keyi]大或者等于,cur就++往后走,如果小于a[lkeyi]的值,则pre要++,然后交换cur和pre的位置,直到cur走到末尾。最后在交换pre和keyi位置的数值,返回keyi位置就可以了。
下面我们实现
int PartSort3(int* a, int left, int right)
{int pre = left;int cur = left + 1;int keyi = left;while (cur <=right){if (a[cur] >= a[keyi])//找小{cur++;//没找到就++继续往下走}else{pre++;Swap(&a[pre], &a[cur]);//找到了就和++pre位置交换cur++;}}Swap(&a[keyi], &a[pre]);keyi = pre;return keyi;
}上述写法还可以优化,我们想,如果前几个cur位置都比a[keyi]小的话,也就是先++pre,再交换pre和cur位置,再++cur,可是本来最初cur就比pre提前一个位置,如果一组数据前几个数都是a[cur]<a[keyi]的话就一直是相同的cur位置和pre位置交换。我们可以写成
while (cur<=right)
{if (a[cur] < a[keyi] && ++pre != cur)//只有在pre++!=cur的情况下再交换{Swap(&a[cur], &a[pre]);}cur++;
}这样就可以减少不必要无意义的交换了。
以上就是三种快排的实现方法,个人而言觉得第三种前后指针法更简便,更容易实现。当然这三种方法并没有本质区别和性能区别,掌握哪种都一样,都能掌握当然是最好的。
#include<stdio.h>
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int PartSort1(int* a, int left, int right)//霍尔
{int keyi = left;while (left < right){while (left<right&&a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}
int PartSort2(int* a, int left, int right)//挖坑
{int key = a[left];int hole = left;while (left < right){while (left<right && a[right]>key){right--;}a[hole] = a[right];hole = right;while (left<right && a[left]<key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
int PartSort3(int* a, int left, int right)//前后指针
{int pre = left;int cur = left + 1;int keyi = left;/*while (cur <=right){if (a[cur] >= a[keyi]){cur++;}else{pre++;Swap(&a[pre], &a[cur]);cur++;}}*/while (cur <= right){if (a[cur] < a[keyi] && ++pre != cur){Swap(&a[cur], &a[pre]);}cur++;}Swap(&a[keyi], &a[pre]);keyi = pre;return keyi;
}
void QuickSort(int* a, int begin,int end)
{if (begin >= end){return;}int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
int main()
{int a[] = { 5,7,4,3,10,8,2,6,9,1 };QuickSort(a, 0,(sizeof(a) / sizeof(int))-1);return 0;
}




linux I2C驱动)

,底层数据结构是数组,编写add添加方法,正序打印和倒叙打印)





笔记】操作系统概论)

)


 概述)
