【MATLAB第83期】基于MATLAB的LSTM代理模型的SOBOL全局敏感性运用
引言
在前面几期,介绍了敏感性分析法,本期来介绍lstm作为代理模型的sobol全局敏感性分析模型。
【MATLAB第31期】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理回归问题MATLAB代码实现(持续更新)
【MATLAB第32期】【更新中】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理分类问题MATLAB代码实现
【MATLAB第63期】基于MATLAB的改进敏感性分析方法IPCC,拥挤距离与皮尔逊系数法结合实现回归与分类预测
【MATLAB第64期】【保姆级教程】基于MATLAB的SOBOL全局敏感性分析模型运用(含无目标函数,考虑代理模型)
二、SOBOL(无目标函数)
1.解决思路
(1)针对简单线性数据及非线性数据,用函数拟合得到公式,随后思路与上面一致。
(2)无法拟合得到公式, 即复杂非线性函数,需要通过借用机器学习模型,作为训练学习模型(黑箱子模型)
本文具体研究攻克第二种情况
有个前提(模型拟合性较好,对应数据较好)
即训练学习模型, 训练集和测试集拟合效果很棒。
如果拟合效果差,SOBOL分析结果一定存在较大误差。
2.模型选择
1、选用libsvm模型作为代理模型
原因:
(1)代理模型讲究运行效率快、精度高、模型简单 。libsvm符合以上情况,仅有的两超参数c、g经验值结果普遍较好,基本不用调参 。
(2)进行对比以bp为代表的神经网络模型,因其机理中涉及随机初始的权值阈值等参数,会让模型不够稳定。
(3)进行对比的rf随机森林模型, 训练效果远差于bp /libsvm ,且参数调整较为复杂。
(4)深度学习模型更适合大数据模型,对于平时用的小数据,传统模型不见得效果比深度模型差 ,其次深度学习运行时间、模型复杂程度,调参难度等问题明显无法与传统方法相比 。
2、选用lstm模型作为代理模型**
(1)训练精度较高,sobol误差更小,结果更令人信服。
(2)收敛速度较慢。
3.数据设置:常用的案例数据 ,103*8 ,前7列代表输入变量, 最后1列代表因变量。
4.选用模型后,几个点需要注意:
(1)数据固定,即训练样本/测试样本固定, 所代表的模型评价才够稳定。
(2)使用固定算子函数代码(神经网络代理模型是必要的) ,即开头代码为: rng default 或者rng(M)等 ,M根据实际测试效果确定。可固定输出结果,保证运行结果一致。此一致代表此刻你打开的matlab, 在不关闭情况下每次运行结果一致。跟matlab版本有关,系统版本,以及电脑有关。
(3)最为关键的一点 ,变量的上下限不能超过案例数据的上下限,为了保证模型的普适性和有效性!!!
比如案例数据的训练样本中, X1-X7的最小值为:
[137 0 0 160 4.4 708 650]
X1-X7的最大值为:
[374 193 260 240 19 1049.90 902]
那么你的sobol序列生成的数据也只能在这个范围,才能保证代理模型的有效性。
(4)生成样本的数量当然以多为好, 但不能跟案例数据样本数量差距太大,减少偶然性。
(5)代理模型效果(以lstm为例)
训练集数据的R2为:0.98842
测试集数据的R2为:0.97992
训练集数据的MAE为:0.653
测试集数据的MAE为:0.79625
训练集数据的MBE为:0.12945
测试集数据的MBE为:0.32146

个人认为,训练集和测试集R2如果均大于0.95还是可以的,评价指标好坏全凭主观意思。包括评价指标的选择,不一定是R2,R2更适合这样的波动的曲线 。
(6)保存模型所需要的变量
save lstmnet model ps_output ps_input
通过sobol生成样本进行仿真预测。
3.SOBOL模型分析
(1)sobol参数设置
%% 设定:给定参数个数和各个参数的范围
D=7;% 7个参数
M=D*2;%
nPop=80;% 采样点个数,跟训练样本数量大概一致
VarMin=[137 0 0 160 4.4 708 650];%各个参数下限
VarMax=[374 193 260 240 19 1049.90 902];%各个参数上限
nPop=200
(2)运行结果
敏感程度(libsvm作为代理模型):X4>X3≈X1>X7>X6>X5>X2
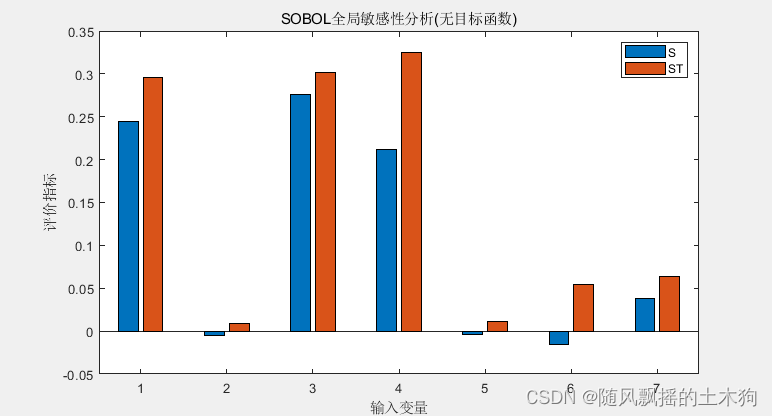
敏感程度(lstm作为代理模型):X2>X1>X3>X7>X6>X2>X5
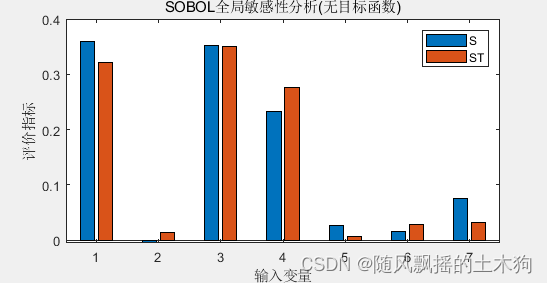
lstm总体来说与svm敏感性结果差异不大。
三、代码获取
其中,lstm代理模型的目标函数加密,不影响使用。
私信回复“83期”即可获取下载链接。
)

)
)













)

