SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测
目录
- SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测
- 预测效果
- 基本介绍
- 程序设计
- 参考资料
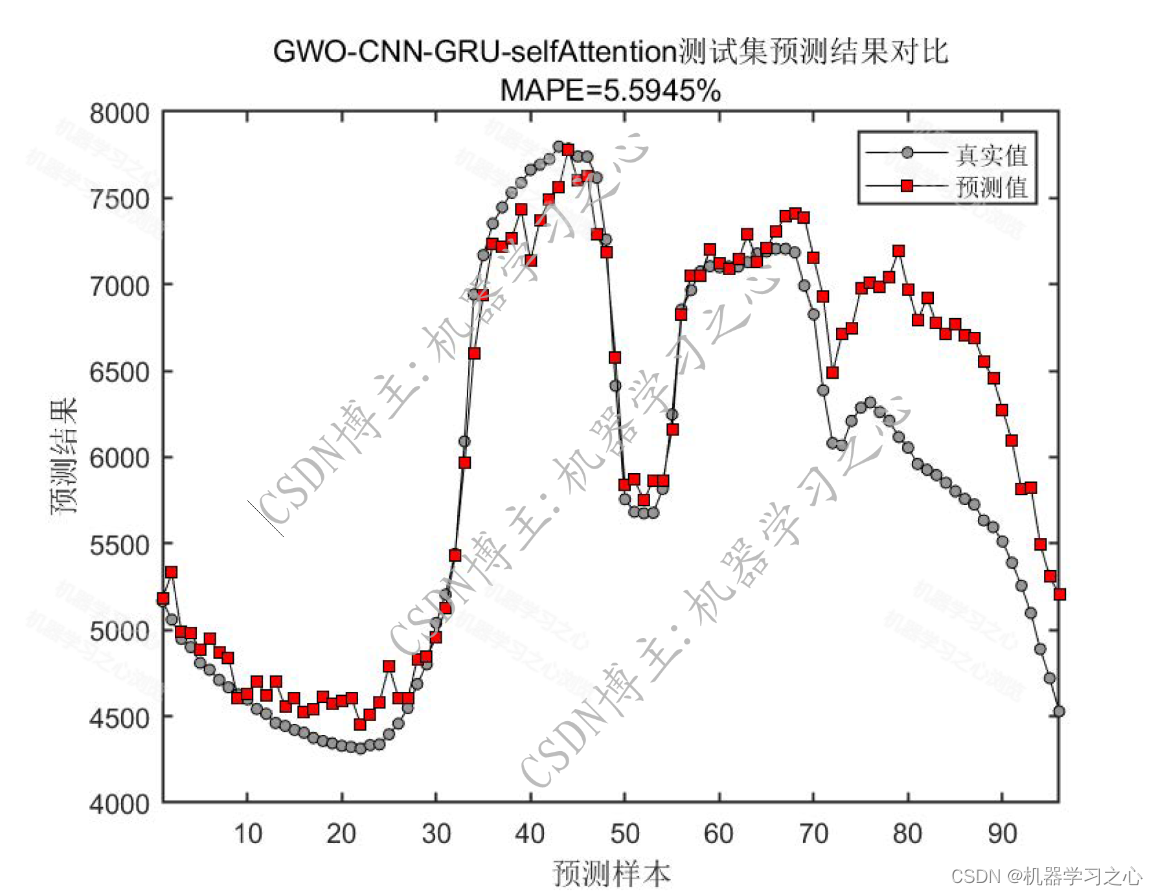
预测效果






基本介绍
1.Matlab实现GWO-CNN-GRU-selfAttention灰狼算法优化卷积门控循环单元融合自注意力机制多变量多步时间序列预测,灰狼算法优化学习率,卷积核大小,神经元个数,以最小MAPE为目标函数;

CNN卷积核大小:卷积核大小决定了CNN网络的感受野,即每个卷积层可以捕获的特征的空间范围。选择不同大小的卷积核可以影响模型的特征提取能力。较小的卷积核可以捕获更细粒度的特征,而较大的卷积核可以捕获更宏观的特征。
GRU门控单元个数:GRU是一种适用于序列数据的循环神经网络,其神经元个数决定了模型的复杂性和记忆能力。较多的GRU神经元可以提高模型的学习能力,但可能导致过拟合。
学习率:学习率是训练深度学习模型时的一个关键超参数,它控制每次参数更新的步长。学习率过大可能导致模型不稳定和发散,学习率过小可能导致训练过慢或陷入局部最小值。
自注意力层 (Self-Attention):Self-Attention自注意力机制是一种用于模型关注输入序列中不同位置相关性的机制。它通过计算每个位置与其他位置之间的注意力权重,进而对输入序列进行加权求和。自注意力能够帮助模型在处理序列数据时,对不同位置的信息进行适当的加权,从而更好地捕捉序列中的关键信息。在时序预测任务中,自注意力机制可以用于对序列中不同时间步之间的相关性进行建模。
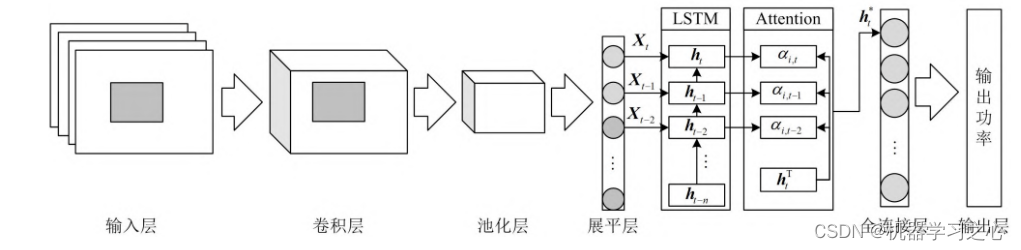
2.运行环境为Matlab2023a及以上,提供损失、RMSE迭代变化极坐标图;网络的特征可视化图;测试对比图;适应度曲线(若首轮精度最高,则适应度曲线为水平直线);
3.excel数据集(负荷数据集),输入多个特征,输出单个变量,考虑历史特征的影响,多变量多步时间序列预测(多步预测即预测下一天96个时间点),main.m为主程序,运行即可,所有文件放在一个文件夹;
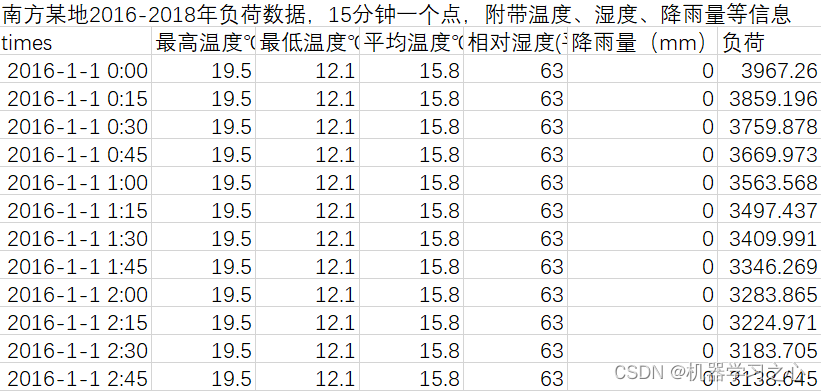
4.命令窗口输出SSE、RMSE、MSE、MAE、MAPE、R2、r多指标评价;
适用领域:负荷预测、风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。
程序设计
- 完整程序和数据获取方式:私信博主回复Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测获取。
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% Grey Wolf Optimizer
% 灰狼优化算法function [Alpha_score, Alpha_pos, Convergence_curve, bestPred,bestNet,bestInfo ] = GWO(SearchAgents_no, Max_iter, lb, ub, dim, fobj)
% 输入参数:
% SearchAgents_no:搜索个体的数量
% Max_iter:最大迭代次数
% lb:搜索空间的下界(一个1维向量)
% ub:搜索空间的上界(一个1维向量)
% dim:问题的维度
% fobj:要优化的目标函数,输入为一个位置向量,输出为一个标量% 初始化alpha、beta和delta的位置向量
Alpha_pos = zeros(1, dim);
Alpha_score = inf; % 对于最小化问题,请将其改为-infBeta_pos = zeros(1, dim);
Beta_score = inf; % 对于最小化问题,请将其改为-infDelta_pos = zeros(1, dim);
Delta_score = inf; % 对于最小化问题,请将其改为-inf% 初始化领导者的位置向量和得分Positions = ceil(rand(SearchAgents_no, dim) .* (ub - lb) + lb);Convergence_curve = zeros(1, Max_iter);l = 0; % 迭代计数器% 主循环
while l < Max_iterfor i = 1:size(Positions, 1)% 将超出搜索空间边界的搜索代理放回搜索空间内Flag4ub = Positions(i, :) > ub;Flag4lb = Positions(i, :) < lb;Positions(i, :) = (Positions(i, :) .* (~(Flag4ub + Flag4lb))) + ub .* Flag4ub + lb .* Flag4lb;% 计算每个搜索个体的目标函数值[fitness,Value,Net,Info] = fobj(Positions(i, :));% 更新Alpha、Beta和Delta的位置向量if fitness < Alpha_scoreAlpha_score = fitness; % 更新Alpha的得分Alpha_pos = Positions(i, :); % 更新Alpha的位置向量bestPred = Value;bestNet = Net;bestInfo = Info;endif fitness > Alpha_score && fitness < Beta_scoreBeta_score = fitness; % 更新Beta的得分Beta_pos = Positions(i, :); % 更新Beta的位置向量endif fitness > Alpha_score && fitness > Beta_score && fitness < Delta_scoreDelta_score = fitness; % 更新Delta的得分Delta_pos = Positions(i, :); % 更新Delta的位置向量endenda = 2 - l * ((2) / Max_iter); % a从2线性减少到0% 更新搜索个体的位置向量for i = 1:size(Positions, 1)for j = 1:size(Positions, 2)r1 = rand(); % r1是[0,1]区间的随机数r2 = rand(); % r2是[0,1]区间的随机数A1 = 2 * a * r1 - a; % 参考文献中的公式(3.3)C1 = 2 * r2; % 参考文献中的公式(3.4)D_alpha = abs(C1 * Alpha_pos(j) - Positions(i, j)); % 参考文献中的公式(3.5)-part 1X1 = Alpha_pos(j) - A1 * D_alpha; % 参考文献中的公式(3.6)-part 1r1 = rand();r2 = rand();参考资料
[1] http://t.csdn.cn/pCWSp
[2] https://download.csdn.net/download/kjm13182345320/87568090?spm=1001.2014.3001.5501
[3] https://blog.csdn.net/kjm13182345320/article/details/129433463?spm=1001.2014.3001.5501


——异常值处理)








)







