一、主要目的:
主要利用Python包,如Numpy、Pandas和Scipy等常用分析工具并结合常用的统计量来进行数据的描述,把数据的特征和内在结构展现出来。熟悉在Python开发环境中支持数据分析的可用模块以及其中的方法,基于一定的样例数据,编写数据分析过程的示例代码。
二、主要内容:
1.基本统计分析
基本统计分析又叫描述性统计分析,一般统计某个变量的最小值、第一个四分位值、中值、第三个四分位值以及最大值。
数据的中心位置是我们最容易想到的数据特征。借由中心位置,我们可以知道数据的一个平均情况,如果要对新数据进行预测,那么平均情况是非常直观的选择。数据的中心位置可分为均值(Mean)、中位数(Median)和众数(Mode)。其中均值和中位数用于定量的数据,众数用于定性的数据。对于定量数据来说,均值是总和除以总量N,中位数是数值大小位于中间(奇偶总量处理不同)的值,均值相对中位数来说,包含的信息量更大,但是容易受异常的影响。
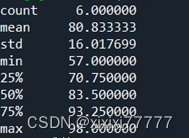
描述性统计分析函数为describe。该函数返回值有均值、标准差、最大值、最小值、分位数等。括号中可以带一些参数,如percentitles=[0.2,0.4,0.6,0.8]就是指定只计算0.2、0.4、0.6、0.8分位数,而不是默认的1/4、1/2、3/4 分位数。
常用的统计函数有:
size:计数(此函数不需要括号)
sum():求和
mean():平均值
var():方差
std():标准差
2.分组分析
分组分析是指根据分组字段将分析对象划分成不同的部分,以对比分析各组之间差异性的一种分析方法。
常用的统计指标有:计数、求和、平均值
3.分布分析
分布分析是指根据分析的目的,将数据(定量数据)进行等距或不等距的分组,研究各组分布规律的一种分析方法。
4.交叉分析
交叉分析通常用于分析两个或两个以上分组变量之间的关系,以交叉表形式进行变量间关系的对比分析。一般分为定量、定量分组交叉;定量、定性分组交叉;定性、定型分组交叉。常用命令格式如下:
pivot_table(values,index,columns,aggfunc,fill_value)
5.结构分析
结构分析是在分组分析以及交叉分析的基础上,计算各组成部分所占的比重,进而分析总体的内部特征的一种分析方法。
这里分组主要是指定性分组,定性分组一般看结构,它的重点在于计算各组成部分占总体的比重。
6.相关分析
判断两个变量是否具有线性相关关系最直观的方法是直接绘制散点图,看变量之间是否符合某个变化规律。当需要同时考察多个变量间的相关关系时,一一绘制他们间的简单散点图是比较麻烦的。此时可以利用散点矩阵图同时绘制各变量间的散点图,从而快速发现多个变量间的主要相关性,这在进行多元线性回归时显得尤为重要。
相关分析是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的相关关系的一种统计方法。
为了更加准确地描述变量之间的线性相关程度,通过计算相关系数来进行相关分析,在二元变量的相关分析过程中,比较常用的有Pearson相关系数、Spearman秩相关系数和判定系数。Pearson相关系数一般用于分析两个连续变量之间的关系,要求连续变量的取值服从正态分布。不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数(也称等级相关系数)来描述。
相关系数可以用来描述定量变量之间的关系。
三、实现过程:

四、源码附件:
import pandas as pd
import numpy as np
from pandas import Series, DataFrame
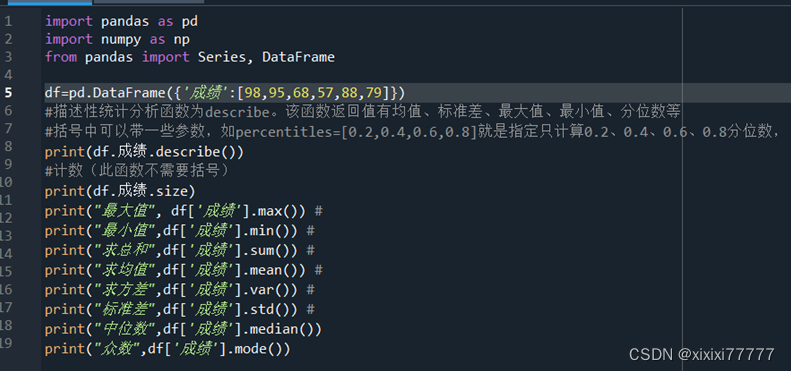
df=pd.DataFrame({'成绩':[98,95,68,57,88,79]})
#描述性统计分析函数为describe。该函数返回值有均值、标准差、最大值、最小值、分位数等
#括号中可以带一些参数,如percentitles=[0.2,0.4,0.6,0.8]就是指定只计算0.2、0.4、0.6、0.8分位数,
print(df.成绩.describe())
#计数(此函数不需要括号)
print(df.成绩.size)
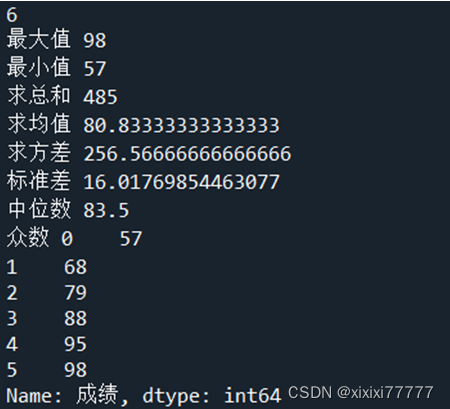
print("最大值", df['成绩'].max()) #
print("最小值",df['成绩'].min()) #
print("求总和",df['成绩'].sum()) #
print("求均值",df['成绩'].mean()) #
print("求方差",df['成绩'].var()) #
print("标准差",df['成绩'].std()) #
print("中位数",df['成绩'].median())
print("众数",df['成绩'].mode())
import pandas as pd
import numpy as np
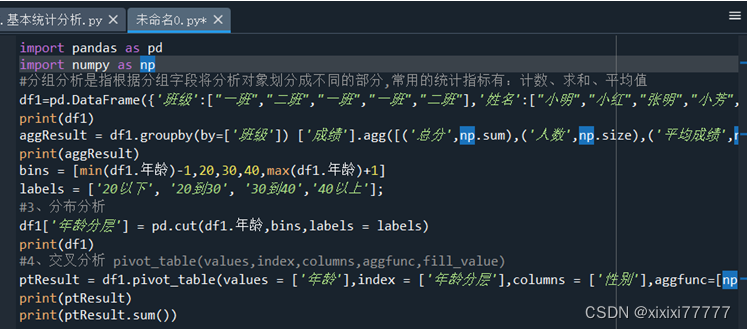
#分组分析是指根据分组字段将分析对象划分成不同的部分,常用的统计指标有:计数、求和、平均值
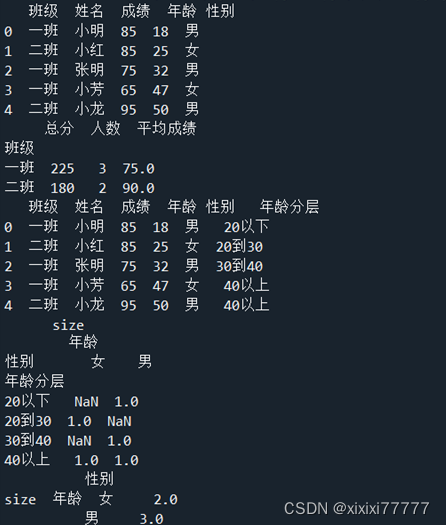
df1=pd.DataFrame({'班级':["一班","二班","一班","一班","二班"],'姓名':["小明","小红","张明","小芳","小龙"],'成绩':[85,85,75,65,95],'年龄':[18,25,32,47,50],'性别':['男','女','男','女','男']})
print(df1)
aggResult = df1.groupby(by=['班级']) ['成绩'].agg([('总分',np.sum),('人数',np.size),('平均成绩',np.mean)])
print(aggResult)
bins = [min(df1.年龄)-1,20,30,40,max(df1.年龄)+1]
labels = ['20以下', '20到30', '30到40','40以上'];
#3、分布分析
df1['年龄分层'] = pd.cut(df1.年龄,bins,labels = labels)
print(df1)
#4、交叉分析 pivot_table(values,index,columns,aggfunc,fill_value)
ptResult = df1.pivot_table(values = ['年龄'],index = ['年龄分层'],columns = ['性别'],aggfunc=[np.size])
print(ptResult)
print(ptResult.sum())
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 随机数生成器的种子
np.random.seed(19680801)
N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = (30 * np.random.rand(N))**2 # 0 to 15 point radii
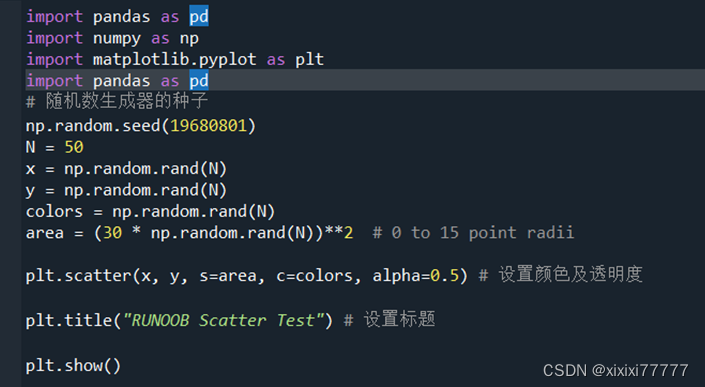
plt.scatter(x, y, s=area, c=colors, alpha=0.5) # 设置颜色及透明度
plt.title("RUNOOB Scatter Test") # 设置标题
plt.show()
import numpy as np
import pandas as pd
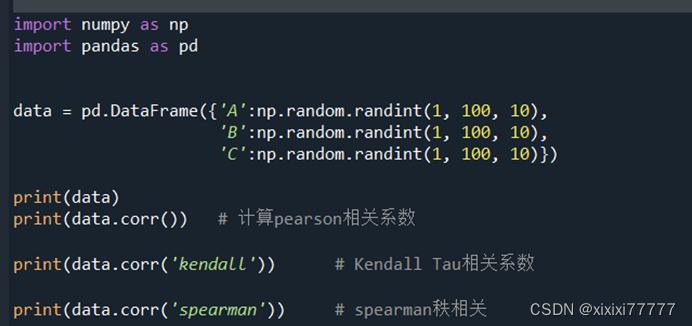
data = pd.DataFrame({'A':np.random.randint(1, 100, 10),
'B':np.random.randint(1, 100, 10),
'C':np.random.randint(1, 100, 10)})
print(data)
print(data.corr()) # 计算pearson相关系数
print(data.corr('kendall')) # Kendall Tau相关系数
print(data.corr('spearman')) # spearman秩相关
五、心得
通过这次实验,我学习了Python中Pandas库的相关数据分析方法,包括描述性统计分析、计数、求最大值、最小值、总和、均值、方差、标准差、中位数和众数等基本操作。同时,我也了解了分组分析、分布分析、交叉分析等高级分析方法。
此外,我还学习了如何使用matplotlib库绘制散点图,以及如何计算Pearson相关系数、Kendall Tau相关系数和Spearman秩相关。这些都是数据分析中非常重要的技能,尤其是相关系数的计算,可以帮助我们理解变量之间的关系。
通过实验,我明白了理论知识和实际操作的结合是非常重要的,只有动手实践,才能更好地理解和掌握知识。同时,我也意识到数据分析是一个需要细心和耐心的过程,每一步都不能马虎。



单例模式懒汉模式和饿汉模式--全局资源入口点)




![[NAND Flash 4.1] Flash(闪存)存储器底层原理 | 闪存存储器重要参数](http://pic.xiahunao.cn/[NAND Flash 4.1] Flash(闪存)存储器底层原理 | 闪存存储器重要参数)



)






