A - Three Threes

题目大意：给你一个整数n，将这个数n输出n次。

呃呃

B - Pentagon

题目大意：给你一个正五边形ABCDE，给你任意两条边，判断是否相等

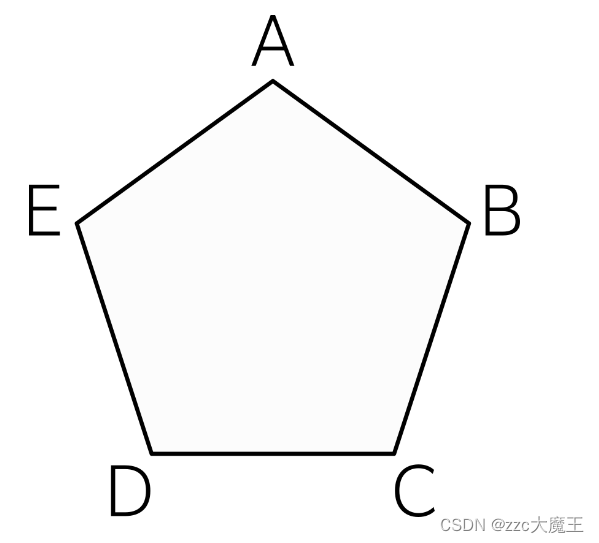
主要问题要判断一下内边：AD，AC，EB，EC，DB之间的关系，因为内边的夹角都相等，边也都相等（正五边形），所以内边都相等。要证明也可以画辅助线来证明，但是这显而易见，就不证明了。

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;string s1,s2;void yes(){cout<<"Yes"<<endl;
}
void no(){cout<<"No"<<endl;
}void solve(){cin>>s1>>s2;if(s1[1]<s1[0])swap(s1[0],s1[1]);//线段表示模式改成前面小端点后面大端点if(s2[1]<s2[0])swap(s2[0],s2[1]);//可以少判断一半if(s1=="AB" or s1=="BC" or s1=="CD" or s1=="DE" or s1=="AE"){//任意外边相等if(s2=="AB" or s2=="BC" or s2=="CD" or s2=="DE" or s2=="AE")return yes();return no();}if(s1=="AC" or s1=="AD" or s1=="BE" or s1=="CE" or s1=="BD"){//任意内边相等if(s2=="AC" or s2=="AD" or s2=="BE" or s2=="CE" or s2=="BD")return yes();return no();}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

C - Repunit Trio

题目大意：对于序列{1，11，111，1111，...}，后面类推。你可以任意选取三个相加（选取的数可以重复，但是选取的方案不能重复）来组成一个数x，对于新序列（升序）{x1，x2，x3，x4，...}，给你一个n，输出xn。

思路：因为n的范围只有333，所以可以直接暴力枚举所有相加方案，防止重复枚举开个set来存。

#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;vector<int>v;
set<int>s;
int cnt=1,n;void solve(){cin>>n;v.push_back(1);v.push_back(11);v.push_back(111);v.push_back(1111);v.push_back(11111);v.push_back(111111);v.push_back(1111111);v.push_back(11111111);v.push_back(111111111);v.push_back(1111111111);v.push_back(11111111111);v.push_back(111111111111);for(int i=0;i<v.size();++i)for(int j=0;j<v.size();++j)for(int k=0;k<v.size();++k)s.insert(v[i]+v[j]+v[k]);for(auto i:s){if(cnt==n){cout<<i;break;}cnt++;}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

D - Erase Leaves

题目大意：给你一颗树，每次你可以删去一个叶子节点，把节点1删掉至少要删掉多少个节点。

思路：因为只能删叶子节点，所以要把节点1删掉的话，要把节点1先变成叶子节点。

假设节点1的儿子有：2,3,4

那么只要删掉任意两个儿子，节点1就可以变成叶子节点了。

所以我们只需要删掉节点1周围的所有子树，然后加回最多节点数的子树即可。

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;const int N=3e5+5;
int n,u,v,f[N],maxx=INT_MIN,ans=1;//注意此处ans=1，初始化默认节点1已经被删了
vector<int>e[N];void dfs(int now,int fa){//求出每个节点下面都有多少个节点（包含自己）for(auto son:e[now])if(son!=fa){dfs(son,now);f[now]+=f[son];}
}void solve(){cin>>n;per(i,1,n-1){cin>>u>>v;e[u].push_back(v);e[v].push_back(u);}per(i,1,n)f[i]=1;//初始化为1（即包含自己）dfs(1,1);for(auto son:e[1]){//遍历节点1的儿子maxx=max(maxx,f[son]);//记录最大的子树ans+=f[son];//全部删了}cout<<ans-maxx<<endl;//加回最大的子树
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}

E - Takahashi Quest

吐槽：看到这种题目格式还以为是dp题，实际上没那么难

题目大意：高桥将会经历n个事件，每个事件可以描述为ti，xi。

如果ti=1，那么这里有一瓶xi药，可以用来对付xi怪

如果ti=2，那么这里有一个xi怪

在所有怪都被干掉的情况下，希望任意时刻高桥包里带的药的数量的最大值尽可能小。

最大值尽可能小：比如高桥可以带10瓶药来干掉5个怪，但是实际上只要5瓶药就可以了。

任意时刻：1药 1药 1怪 1药 1怪 1药，我们可以拿前面两个药来解决后面两个怪，但是这样任意时刻的最大值会变成2，然而实际上这个值为1就可以过关，每次拿一个药来干一个怪。

思路：贪心，带后悔的贪心。

因为任意时刻的最大值要尽可能小，所以我们能不带药就不带药，因为可能还会遇到怪，所以我们需要后悔前面某个不带药的时间节点，来干掉怪。

这个某个节点要尽可能选后面的，如果选前面的就会出现题目大意中说到的那个问题。

因为需要后悔，所以要保留所有药。因为尽可能要选后面的，可以开栈来维护所有药。

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;const int N=2e5+5;
int n,t[N],x[N],ans,tmp;
bool take[N];
stack<int>q[N];//q[i]={j},药效为i的药{j}void no(){cout<<-1<<endl;
}void solve(){cin>>n;per(i,1,n)cin>>t[i]>>x[i];per(i,1,n){if(t[i]==1)q[x[i]].push(i);else{if(q[x[i]].empty())return no();else{take[q[x[i]].top()]=true;q[x[i]].pop();}}}per(i,1,n){if(t[i]==1 and take[i])tmp++;else if(t[i]==2)tmp--;ans=max(ans,tmp);}cout<<ans<<endl;per(i,1,n){if(t[i]==1)cout<<take[i]<<" ";}
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}