迈入数据结构殿堂——时间复杂度和空间复杂度

一，算法效率

1.如何衡量一个算法的好坏？

2.算法效率

二，时间复杂度

1.时间复杂度的概念

2.大O的渐进表示法

3.推导大O的渐进表示法

4.常见时间复杂度举例

三，空间复杂度

一，算法效率

数据结构和算法是密不可分的，想要学好数据结构，首先我们就得从算法的效率开始。

1.如何衡量一个算法的好坏？

下面求斐波那契数列的算法好还是不好，为什么？该如何衡量一个算法的好坏呢？

public static long Fib(int N){

if(N < 3){

return 1;

}

return Fib(N-1) + Fib(N-2);

}

很多人同学可能认为衡量代码的好坏仅仅靠运行时间来评判。非也，同样的代码，使用十年前的电脑和当下流行的电脑跑出来的时间肯定相差甚远。

——所以光是掐表算时间来评判代码好坏其实并不靠谱，该情况下还取决于你的硬件能力。

要完衡量一个代码的好坏，不仅要看运行时间效率，还要看占用储存，要从时间与空间两个方向来判断。

2.算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间，在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

二，时间复杂度

1.时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个数学函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

因此，当我要计算一串代码的时间复杂度时，只需要计算该串代码基本语句被执行的次数即可。

2.大O的渐进表示法

// 请计算一下func1基本操作执行了多少次？

void func1(int N){

int count = 0;

for (int i = 0; i < N ; i++) {

for (int j = 0; j < N ; j++) {

count++;

}

}

for (int k = 0; k < 2 * N ; k++) {

count++;

}

int M = 10;

while ((M--) > 0) {

count++;

}

System.out.println(count);

}

拿到一串代码计算基本操作被执行多少次时，我们不可能去挨个数，一小串代码还好，可当我们面对一个项目的代码时，我们是不可能去挨个数出来的。

因此我们得先观察代码，找到里面被执行次数最多的那一行，上述代码被执行次数最多的很容易看出是count++；于是我们便可根据count++；循环的次数算出基本操作被执行次数了。

Func1被执行的基本操作次数：

F(N)= N*N + 2*N + 10

但当N越来越大的时候便会出现状况

• N = 10 F(N) = 130

• N = 100 F(N) = 10210

• N = 1000 F(N) = 1002010

这里我们可以类比高数中极限的思维，当N趋近于无穷大的时候，后面的常量10加不加好像对我们的时间效率并没有太大的影响，因为如今计算机的运行效率都是相当快的

如果执行简单的计算数学运算，现代CPU的速度可以达到1~10亿次每秒（1-10 GFLOPS）。
如果是执行计算机网络或系统编程等需要进行 I/O 操作的应用程序，每秒可处理约10万次命令或请求。
如果需要执行大量字符串替换、正则表达式匹配等工作，一些现代编程语言提供了 JIT 编译器或解释器，可以在每秒处理几万到数十万行文本。
如果是进行一些高性能计算等需要 GPU 和并行计算的工作，可达到每秒数十亿次计算。

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大 O 的渐进表示法。

大O 符号（ Big O notation ）：是用于描述函数渐进行为的数学符号。

3.推导大O的渐进表示法

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果是大O阶。

那么上述基本代码被执行次数就有了以下推导过程：

使用大O的渐进表示法以后，Func1的时间复杂度为：

O(N*N)

• N = 10 F(N) = 100

• N = 100 F(N) = 10000

• N = 1000 F(N) = 1000000

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)

例如：在一个长度为N数组中搜索一个数据x

最好情况：1次找到

最坏情况：N次找到

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4.常见时间复杂度举例

【实例 1 】

// 计算func2的时间复杂度？

void func2(int N) {

int count = 0;

for (int k = 0; k < 2 * N ; k++) {

count++;

}

int M = 10;

while ((M--) > 0) {

count++;

}

System.out.println(count);

}

答案：O(N)

【实例 2 】

// 计算func3的时间复杂度？

void func3(int N, int M) {

int count = 0;

for (int k = 0; k < M; k++) {

count++;

}

for (int k = 0; k < N ; k++) {

count++;

}

System.out.println(count);

}

答案：O(M+N)

【实例 3 】

// 计算func4的时间复杂度？

void func4(int N) {

int count = 0;

for (int k = 0; k < 100; k++) {

count++;

}

System.out.println(count);

}

答案：O(1)

【实例 4 】

// 计算bubbleSort的时间复杂度？

void bubbleSort(int[] array) {

for (int end = array.length; end > 0; end--) {

boolean sorted = true;

for (int i = 1; i < end; i++) {

if (array[i - 1] > array[i]) {

Swap(array, i - 1, i);

sorted = false;

}

}

if (sorted == true) {

break;

}

}

}

答案：O( $N^{2}$ )

【实例 5 】

// 计算binarySearch的时间复杂度？

int binarySearch(int[] array, int value) {

int begin = 0;

int end = array.length - 1;

while (begin <= end) {

int mid = begin + ((end-begin) / 2);

if (array[mid] < value)

begin = mid + 1;

else if (array[mid] > value)

end = mid - 1;

else

return mid;

}

return -1;

}

答案：O( $\log_{2}N$ )

【实例 6 】

// 计算阶乘递归factorial的时间复杂度？

long factorial(int N) {

return N < 2 ? N : factorial(N-1) * N;

}

答案：O(N)

【实例 7 】

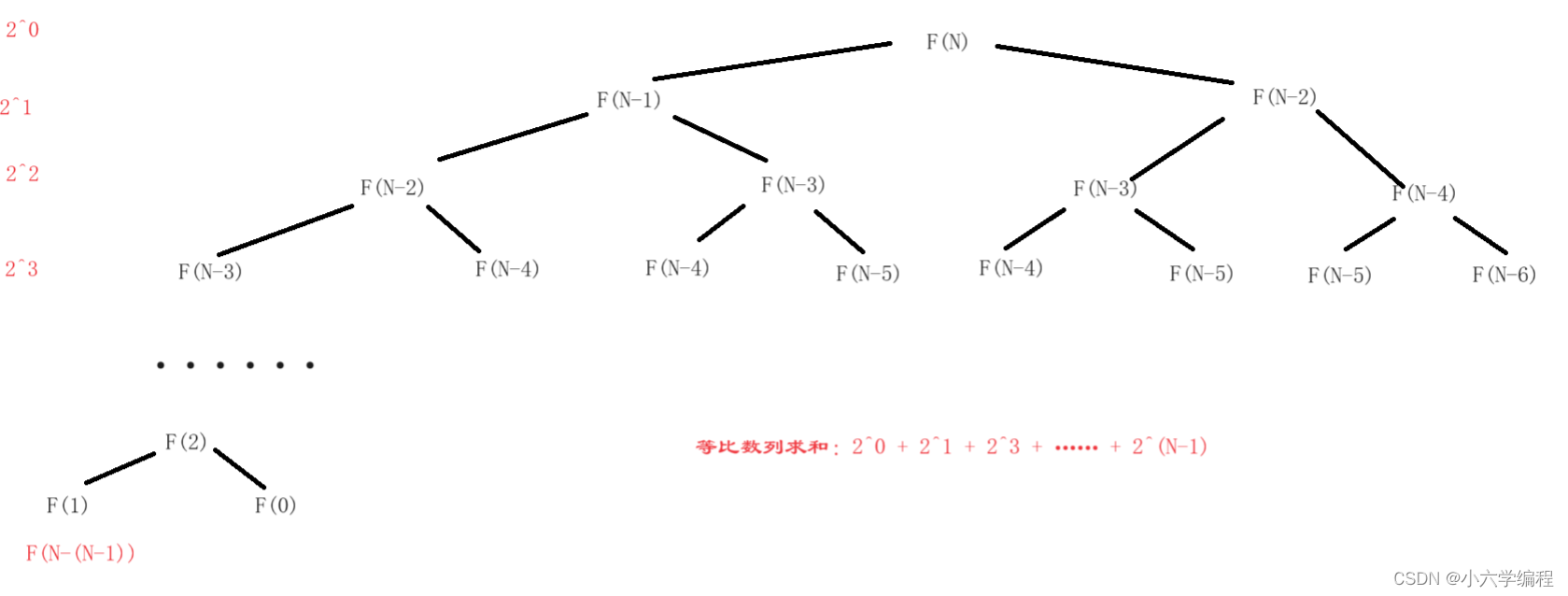
// 计算斐波那契递归fifibonacci的时间复杂度？

int fifibonacci(int N) {

return N < 2 ? N : fifibonacci(N-1)+fifibonacci(N-2);

}

答案：O( $2^{N}$ )

【实例答案及分析】

1. 实例1基本操作执行了2N+10次，通过推导大O阶方法知道，时间复杂度为 O(N)

2. 实例2基本操作执行了M+N次，有两个未知数M和N，时间复杂度为 O(N+M)

3. 实例3基本操作执行了100次，通过推导大O阶方法，时间复杂度为 O(1)

4. 实例4基本操作执行最好N次，最坏执行了(N*(N-1))/2次，通过推导大O阶方法+时间复杂度一般看最坏，时间复杂度为 O( $N^{2}$ )

5. 实例5基本操作执行最好1次，最坏 $\log_2{N}$ 次，时间复杂度为 O( $\log_{2}N$ ) ps：在算法分析中表示是底数 为2，对数为N，有些地方会写成lgN。（建议通过折纸查找的方式讲解logN是怎么计算出来的）(因为二分查找每次排除掉一半的不适合值,一次二分剩下：n/2两次二分剩下：n/2/2 = n/4)

6. 实例6通过计算分析发现基本操作递归了N次，时间复杂度为O(N)。

7. 实例7通过计算分析发现基本操作递归了 $2^{^{N}}$ 次，时间复杂度为O( $2^{N}$ )。（建议画图递归栈帧的二叉树讲解）大概会是这样的一幅图

三，空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

【实例 1 】

// 计算bubbleSort的空间复杂度？

void bubbleSort(int[] array) {

for (int end = array.length; end > 0; end--) {

boolean sorted = true;

for (int i = 1; i < end; i++) {

if (array[i - 1] > array[i]) {

Swap(array, i - 1, i);

sorted = false;

}

}

if (sorted == true) {

break;

}

}

}

答案：O(1)

【实例2】

// 计算fifibonacci的空间复杂度？

int[] fifibonacci(int n) {

long[] fifibArray = new long[n + 1];

fifibArray[0] = 0;

fifibArray[1] = 1;

for (int i = 2; i <= n ; i++) {

fifibArray[i] = fifibArray[i - 1] + fifibArray [i - 2];

}

return fifibArray;

}