1.本地事务

本地事务，也就是传统的单机事务。在传统数据库事务中，必须要满足四个原则：

2.分布式事务

分布式事务，就是指不是在单个服务或单个数据库架构下，产生的事务，例如：

• 跨数据源的分布式事务

• 跨服务的分布式事务

• 综合情况

        在数据库水平拆分、服务垂直拆分之后，一个业务操作通常要跨多个数据库、服务才能完成。例如电商行业中比较常见的下单付款案例，包括下面几个行为：

• 创建新订单

• 扣减商品库存

• 从用户账户余额扣除金额

完成上面的操作需要访问三个不同的微服务和三个不同的数据库。

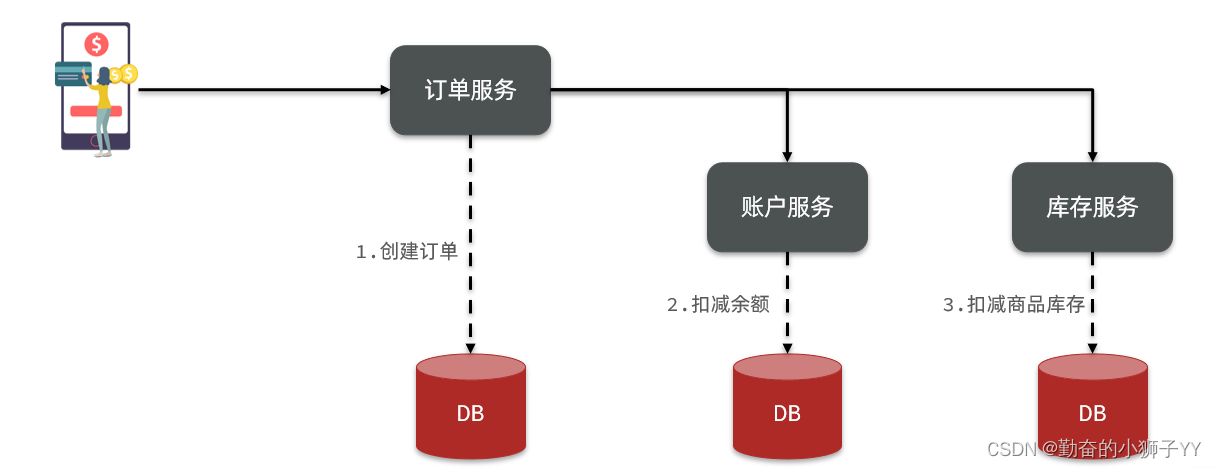
        订单的创建、库存的扣减、账户扣款在每一个服务和数据库内是一个本地事务，可以保证ACID原则。

        但是当我们把三件事情看做一个"业务"，要满足保证“业务”的原子性，要么所有操作全部成功，要么全部失败，不允许出现部分成功部分失败的现象，这就是分布式系统下的事务了。

        此时ACID难以满足，这是分布式事务要解决的问题

1.3.演示分布式事务问题

我们通过一个案例来演示分布式事务的问题：

1）创建数据库，名为seata_demo，然后导入SQL文件：

链接：https://pan.baidu.com/s/10bd7RX9lXqIDlMODMOyV4Q?pwd=3l4o 
提取码：3l4o 
--来自百度网盘超级会员V6的分享

2）导入微服务：

链接：https://pan.baidu.com/s/1tB_c5KbskqGfFLP-phC0dQ?pwd=tgvp 
提取码：tgvp 
--来自百度网盘超级会员V6的分享

微服务结构如下：

其中：

seata-demo：父工程，负责管理项目依赖

• account-service：账户服务，负责管理用户的资金账户。提供扣减余额的接口

• storage-service：库存服务，负责管理商品库存。提供扣减库存的接口

• order-service：订单服务，负责管理订单。创建订单时，需要调用account-service和storage-service

3）启动nacos、所有微服务

4）测试下单功能，发出Post请求：

测试发现，当库存不足时，如果余额已经扣减，并不会回滚，出现了分布式事务问题。(各个分支事务之间互相感知不到，各提交各的，因此无法回滚)

3.理论基础

解决分布式事务问题，需要一些分布式系统的基础知识作为理论指导。

3.1.CAP定理

1998年，加州大学的计算机科学家 Eric Brewer 提出，分布式系统有三个指标。

• Consistency（一致性）

• Availability（可用性）

• Partition tolerance （分区容错性）

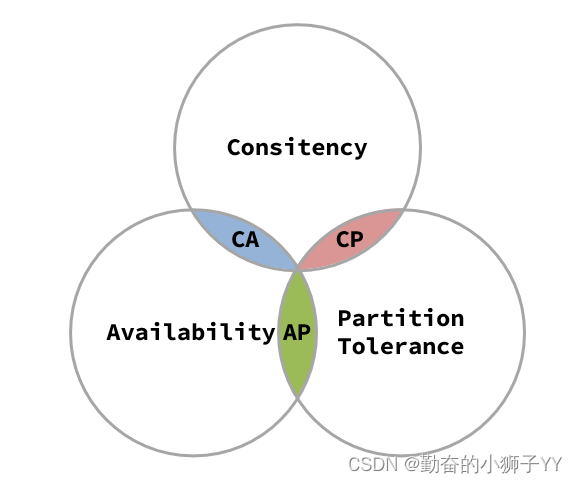
它们的第一个字母分别是 C、A、P。

Eric Brewer 说，这三个指标不可能同时做到（最多同时满足两个）。这个结论就叫做 CAP 定理。

3.1.1.一致性

Consistency（一致性）：用户访问分布式系统中的任意节点，得到的数据必须一致。

比如现在包含两个节点，其中的初始数据是一致的：

 当我们修改其中一个节点的数据时，两者的数据产生了差异：

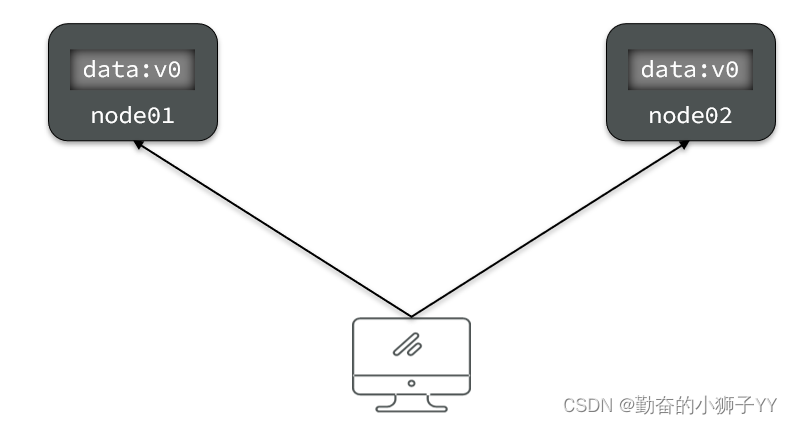
 要想保住一致性，就必须实现node01 到 node02的数据 同步：

3.1.2.可用性

Availability （可用性）：用户访问集群中的任意健康节点，必须能得到响应，而不是超时或拒绝。

如图，有三个节点的集群，访问任何一个都可以及时得到响应：

 当有部分节点因为网络故障或其它原因无法访问时，代表节点不可用：

3.1.3.分区容错

Partition（分区）：因为网络故障或其它原因导致分布式系统中的部分节点与其它节点失去连接，形成独立分区。

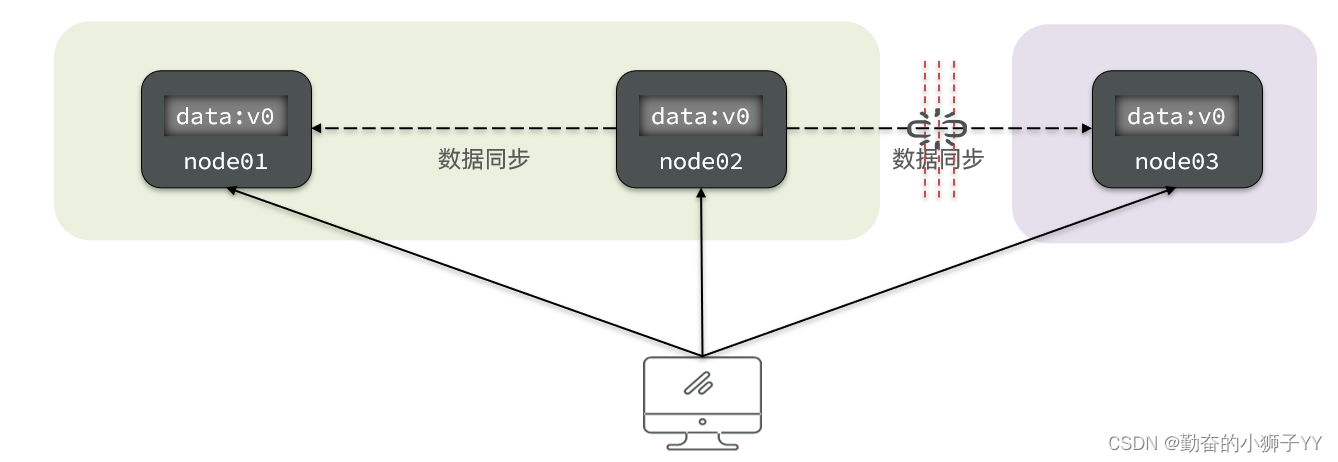
Tolerance（容错）：在集群出现分区时，整个系统也要持续对外提供服务

3.1.4.矛盾

在分布式系统中，系统间的网络不能100%保证健康，一定会有故障的时候，而服务有必须对外保证服务。因此Partition Tolerance不可避免。

当节点接收到新的数据变更时，就会出现问题了：

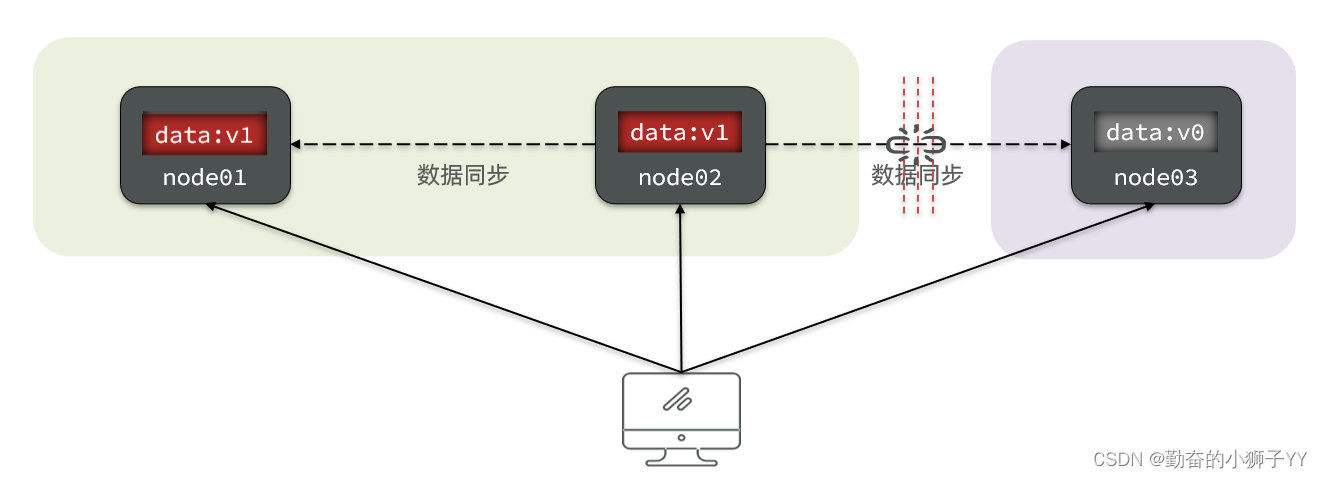
如果此时要保证一致性，就必须等待网络恢复，完成数据同步后，整个集群才对外提供服务，服务处于阻塞状态，不可用。

如果此时要保证可用性，就不能等待网络恢复，那node01、node02与node03之间就会出现数据不一致。

也就是说，在P一定会出现的情况下，A和C之间只能实现一个。

3.2.BASE理论（调和矛盾）

BASE理论是对CAP的一种解决思路，包含三个思想：

• Basically Available （基本可用）：分布式系统在出现故障时，允许损失部分可用性，即保证核心可用。

• Soft State（软状态）：在一定时间内，允许出现中间状态，比如临时的不一致状态。

• Eventually Consistent（最终一致性）：虽然无法保证强一致性，但是在软状态结束后，最终达到数据一致。

4.解决分布式事务的思路

分布式事务最大的问题是各个子事务的一致性问题，因此可以借鉴CAP定理和BASE理论，有两种解决思路：

• AP模式：各子事务分别执行和提交，允许出现结果不一致，然后采用弥补措施恢复数据即可，实现最终一致。

• CP模式：各个子事务执行后互相等待，同时提交，同时回滚，达成强一致。但事务等待过程中，处于弱可用状态。

但不管是哪一种模式，都需要在子系统事务之间互相通讯，协调事务状态，也就是需要一个事务协调者(TC)

这里的子系统事务，称为分支事务；有关联的各个分支事务在一起称为全局事务。

喜欢的话友友们点个关注吧！