这道题和前一天的射箭题目思想类似，用总区间个数-不重叠的区间个数等于需要去除的区间个数。首先对左边界排序，如果当前的左边界大于等于上一区间的右边界，则说明是一个不重叠的区间，否则，更新上一重叠区间的最小右边界，详细代码如下：

class Solution {
public:static bool cmp(vector<int>&a, vector<int>&b){return a[0]<b[0];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {//类似射箭if(intervals.size()==1) return 0;sort(intervals.begin(),intervals.end(),cmp);int sum = 1;for(int i=1;i<intervals.size();i++){if(intervals[i][0]>=intervals[i-1][1]){sum++;}else{intervals[i][1] = min(intervals[i][1],intervals[i-1][1]);}}return intervals.size()-sum;}
};

763.划分字母区间 

这道题的思路很巧妙，首先记录每个字符最后出现的位置，然后从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点，如图：

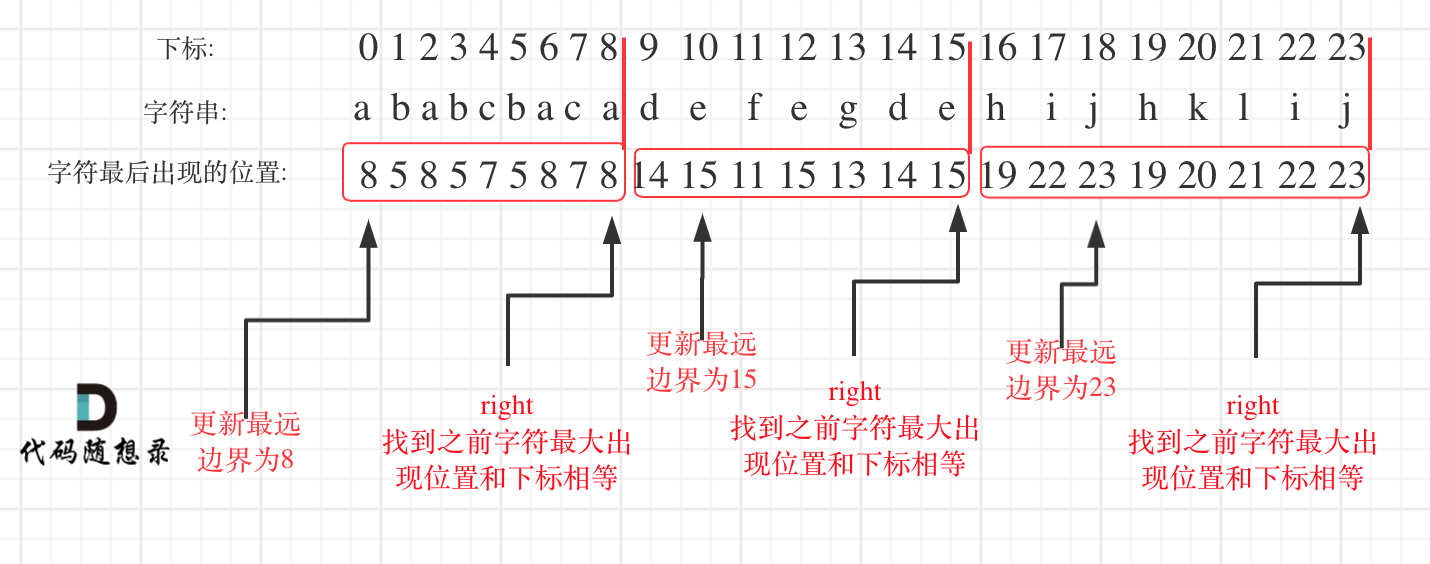
详细代码如下：

class Solution {
public:vector<int> partitionLabels(string s) {int hash[27] = {0};for(int i=0;i<s.size();i++) //记录最后出现的位置{hash[s[i]-'a']= i;}vector<int> res;int right=0;int left = 0;for(int i =0;i<s.size();i++){right = max(right,hash[s[i]-'a']);if(i==right){res.push_back(right-left+1);left=i+1;}}return res;}
};

56. 合并区间  

这道题目和之前的重叠区间思路相似，也是先左边界排序，然后再判断是否重叠，不重叠直接添加元素，重叠的话则需要更新右边界，（左边界一定是最小的，无需更新），详细代码如下：

class Solution {
public:static bool cmp(vector<int>&a, vector<int>&b){return a[0]<b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {if(intervals.size()==1) return intervals;sort(intervals.begin(),intervals.end(),cmp);vector<vector<int>> res;res.push_back(intervals[0]); //先加入元素for(int i = 1;i<intervals.size();i++){if(intervals[i][0]>res.back()[1]) //不重叠{res.push_back(intervals[i]); //不重叠，直接添加元素}else //重叠{//更新右边界，左一定最小res.back()[1] = max(res.back()[1], intervals[i][1]); }}return res;}
};