目录
算数类型和基本数据类型
基数
基数转换
由八进制数、十六进制数、二进制数向十进制数转换
由十进制数向八进制数、十六进制数、二进制数转换
二进制和十六进制的基数转换
在学习基本数据类型之前我们先来学习数。
算数类型和基本数据类型
在前面的学习中我们可以使用int型double型的变量及常量进行加减等算数运算,这种数据类型称为算数类型(arithmetic type)。算数类型是多种数据类型的统称,大体上分为两种类型:
整数类数据类型(integral type):只表示整数
浮点型类(floating type):可表示具有小数部分的数值。
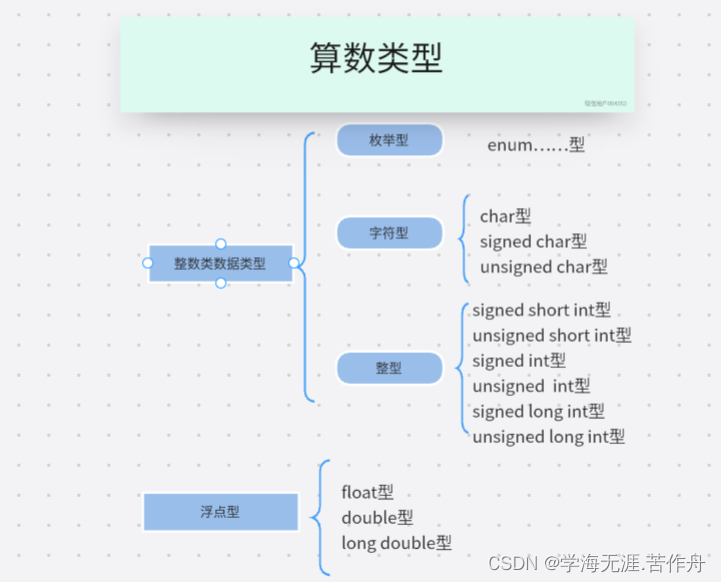
整数类型数据是以下数据类型的统称:
枚举型:下一节将会介绍
字符型:表示字符
整型:表示整数
字符型、整形和浮点型只需要使用int或double等关键字就能表示其他数据类型,因此将它们统称为基本数据类型(basic type)
基数
先来学习整数:我的二伯出生于1963年,这种数值很常见,是以10为基数的十进制数。
在表示数值时,基数是进位的标准。基数为10的十进制数每逢10或10的倍数进位。
十进制数是我们日常生活中用到的,但对于计算机,所有的数据都是用NO/OFF信号(1和0)表示的。
就接近底层的硬件程序来说,使用二进制数更加适宜,但也存在位数过多的缺点,所以写法上还存在八进制数与十六进制数。
在十进制数中,如果以下10中数字都用完了,就进位为10
0 1 2 3 4 5 6 7 8 9
如果两位的10—99也用完了,就进位为100
在八进制中用完以下8种数字后就进位为10
0 1 2 3 4 5 6 7
如果两位的10—77也用完的话,就进位为100
在十六进制数中用完以下16种数字后,F后面的数就是10
0 1 2 3 4 5 6 7 8 9 A B C D E F
如果10—FF也用完了,还会再进一位,变为100
如下所示,用0—20分别用八进制、十进制、十六进制数表示:
八进制数:0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 24
十进制数:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
十六进制数:0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14
二进制只使用0和1两种数字进行表示数值,十进制的0—13用二进制表示就是:
0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101
基数转换
下面我们学习不同基数间的整数值的相互转换方法
由八进制数、十六进制数、二进制数向十进制数转换
十进制数的每一位都是10的指数幂,所以1998可以理解为:
1998=1*10^3+9*10^2+9*10^1+8*10^0
将这个思路转换到八进制数、十六进制数、二进制数上就能轻松将这些数据转换为10进制数
举例说明:将八进制数123转化为十进制数

将十六进制数1FD转换为十进制数
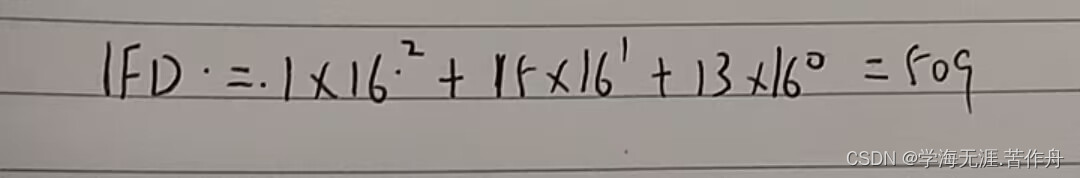
将二进制数101转换为十进制数
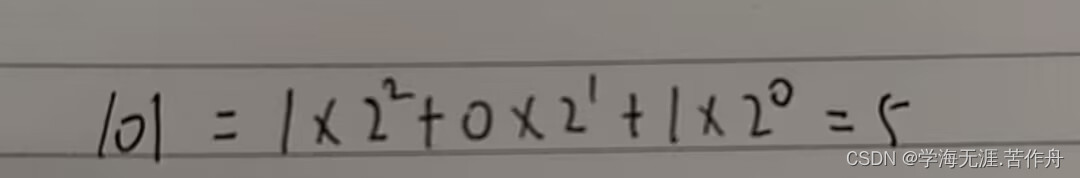
由十进制数向八进制数、十六进制数、二进制数转换
二进制数有以下规律:
偶数的末位数字为0
基数的末尾数字为1
也就是说,用转化的数除以2所得到的余数就是末位数字的值
例如,十进制数57除以2的余数为1,那么转换为二进制数的末位数字就是1.
我们先对“十进制数转换为十进制数”的方法进行说明,一个数除以10的余数,与这个数的末尾数字相等,例如1962除以10的余数为2,得到196,再除以10余数为6,得到19,再除以10余数为9,得到1,再除以10时,余数为1,商为0停止。
最后将所得到的余数进行逆向排列就可以得到转换后的十进制数。
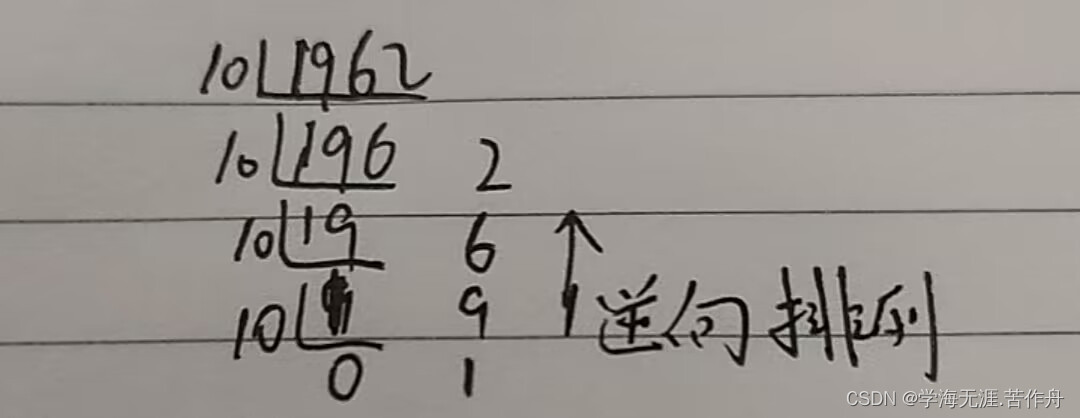
将10改为2,就是十进制数转换为二进制数的方法了,现在我们用十进制数57转化为二进制数

对于八进制数、与十六进制数也是一样,只是把除数换为8和16而已
例如将57转化为八进制数为71,转化为十六进制数为39
二进制和十六进制的基数转换
| 二进制数 十六进制数 二进制数 十六进制数 0000 0 1000 8 0001 2 1001 9 0010 3 1010 A 0011 4 1011 B 0100 5 1100 C 0101 6 1101 D 0110 7 1110 E 0111 8 1111 F 4位二进制数和1位十六进制数是相互对应的 当我们需要将二进制数转换为十六进制数时,只需每隔开四位,分别转换为1位的十六进制数,从右到左划分,奇数位补0变位4位。 要将十六进制数转换为二进制数,只需反过来操作即可。 |










)








