目录
一、散列查找结构思路图
二、哈希函数
三、解决冲突
1.开放地址法
1.1.线性探测法(线性探测再散列法)
1.2.平方探测法(二次探测再散列)
1.3.再散列法(双散列法)
2.拉链法
2.1简介
四、散列查找性能
4.1.散列查找
4.2.装填因子
4.2.1关于装填因子的平均昌曌长度的计算。
4.3.查找成功的平均查找长度。
4.3.1.开放地址法-查找成功
4.3.2.拉链法-查找成功
4.4.查找失败的平均查找长度
4.4.1.开放地址法-查找失败
4.4.1.拉链法-查找失败
一、散列查找结构思路图

二、哈希函数
简介:把查找表中的关键字映射成该关键字对应的地址的函数,记为Hash(key)=Addr.即通过哈希函数的公式计算,得到关键字地址。其中哈希函数分为五种,选择一种即可。具体看一中的思路图。
这里面主要说明除留余数法,这里考试考察,公式为Hash(key)=key%p,p为数组中最大素数,key为关键字。如图,

通过哈希函数的除留余数法,计算关键字在数组中的坐标,从而填在相应的位置下。
三、解决冲突
1.开放地址法
简介:即数组中位置,即向相同位置的关键字开放,也对不同的开放。
1.1.线性探测法(线性探测再散列法)
Hash(key)=(key+di)%p.其中di=1,2,3,4,5,6.......
直接看图-强连通例题

当关键字37时,通过除留余数法,发现冲突,此时,需要用到线性探测法即,H1=(H(37)+1)%12,这里H(37)为除留余数法初始坐标。从而算出新的地址,如果此时不冲突则填进去,否则再进行计算H2=(H(37)+2)%12,直到不冲突位置。此外,如果在散列表中,删除关键字,只能逻辑删除,物理删除的话,会造成后续关键字映射紊乱。
此外,若有k个关键字,弄成散列表,则需要k*(k+1)/2次对比。第一个1次。第二个2次。以此类推,等差数列。
1.2.平方探测法(二次探测再散列)

相比于线性探测而言,它的di不同,di为(1,-1,2,-2,4,-4)
例题:

45先是通过除留余数法计算,发现6,冲突了,从而进行第一次冲突计算,此时di=1,带进公式计算即可,如果还冲突,则di更新为-1,注意H(45)=6这个初始位置不变,跟着di带进公式即可。
1.3.再散列法(双散列法)
即先通过除留余数法计算,如果地址冲突了,再通过第二个函数式子,进行位置计算,一般不同题中给的再散列函数不一样,不过按照所给的条件,带入计算即可。
例题:


简单来说,就是分两步,先是通过正常的除留余数法进行计算地址,如果,发生冲突,则通过题干中给的第二个函数,进行新地址的计算。
2.拉链法
2.1简介
拉链法,为了避免开放地址法中的聚集现象,以及插入删除不方便等情况应运而生。
直接看图吧,相比于开放定址法,这里处理冲突的方法,则是,通过除留余数法,所求的相同的地址,都放在一个单链表中,那么此时该地址的链,为同义词所在的链。

四、散列查找性能
4.1.散列查找
即我们构造完散列表了,然后通过关键则,获取在表中的位置。先通过哈希函数hash(key)=key%p=addr,获取初始位置,如果此时L(addr)==key则返回addr即可,否则addr+1,往后查找,验证l(addr+1)==key?直到符合条件,返回此时的位置即可。

4.2.装填因子
一般记为a,表示表中装满程度,a=表中记录关键字数/表长度。
a越大,说明此时表中填充的越多,下次再加入关键字冲突的可能性就越大。
4.2.1关于装填因子的平均昌曌长度的计算。

4.3.查找成功的平均查找长度。
4.3.1.开放地址法-查找成功
即每个关键字比较次数总和/关键字总数。比较次数即冲突数+1.在构造散列表的时候,顺便就计算了,

4.3.2.拉链法-查找成功
直接看图好理解。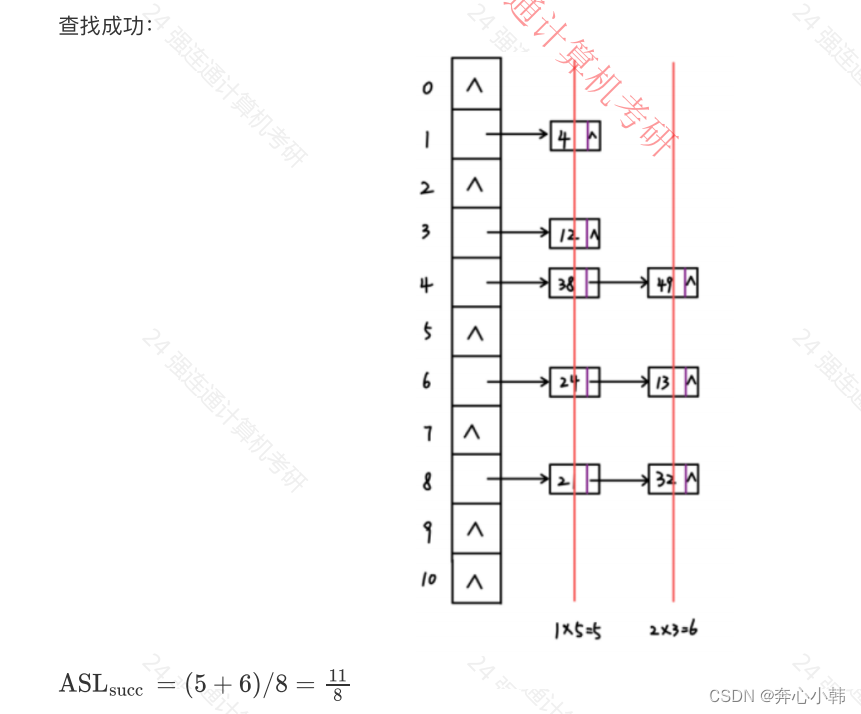
4.4.查找失败的平均查找长度
4.4.1.开放地址法-查找失败
这里先需要直到映射地址的范围,即除留余数法中的key%p的p,这个为范围。然后从范围第一个位置,查找,直到后面遇到空白才听,空白也算一次查找失败,这是一个位置的查找失败,然后从左到右,依次计算,直到映射地址计算完毕,
注意如果散列表中,删除关键字,则为逻辑删除,但是在进行查找长度计算时,它仍物理存在,计算的时候要算上。

删除关键字后的查找失败的平均查找长度

4.4.1.拉链法-查找失败

即,散列表中空白处算1次查找失败,有链表的地方,为链表长度+1,因为后面的空指针,也算一次比较。
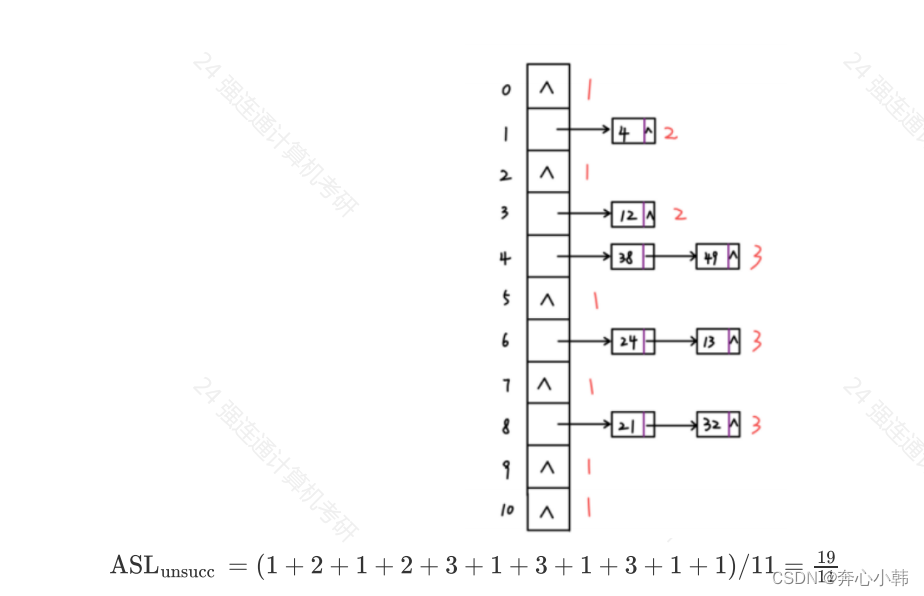



)
)


)




)
)





