239. 滑动窗口最大值
单调队列
滑动窗口中的队列一直保持出口大,入口小的顺序。(图:代码随想录)
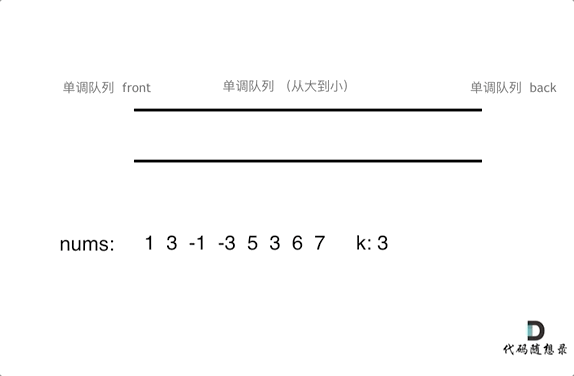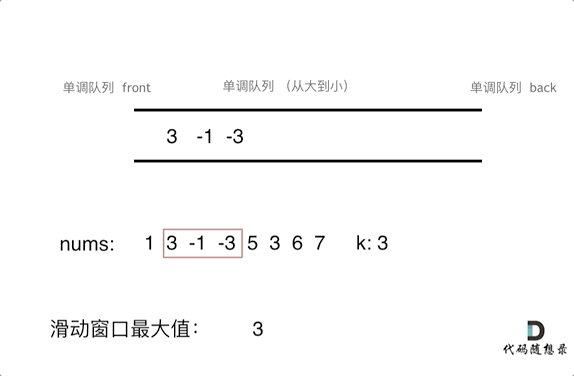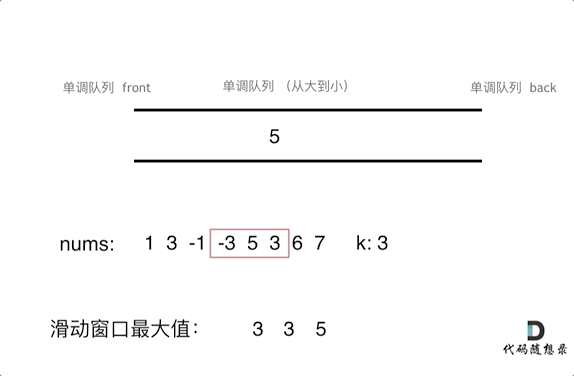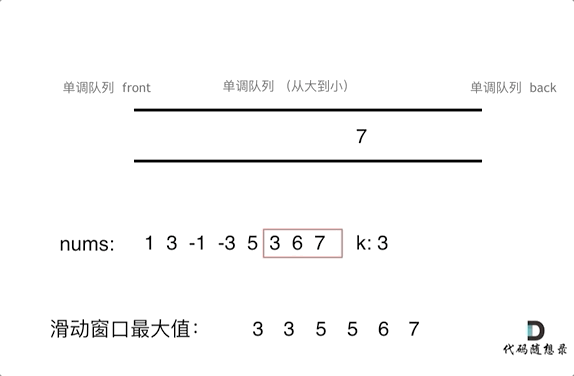
1、每次有新的元素进入(也就是滑动窗口移动后),都需要先和入口的元素比较大小,如果大,就从队尾pop出之前的元素(双向队列的特性),如果小,则保留。
2、每次需要pop队列头部的元素,需要先和当前队列的头部元素比较,只pop滑动窗口即将舍弃的值。
from collections import dequeclass MyQueue:"""双向队列dequeue始终保持队列头部pop()为最大值,尾部push()为最小值pop<-- [0] [1] [-1] <--pushmax mid min"""def __init__(self):self.queue = deque()def pop(self, value):# 如果队列非空而且需要pop的值恰好就是队头的数值if self.queue and value == self.queue[0]:self.queue.popleft()def push(self, value):# 如果队列非空,而且需要push进入的值比队尾的值都大,那么队尾就一直pop出去while self.queue and value > self.queue[-1]:self.queue.pop()self.queue.append(value)def getMax(self):# 始终保持头部是最大值,返回队列头部就是最大值return self.queue[0]class Solution(object):def maxSlidingWindow(self, nums, k):""":type nums: List[int]:type k: int:rtype: List[int]"""queue = MyQueue()ans = []# 先储存前k个数值,保证队列非空for i in range(k):queue.push(nums[i])ans.append(queue.getMax())# 然后遍历nums数组for i in range(k, len(nums)):queue.pop(nums[i - k])queue.push(nums[i])ans.append(queue.getMax())return ans347. 前 K 个高频元素
大顶堆:根节点是最大值,先pop的是最大值;
小顶堆:根节点是最小值,先pop的是最小值。
所以只需要按照出现频率排序放入小顶堆,然后pop直到还剩k个元素,再按照倒序输出即可。
优先级队列法
1、首先遍历数组建立map键值对;
2、建立小顶堆,按照从大到小的顺序放入键值对,当队列的长度大于k的时候,开始从最小值节点pop元素,留下k个最大值;
3、倒序输出最大值对应的key即可。
class Solution(object):def topKFrequent(self, nums, k):""":type nums: List[int]:type k: int:rtype: List[int]"""# 获取键值对map_freq = {} # (key, value) = ('a', 4), ('b', 3) ...for item in nums:map_freq[item] = map_freq.get(item, 0) + 1 # 注意get写法# 构造小顶堆prime_que = [] # 创建优先级队列(这里是小顶堆)"""heapq用法:heapq.heappush()是往堆中添加新值heapq.heappop()是从堆的根节点弹出值,大顶堆弹出最大值,小顶堆弹出最小值"""for key, value in map_freq.items():heapq.heappush(prime_que, (value, key)) # 先入的是最大值if len(prime_que) > k:heapq.heappop(prime_que)res = [0] * k# 倒序输出for i in range(k-1, -1, -1):res[i] = heapq.heappop(prime_que)[1]return res注意构造小顶堆的方式:heapq
heapq用法:
heapq.heappush()是往堆中添加新值
heapq.heappop()是从堆的根节点弹出值,大顶堆弹出最大值,小顶堆弹出最小值
第13天完结🎉




含训练代码)









)

搭建项目)


