一、Softmax回归关键思想

1、回归问题和分类问题的区别

       Softmax回归虽然叫“回归”，但是它本质是一个分类问题。回归是估计一个连续值，而分类是预测一个离散类别。

2、Softmax回归模型

       Softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，Softmax回归的输出值个数等于标签里的类别数。比如一共有4种特征和3种输出动物类别(猫、狗、猪），则权重包含12个标量（带下标的），偏差包含3个标量（带下标的），且对每个输入计算这三个输出：

最后，再对这些输出值进行Softmax函数运算。

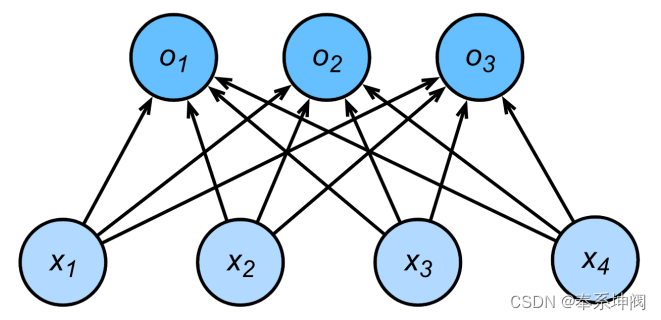
       softmax回归同线性回归一样，也是一个单层神经网络。由于每个输出的计算都要依赖于所有的输入，所以softmax回归的输出层也是一个全连接层。

3、Softmax函数

       Softmax用于多分类过程中，它将多个神经元的输出（比如）映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！它通过下式将输出值变换成值为正且和为1的概率分布：

其中：

， ， 

       容易看出  且 ，因此  是一个合法的概率分布。此外，我们注意到：

 因此softmax运算不改变预测类别输出。

       下图可以更好的理解Softmax函数，其实就是取自然常数e的指数相加后算比例，由于自然常数的指数（）在单调递增，因此softmax运算不改变预测类别输出。

4、交叉熵损失函数

       假设我们希望根据图片动物的轮廓、颜色等特征，来预测动物的类别，有三种可预测类别：猫、狗、猪。假设我们当前有两个模型（参数不同），这两个模型都是通过sigmoid/softmax的方式得到对于每个预测结果的概率值：

模型1：

模型1
预测			真实				是否正确
0.3	0.3	0.4	0	0	1	猪	正确
0.3	0.4	0.3	0	1	0	狗	正确
0.1	0.2	0.7	1	0	0	猫	错误

       模型评价：模型1对于样本1和样本2以非常微弱的优势判断正确，对于样本3的判断则彻底错误。

模型2：

模型2
预测			真实				是否正确
0.1	0.2	0.7	0	0	1	猪	正确
0.1	0.7	0.2	0	1	0	狗	正确
0.3	0.4	0.3	1	0	0	猫	错误

       模型评价：模型2对于样本1和样本2判断非常准确，对于样本3判断错误，但是相对来说没有错得太离谱。

       好了，有了模型之后，我们需要通过定义损失函数来判断模型在样本上的表现了，那么我们可以定义哪些损失函数呢？我们可以先尝试使用以下几种损失函数，然后讨论哪种效果更好。

（1）Classification Error（分类错误率）

       最为直接的损失函数定义为：

模型1：

模型2：

       我们知道，模型1和模型2虽然都是预测错了1个，但是相对来说模型2表现得更好，损失函数值照理来说应该更小，但是，很遗憾的是，classification error 并不能判断出来，所以这种损失函数虽然好理解，但表现不太好。

（2）Mean Squared Error（均方误差MSE）

       均方误差损失也是一种比较常见的损失函数，其定义为：

模型1：

对所有样本的loss求平均：

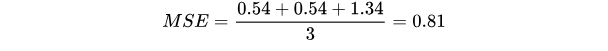
模型2：

对所有样本的loss求平均：

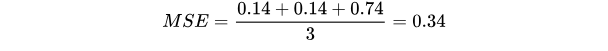
       我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？主要原因是在分类问题中，使用sigmoid/softmx得到概率，配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况（损失函数 | Mean-Squared Loss - 知乎）。

       有了上面的直观分析，我们可以清楚的看到，对于分类问题的损失函数来说，分类错误率和均方误差损失都不是很好的损失函数，下面我们来看一下交叉熵损失函数的表现情况。

（3）Cross Entropy Loss Function（交叉熵损失函数）

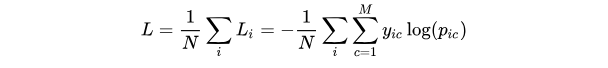
其中：

：类别的数量

：符号函数（0或1），如果样本 i 的真实类别等于 c 取 1，否则取 0

：观测样本 i 属于类别 c 的预测概率

：样本的数量

现在我们利用这个表达式计算上面例子中的损失函数值：

模型1：

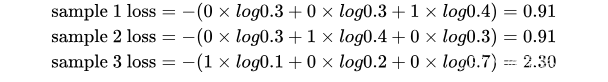
对所有样本的loss求平均：

模型2：

对所有样本的loss求平均：

       可以发现，交叉熵损失函数可以捕捉到模型1和模型2预测效果的差异，因此对于Softmax回归问题我们常用交叉熵损失函数。

      下面两图可以很清晰的反应整个Softmax回归算法的流程：

二、图像分类数据集

       MNIST数据集是图像分类中广泛使用的数据集之一，但作为基准数据集过于简单。我们将使用类似但更复杂的Fashion-MNIST数据集。

       在这里我们定义一些函数用于数据的读取与显示，这些函数已经在Python包d2l中定义好了，但为了便于大家理解，这里没有直接调用d2l中的函数。

1、读取数据集

       我们可以通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中。

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)

       Fashion-MNIST由10个类别的图像组成，每个类别由训练数据集（train dataset）中的6000张图像和测试数据集（test dataset）中的1000张图像组成。因此，训练集和测试集分别包含60000和10000张图像。测试数据集不会用于训练，只用于评估模型性能。

print(len(mnist_train), len(mnist_test))

60000 10000

       每个输入图像的高度和宽度均为28像素。数据集由灰度图像组成，其通道数为1。为了简洁起见，本书将高度像素、宽度像素图像的形状记为或。接下来我们可以打印一下mnist_train的类型和mnist_train的第一个元素。

print(type(mnist_train))
print(type(mnist_train[0]))
print(mnist_train[0])
print(mnist_train[0][0].shape)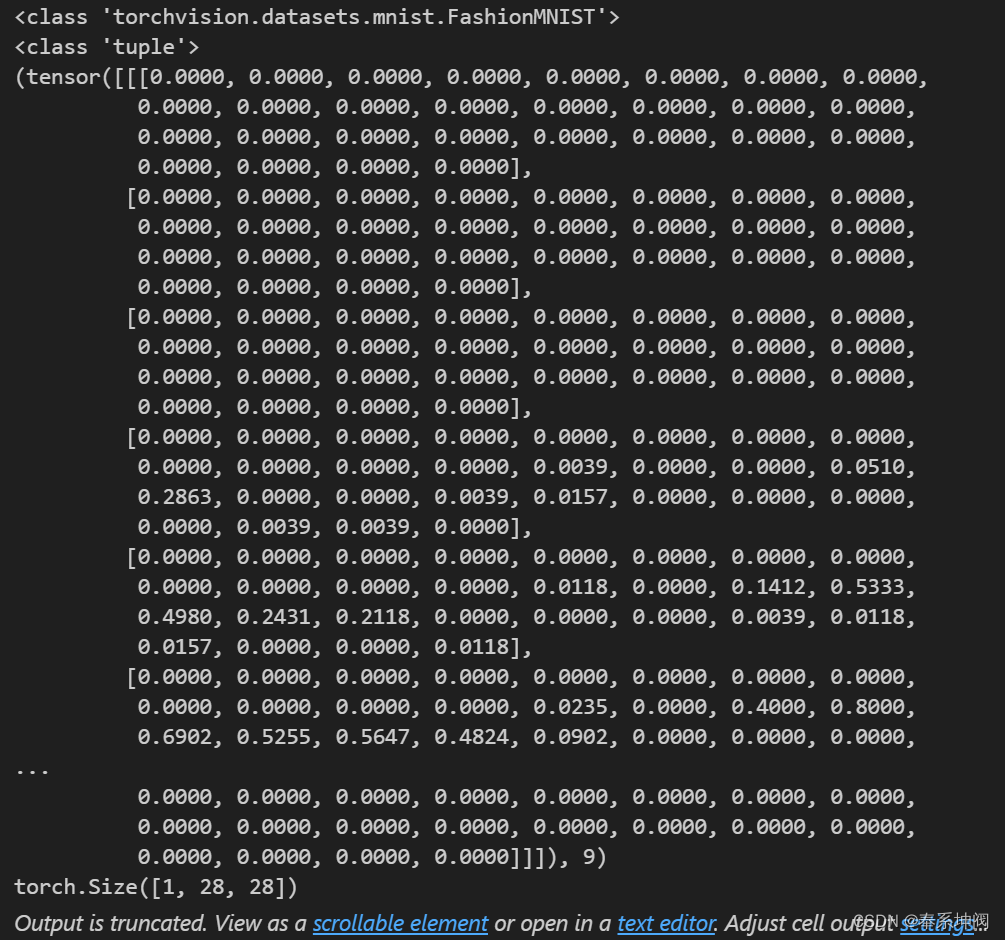

       可以看出mnist_train的类型为<class 'torchvision.datasets.mnist.FashionMNIST'>。mnist_train的第一个元素的类型是<class 'tuple'>，是一个元组，元组第一个元素是转化为tensor后的灰度值，第二个元素是图像所属类别index，这里是9。因为是灰度图，因此channel数量为1，图片长和宽都是28，因此形状是(1,28,28)。

       Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。

       以下函数用于在数字标签索引及其文本名称之间进行转换。

def get_fashion_mnist_labels(labels):   # labels:mnist_train和mnist_test里面图像的类别index(数字)"""返回Fashion-MNIST数据集的文本标签"""text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat','sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']return [text_labels[int(i)] for i in labels]    # 根据index返回文本标签列表('t-shirt', 'trouser'...)

       我们现在可以创建一个函数来可视化这些样本。

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save"""绘制图像列表""""""imgs: tensor向量num_rows: 画图时的行数num_cols: 画图时的列数titles: 每张图片的标题scales: 因为要将num_rows*num_cols张图片画到一张图上,并且还要添加一些文字,因此需要对大图进行一定的缩放才能保证每张小图之间的间隙"""figsize = (num_cols * scale, num_rows * scale)# figsize = (num_cols, num_rows)_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)axes = axes.flatten()for i, (ax, img) in enumerate(zip(axes, imgs)):if torch.is_tensor(img):# 图片张量ax.imshow(img.numpy())else:# PIL图片ax.imshow(img)ax.axes.get_xaxis().set_visible(False)ax.axes.get_yaxis().set_visible(False)if titles:ax.set_title(titles[i])return axes

       以下是训练数据集中前18个样本的图像及其相应的标签。

X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))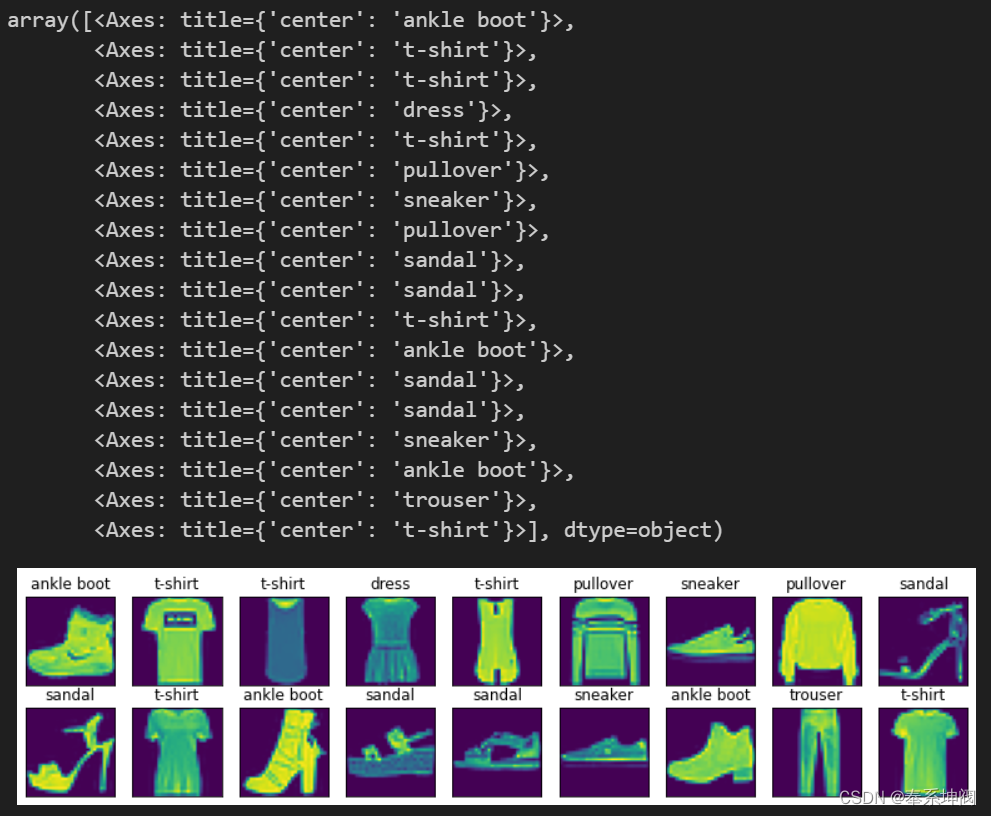

2、读取小批量数据

       为了使我们在读取训练集和测试集时更容易，我们使用内置的数据迭代器，而不是从零开始创建。在每次迭代中，数据加载器每次都会读取一小批量数据，大小为`batch_size`。通过内置数据迭代器，我们可以随机打乱所有样本，从而无偏见地读取小批量。

batch_size = 256def get_dataloader_workers():  #@save"""使用4个进程来读取数据"""return 4train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers())

3、整合所有组件

       现在我们定义`load_data_fashion_mnist`函数，用于获取和读取Fashion-MNIST数据集。这个函数返回训练集和验证集的数据迭代器。此外，这个函数还接受一个可选参数`resize`，用来将图像大小调整为另一种形状。

def load_data_fashion_mnist(batch_size, resize=None):"""下载Fashion-MNIST数据集，然后将其加载到内存中"""trans = [transforms.ToTensor()]    # 此时的trans是一个列表if resize:trans.insert(0, transforms.Resize(resize))    # 如果提供了resize参数，则在转换链中插入Resize操作trans = transforms.Compose(trans)    # 将一系列的图像转换操作组合成一个转换链。# trans是一个由多个图像转换操作组成的列表。它按照列表中的顺序依次应用这些转换操作。# 这样可以将多个转换操作组合在一起，以便在加载数据时一次性应用它们。mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)return (data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers()),data.DataLoader(mnist_test, batch_size, shuffle=False,num_workers=get_dataloader_workers()))

       下面，我们通过指定`resize`参数来测试`load_data_fashion_mnist`函数的图像大小调整功能。

train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:print(X.shape, X.dtype, y.shape, y.dtype)break

torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64

三、softmax回归的从零开始实现

...

参考文献

[1]  损失函数｜交叉熵损失函数

[2]  深度学习模型系列一——多分类模型——Softmax 回归-CSDN博客

[3]  Softmax 回归_哔哩哔哩_bilibili