学习目标：

动态规划五部曲：
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录！

本文大多数内容引用自代码随想录

60天训练营打卡计划！

学习内容：

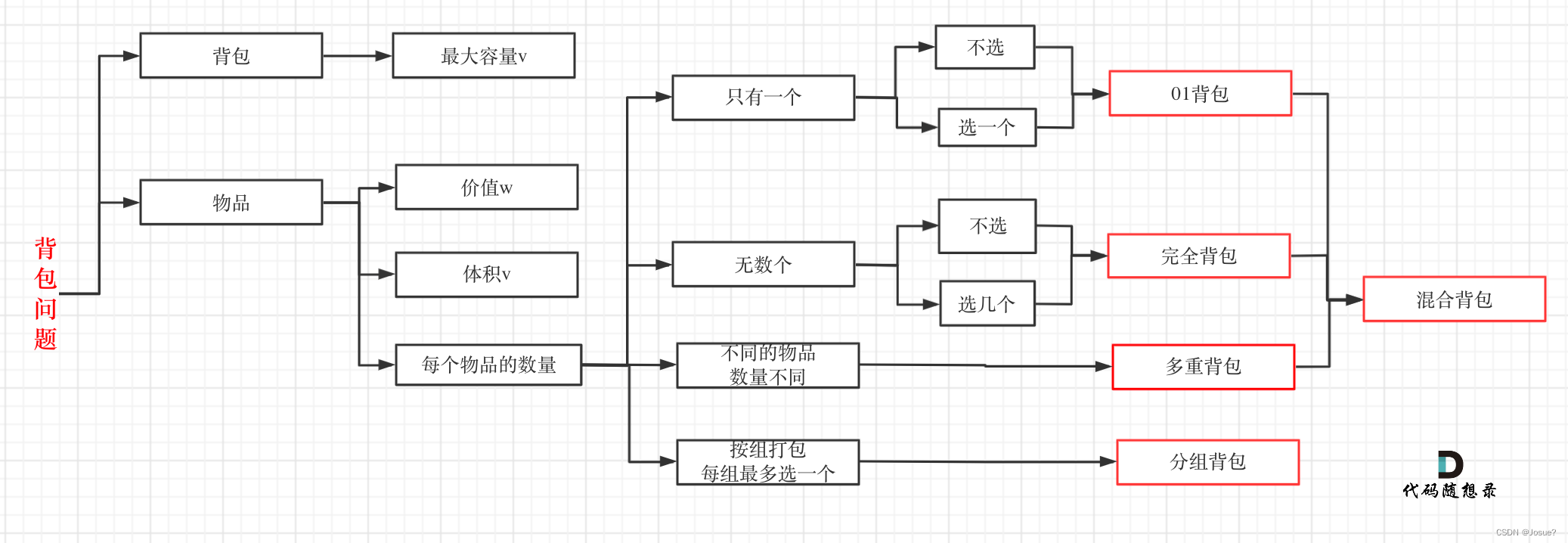
上述内容引用自代码随想录

• 使用动归五部曲分析题目，见过的题目就可以被轻松带走。最重要的就是dp[]数组的含义，递归函数即遍历的顺序。

1.背包递推公式

问能否能装满背包（或者最多装多少）：
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

• 动态规划：416.分割等和子集
• 动态规划：1049.最后一块石头的重量 II
• 动态规划：139.单词拆分

问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：

• 动态规划：494.目标和
• 动态规划：518. 零钱兑换 II
• 动态规划：377.组合总和Ⅳ
• 动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满最大价值：
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

• 动态规划：474.一和零

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

• 动态规划：322.零钱兑换
• 动态规划：279.完全平方数

2.遍历顺序

01背包

二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

完全背包

说完01背包，再看看完全背包。

一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

相关题目如下：

求组合数：

• 动态规划：518.零钱兑换II

求排列数：

• 动态规划：377. 组合总和 Ⅳ
• 动态规划：70. 爬楼梯进阶版（完全背包）

如果求最小数，那么两层for循环的先后顺序就无所谓了，相关题目如下：
求最小数：

• 动态规划：322. 零钱兑换
• 动态规划：279.完全平方数

对于背包问题，其实递推公式算是容易的，难是难在遍历顺序上，如果把遍历顺序搞透，才算是真正理解了。

---

学习时间：

• 上午两个半小时，整理文档半小时。